大跨隔震结构基于结构随机因子法的响应分析

王曙光， 杜东升， 李威威， 缪卓君

(南京工业大学 土木工程学院，南京 211816)

大跨隔震结构基于结构随机因子法的响应分析

王曙光， 杜东升， 李威威， 缪卓君

(南京工业大学 土木工程学院，南京 211816)

结合等价线性化方法，将随机因子法拓展应用到非线性多自由度结构中。选取隔震支座的屈服位移、面积、面压和高度等四个参数为随机变量来考虑隔震层刚度和结构质量的随机性，采用结构随机因子法建立大跨隔震结构的四个随机变量与结构刚度和质量之间的关系，应用代数综合法推导了结构位移响应的数字特征计算表达式。最后通过算例研究了多维地震下大跨隔震结构中结构随机性对位移响应的影响，并获得了一些有意义的结论。

大跨隔震结构；随机因子法；位移响应

隔震技术在大跨结构中的应用越来越广泛，大跨隔震结构的地震反应分析方法[1]，尤其是随机地震反应分析的方法[2-3]，已经成为当前的研究热点。目前的随机性研究大都针对地震动的随机性进行研究，忽略了结构自身随机性的影响。隔震支座力学特性的离散性较其它构件要大，这必然会影响大跨隔震结构地震反应的随机性，因此有必要研究隔震支座随机性对大跨结构随机响应的影响。

本文以随机因子法[4-5]为基础，结合等价线性化方法，将随机因子法拓展应用到非线性多自由度结构中，同时针对隔震结构，选取了隔震支座的屈服位移、面积、面压和高度四个参数来考虑隔震层刚度和结构质量的随机性，研究在多维地震作用下隔震结构隔震支座随机性对结构位移响应的影响。

1 隔震结构的等价线性化方法

多年来，学者们不断提出并完善了一些用来分析滞变结构地震反应的方法，但更高效精确的方法尚在研究阶段。随机分析相较于确定性分析所需要的样本量多，计算总量大，因此本文采用应用广泛、计算效率较高且可避免较大误差的等价线性化方法。

通过曲哲等[6]提出的割线刚度模型得到隔震支座等价刚度如式(1)所示。

(1)

式中：keq和kl分别为等价刚度和初始刚度；μ为延性系数，即最大位移与屈服位移之比；β为屈服后刚度系数，α为屈服后的刚度与初始刚度之比。δ2为支座达到过的最大位移，本文中支座对应的最大位移取弹塑性时程分析中隔震层的平均最大位移。这就建立了支座屈服位移与等价刚度之间的关系，并将该等价线性化模型的地震峰值响应作为原非线性模型的近似。

2 隔震结构的随机因子法

结构随机因子法(RFM)的主要过程如下：首先，将具有不确定性的结构参数变量表示为一个随机因子乘以该结构参数的确定性值。然后，将该结构的质量矩阵和刚度矩阵也分别表示为对应的随机因子乘以其确定性值。最后，可以得到由这些随机因子组成的结构动力特性表达式。由此得到结构参数的随机性对固有频率和振型的影响。该方法主要用于分析材料和几何特性的随机性对结构动力特性的影响。与其他方法相比，结构随机因子法大大降低了所需的计算量。

2.1 隔震层的质量和刚度矩阵

假设大跨隔震结构的隔震层有m个支座。隔震支座在全局坐标下的刚度矩阵[Ke]和质量矩阵[Me]可表示为[7]

(2)

[Me]=Aeae[I]

(3)

式中：Ae，he，μ分别为隔震支座的面积、高度和泊松比；ae为隔震支座的面压；[I]为一个6阶单位矩阵，[T]是一个不包含结构参数6阶方阵。

2.2 随机因子和变异系数

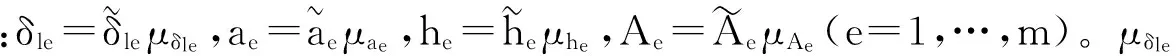
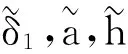
(4)

(5)

同样可以得到第e个支座的质量矩阵为：

(6)

复杂结构的质量矩阵和刚度矩阵可以从有限元软件SAP2000中调取。将支座连接单元的质量和刚度都设为0，运行模态分析后，程序自动会生成不含支座单元质量和单元刚度的结构整体刚度矩阵[Kq]和质量矩阵[Mq]。由于SAP2000在形成刚度矩阵和质量矩阵时，将构件的质量和刚度凝聚在节点上[8]，故需将质量矩阵[Me]和按照等效线性化方法得到的支座等价刚度矩阵[Keq]分别重新加回到整体刚度矩阵和质量矩阵对应节点位置，即可得到完整的结构整体刚度矩阵[K]和质量矩阵[M]。结构阻尼采用经典的Rayleigh阻尼。

2.3 多维地震激励

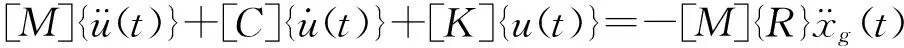
(7)

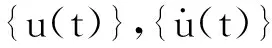
2.4 随机结构的地震响应分析

根据振型分析理论，振型矩阵具有如下正交特性：

[φ]T[M][φ]=[I]

(8)

[φ]T[K][φ]=[Ω]=diag[ω2]

(9)

式(6)和(7)可写为

(10)

(11)

比较式(9)和式(10)，振型的随机变量因子可以写为

(12)

由式(11)，并通过代数综合法[11]可以得到振型φij的平均值μφij、标准差σφij和相应的变异系数：

(13)

(14)

υφij=σφij/μφij

(15)

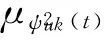
(16)

k=1,2,…，n

(17)

其中

(18)

(19)

其中，σ[M]是由一个与质量矩阵大小一样的零矩阵在对应位置加上σ[Me]得到的。

3 算例

根据上述计算方法，在MATLAB中编写了随机大跨隔震结构位移响应的计算程序，并对图1所示的30m×60m的多点支撑平板网架结构采用李杰等[13]提出的随机地震动模型及建议参数进行了分析，计算截断频率取50Hz。该网架形式为正放四角锥，节点构造型式为焊接空心球节点。第一层柱距为7.5m层高3.6m，第二层层高5.6m，网架高2m。杆件材料为Q235。该大跨隔震结构的设防烈度为8度(0.3g)，Ⅱ类场地。

为了了解大跨隔震结构的动力特性，本文采用通用计算软件SAP2000对其进行模态分析，其中前10阶自振周期与质量参与系数见表1。

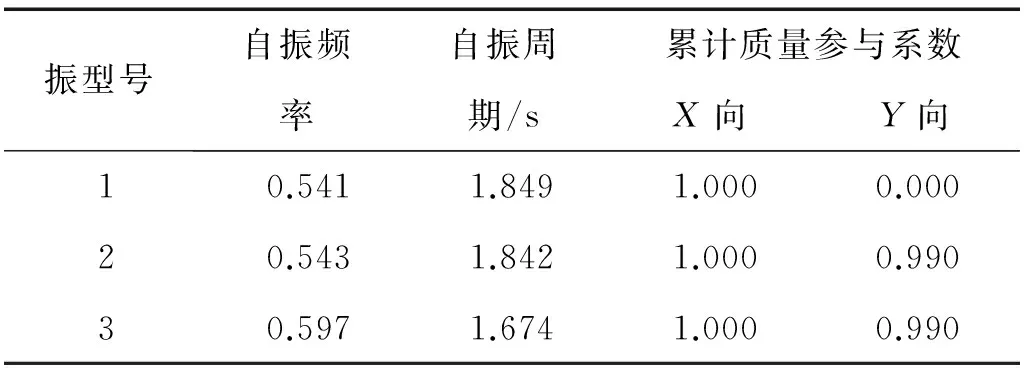
表1 模型自振周期及质量参与系数

该结构的基本周期为1.849 s，结构前2阶振型的累计质量参与系数就已经都超过了95%，反映出结构以平动为主，且X向与Y向刚度接近。

为了考察隔震层各参数随机性对结构动力位移响应的影响，通过多种组合来比较隔震支座屈服位移δl、面压a、高度h和面积A四个因素的变异系数大小对结构位移响应产生的不同影响，具体工况见表2。图2和图3分别列出了相应工况下顶层和隔震层在长边方向的位移响应均方值的变异系数。

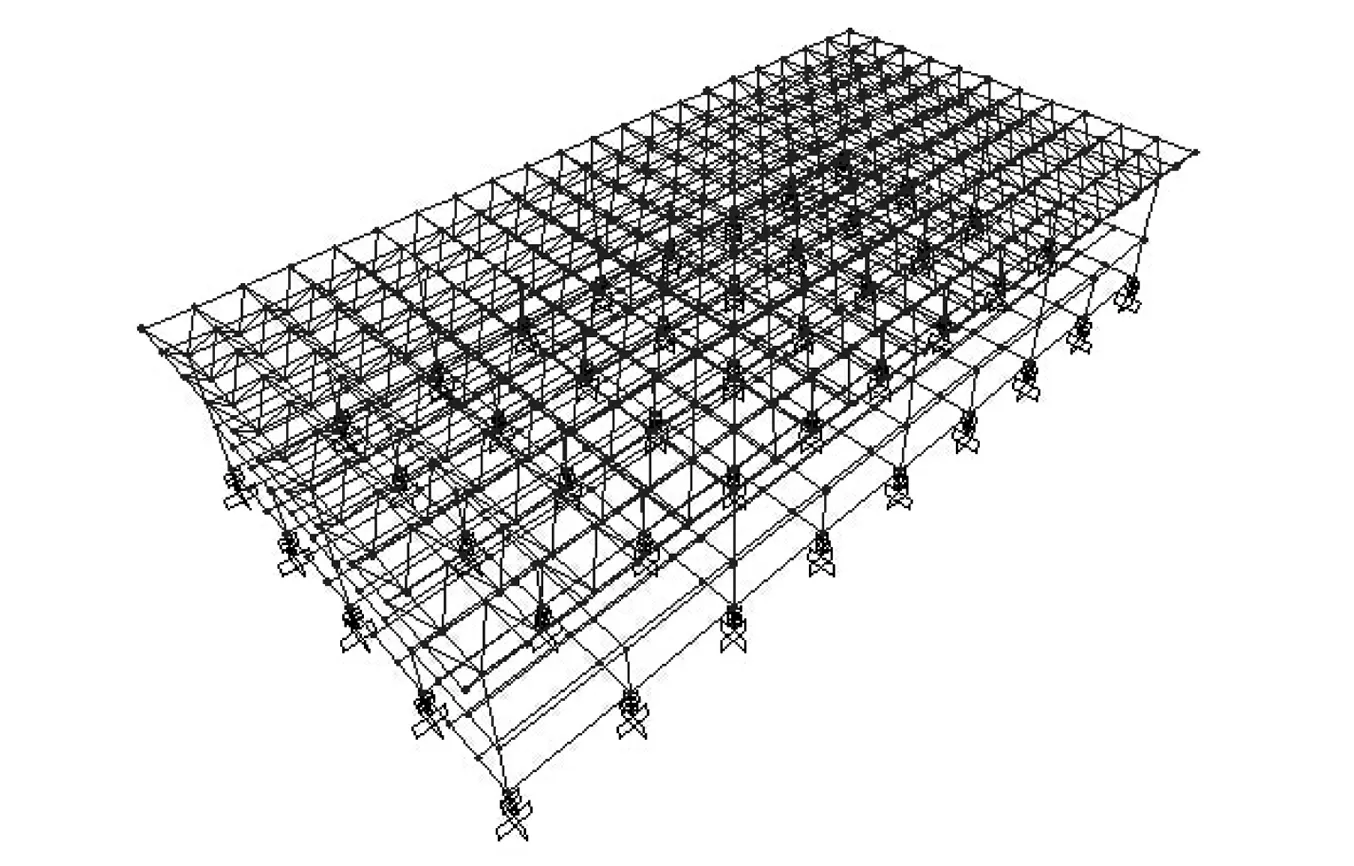
图1 结构示意图Fig.1 Three-dimensional view of the structure

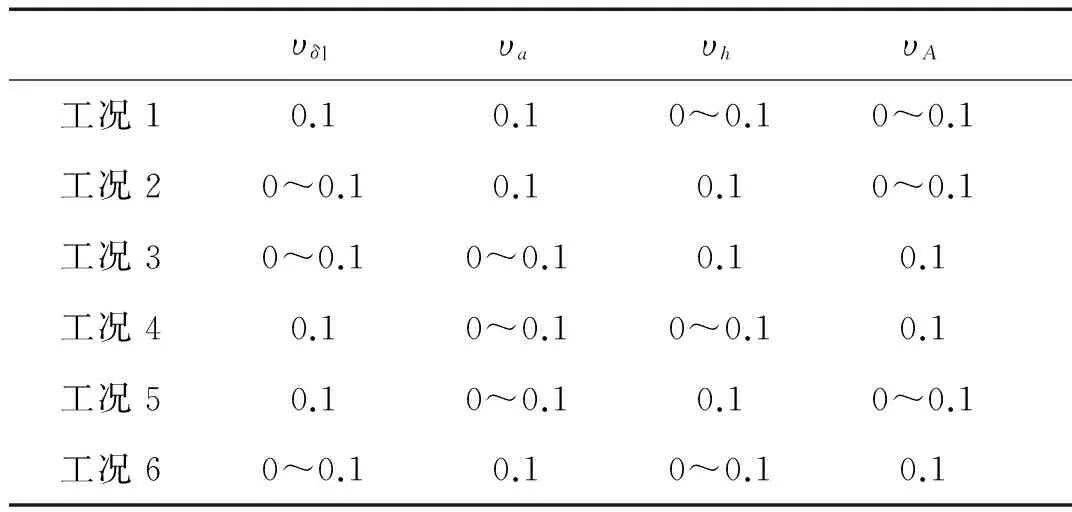
υδlυaυhυA工况10.10.10～0.10～0.1工况20～0.10.10.10～0.1工况30～0.10～0.10.10.1工况40.10～0.10～0.10.1工况50.10～0.10.10～0.1工况60～0.10.10～0.10.1

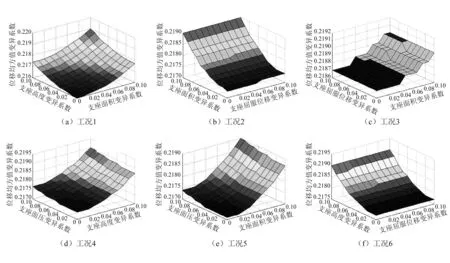
图2 隔震层位移变异系数Fig.2 Variation coefficients of displacements of the isolation layer

通过对比图2中各工况下两个因素对位移变异系数的影响大小，结果显示支座面积变异性对位移响应的影响稍大于支座高度的影响，支座面压变异性的影响大于屈服位移对位移响应的影响即上部结构质量的影响稍大于屈服位移的影响。同时可以看出支座面积和支座高度的变异性对位移响应的影响要明显大于支座面压和支座屈服位移的影响。通过对比各因素对响应影响的变化区间可以进一步得到支座面积和支座高度的影响大约是支座面压和支座屈服位移的4倍～5倍。

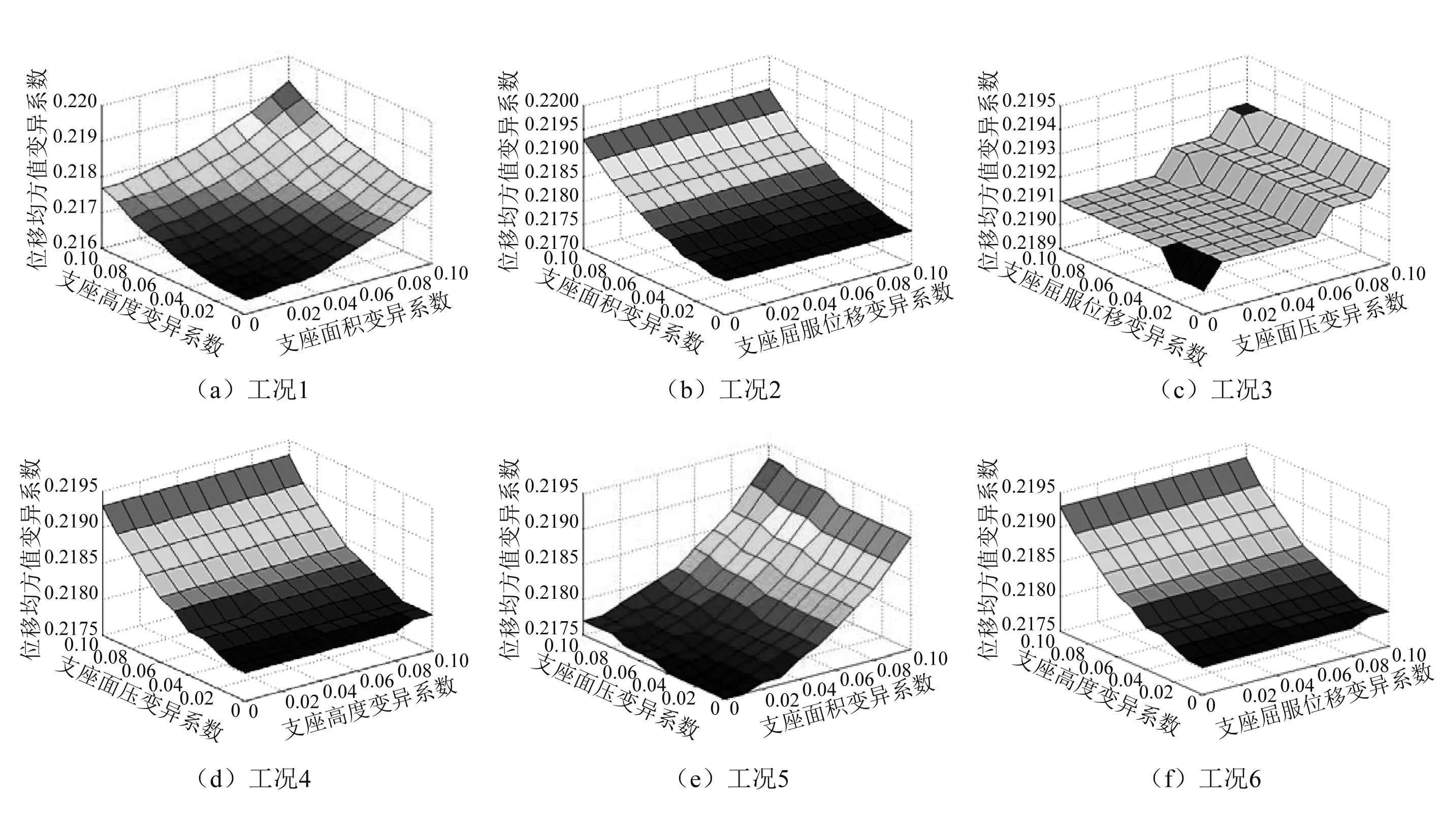
图3 顶层位移变异系数Fig.3 Variation coefficients of displacements of the top floor

通过对比图3中各工况下两个因素对位移变异系数的影响大小，结果显示支座面积和高度对位移响应的影响大于支座屈服位移和面压的影响。通过对比各因素对响应影响的变化区间可以进一步得到支座面积和支座高度的影响大约是支座面压和支座屈服位移的8倍～10倍。

将结构顶层位移响应与隔震层的相应计算结果进行对比后可以看出，由隔震层四个因素引起的结构变异性对隔震层位移响应的影响要略小于对结构顶层的影响。

4 结 论

(1)隔震支座的屈服位移(δle)、面压(ae)和几何尺寸(he，Ae)对结构位移响应均方值离散性的影响程度是不同的。

(2)支座面积变异性对位移响应的影响稍大于支座高度的影响，支座面压变异性的影响稍大于屈服位移对位移响应的影响即上部结构质量的影响稍大于屈服位移的影响。支座面积和支座高度的变异性对位移响应的影响要明显大于支座面压和支座屈服位移的影响，在生产隔震垫时应对支座面积和高度的误差控制给予足够的重视。

(3)随着隔震支座各参数的变异系数增大，结构位移响应均方值的离散性亦增大。

[1] 曹资,薛素铎.空间结构抗震理论与设计[M].北京: 科学出版社,2006.

[2] 刘章军,雷耀龙,方兴. 大跨桥梁结构随机地震反应的概率密度演化分析[J]. 土木工程学报,2013(增刊1):226-232. LIU Zhangjun, LEI Yaolong, FANG Xing. Probability density evolution method-based random seismic response analysis of cable-stayed bridges [J]. China Civil Engineering Journal, 2013(Sup1):226-232.

[3] 彭勇波，李杰.非线性时变结构随机地震响应最优多项式控制[J].振动与冲击,2016,35(1):210-215. PENG Yongbo,LI Jie.Optimal polynomial control for random seismic response of non-linear time-varying[J]. Journal of Vibration and Shock,2016,35(1):210-215.

[4] GAO Wei. Random seismic response analysis of truss structures with uncertain parameters[J]. Engineering Structures, 2007, 29(7)：1487-1498.

[5] 高伟,陈建军,程怡,等. 随机刚架结构在平稳随机激励下的动力响应分析[J]. 振动与冲击,2004,23(2):89-91. GAO Wei, CHEN Jianjun, CHENG Yi,et al. Dynamic response analysis of stochastic rigid structures under stationary random excitation[J]. Journal of Vibration and Shock,2004,23(2):89-91.

[6] 曲哲,叶列平. 计算结构非线性地震峰值响应的等价线性化模型[J]. 工程力学,2011,28(10):93-100. QU Zhe, YE Lieping. An equivalent linear modal to estimate maximum inelastic seismic responses ofstructural systems [J]. Engineering Mechanics, 2011,28(10):93-100.

[7] 周锡元,马东辉,曾德民,等. 隔震橡胶支座水平刚度系数的实用计算方法[J]. 建筑科学,1998(6):3-8. ZHOU Xiyuan, MA Donghui, ZENG Demin,et al.A practical computation method for horizontal rigidity coefficient of seismic isolation rubber bearing [J]. Building Science, 1998(6):3-8.

[8] 北京金土木软件技术有限公司.SAP2000中文版使用指南[M].北京:人民交通出版社,2006.

[9] LI Q S, ZHANG Y H, WU J R, et al.Seismic random vibration analysis of tall buildings [J] Engineering Structures,2004,26(12):1767-1778.

[10] 建筑抗震设计规范：GB 50011—2010[S].北京:中国建筑工业出版社,2010.

[11] 陈建军. 机械与结构系统的可靠性[M]. 西安:西安电子科技大学出版社,1994.

[12] GAO W, CHEN J J, CUI M T, et al. Dynamic response analysis of linear stochastic truss structures under stationary random excitation [J]. Journal of Sound and Vibration,2005,281(1/2):311-321.

[13] 李杰,艾晓秋. 基于物理的随机地震动模型研究[J]. 地震工程及工程振动,2006(10):21-26. LI Jie, Ai Xiaoqiu. Study on random model of earthquake ground motion based on physical process [J]. Earthquake Engineering and Engineering Vibration, 2006(10):21-26.

Response analysis of large-span isolated structures based on the random factor method

WANG Shuguang, DU Dongsheng, LI Weiwei, MIAO Zhuojun

(School of Civil Engineering, Nanjing Tech University, Nanjing 211816，China)

Combined with the equivalent linearization technique, the random factor method was applied to analyse multi-degree-of-freedom nonlinear isolated structures. Four random factor, namely the yield displacement, area, pressure and height of the isolation bearing were chosen to consider the randomness of isolation layer stiffness and structural mass. The relationships between the four basic random variables and the structural stiffness and mass were established by using the method provided. The computational expressions of the structural displacement response were deduced by using the algebra synthetic method. Then a long-span isolated structure was analysed based on the improved random factor method and some beneficial conclusions were obtained.

large-span isolated structures; random factor method; displacement response

国家自然科学基金(51678301；51678302)；江苏省产学研前瞻性联合研究项目(BY2015005-14)

2015-08-28 修改稿收到日期：2016-03-10

王曙光 男，博士生导师，1972年生 E-mail: 720108@vip.sina.com

TU352.1

A

10.13465/j.cnki.jvs.2017.10.025