含液饱和不可压多孔弹性板的随机振动

周凤玺, 李 丹, 曹小林

(1.兰州理工大学 土木工程学院，兰州 730050； 2.西部土木工程防灾减灾教育部工程研究中心，兰州 730050)

含液饱和不可压多孔弹性板的随机振动

周凤玺1,2, 李 丹1, 曹小林1

(1.兰州理工大学 土木工程学院，兰州 730050； 2.西部土木工程防灾减灾教育部工程研究中心，兰州 730050)

在不可压多孔弹性介质理论和随机振动理论的基础上，以Kirchhoff假定和小变形为前提，根据饱和不可压多孔板弯曲的数学模型，针对孔隙流体沿面内扩散的情形，建立了含液饱和多孔弹性板在集中荷载作用下横向弯曲的随机振动方程。针对四边简支矩形板，对板内位移响应和截面固相弯矩响应进行了分析，分别得到了输入集中荷载为平稳随机过程时简支板的位移响应和弯矩响应的功率谱密度函数和方差等数字特征。作为数值算例，考虑一理想白噪声平稳随机集中荷载作用下的简支饱和多孔板，对其位移响应和界面固相弯矩的功率谱密度函数进行了分析，并讨论了流-固耦合项对板位移以及弯矩的影响规律。结果表明，通过调整孔隙中流体的渗透系数可以达到控制板随机振动的目的。

多孔介质理论；随机振动；功率谱密度函数；四边简支板

多孔介质理论假设多孔介质理想化地分布在整个区域中,但每一相物粒子拥有各自独立的运动,在连续介质混合物公理和体积分数限制下建立相应的基本方程,充分考虑其中流体、固体骨架的应力应变关系，若干微观性质直接通过宏观性质描述,不仅避免了Biot理论模型中的非相容量和杂交混合物理论中的繁杂公式,而且更加符合连续介质力学理论体系[1-3]。在不需要额外的假定下,诸如动力、材料和几何非线性等一些效应可直接反映在其数学模型中。近年来，基于连续介质混合物公理和体积分数概念的多孔介质理论的理论和数值方法研究都已取得了长足的进展，并广泛地应用于不同工程领域中。但大多数的研究主要是几何特征为为无限半空间域或有限厚度层的岩土类材料，以大型实体物为主，对于小型柔韧方面，如多孔介质梁、板等结构研究则相对较少，而且多孔介质理论研究柔韧多孔结构力学行为主要关注生物力学和传热传质学等中的若干实际问题[4-5]，如对软骨组织以及植物的茎杆和热交换管道等的力学分析，但是复合多孔材料已广泛应用于建筑、汽车和航空等不同行业中，如用于减震和吸音的聚亚安酯泡沫塑料和纤维材料[6-7]，因此，有必要对多孔柔韧结构动静力行为进行深入的分析。

目前应用多孔介质理论对饱和多孔弹性结构力学行为的研究成果中,杨骁等人分别建立了饱和不可压多孔弹性梁轴向扩散下的线性和非线性动力响应数学模型,通过Laplace变换法和Galerkin法研究了饱和不可压多孔弹性梁的动力和拟静定弯曲问题[8]。周凤玺等人基于线弹性理论和 Biot 多孔介质模型，分析了含液饱和多孔二维简支梁的动力响应，其中考虑了固体颗粒和流体的可压缩性以及孔隙流体的黏滞性。通过 Fourier 级数展开和常微分方程组的求解，得到了含液饱和多孔二维梁动力响应问题的解[9-10],以及根据不可压多孔弹性介质理论和随机振动理论，建立了孔隙流体沿轴向扩散的情形下，含液饱和多孔弹性梁在集中荷载作用下横向弯曲的随机振动方程。对梁的位移响应和截面固相弯矩响应进行分析，分别得到了输入集中荷载为平稳随机过程时简支梁的位移响应和弯矩响应的功率谱密度函数和方差等数字特征[11]。薛开等人采用改进傅里叶级数的方法对任意弹性边界条件下的单向变厚度薄板进行自由振动分析，将板的振动位移函数表示为标准的二维傅里叶余弦级数和辅助级数的线性组合。通过辅助级数的引入，解决了位移导数在边界不连续的问题[12-13]。何录武等研究了饱和不可压多孔弹性板在面内扩散下的动力弯曲理论[14]。基于不可压多孔介质理论，在Kirchhoff假定和小变形前提下，针对流体的面内扩散情形，建立了饱和不可压多孔弹性板动力弯曲的数学模型，利用Fourier展开法研究分析了阶梯载荷作用下四边简支透水矩形多孔弹性板的拟静定和动力弯曲响应[15-16]。

当结构受到外界的随机激励时，它就有可能发生随机振动，其危害性给人们的日常生活带来很大的困扰，因此，对有关结构或构件的随机振动的研究已取得了一系列研究成果[17-19]，但是关于含液饱和多孔材料结构的随机振动分析，目前见之甚少。本文根据不可压饱和多孔介质模型和连续体的随机振动理论，以简支板为例，研究了不可压含液饱和弹性板在随机集中荷载作用下的随机振动。对板的挠度响应以及界面固相弯矩响应进行了分析，获得了功率谱密度函数、方差等数字特征，重点分析了流-固耦合项对板减振效果的影响规律。

1 含液饱和多孔板的随机反应

含液饱和多孔板属于两相多孔介质，是由多孔固体骨架和充填液体构成，用角标α表示固体骨架(α=s)和充填液体(α=f)的相关物理量。如图1所示的含液饱和多孔板，在(xp,yp)处受到一个集中随机荷载p(t)的作用。在假设结构本身内阻尼力与应变速度成正比的情形下，考虑孔隙流体仅沿面内扩散，引入组分不可压假设，可得到含液饱和多孔板的运动微分方程为构成面内扩散情形下饱和不可压多孔弹性板的基本控制方程

(1)

(2)

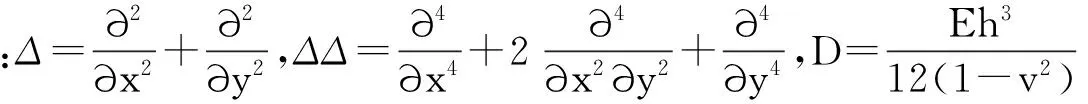
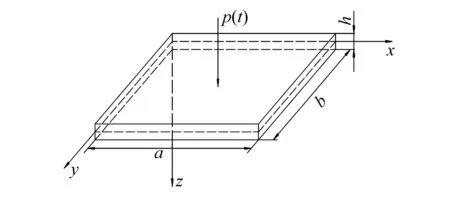
图1 弹性地基上的饱和多孔板Fig.1 A saturated poroelastic plate on elastic foundation

设第(m,n)阶主振动挠度为

wmn(x,y,t)=φmn(x,y)Amn(t)

则含液饱和多孔板的挠度w(x,y,t)为

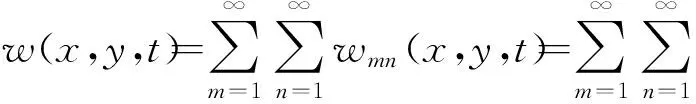
(3)

其中φ(x,y)表示(m,n)阶振型函数且为坐标变量，Amn(t)为时间变量。

对于四边简支矩形板，其边界条件：

满足上述边界条件且函数序列在函数空间中线性无关,则振型函数可取为

(4)

其中，m,n均为正整数。

将式(3)和式(4)分别代入式(1)和式(2)中，然后用第(i,j)个振型函数φij(x,y)同乘等式两边，并沿板面进行积分，利用固有振型的正交条件和Dirac函数性质可得

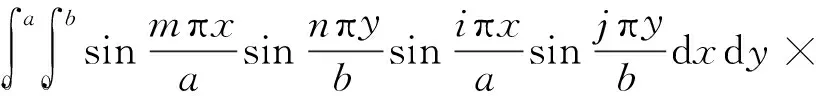
(5)

当m≠i,n≠j时，上式为0

当m=i,n=j时，上式变为

(6)

第(m,n)阶简支板的固有频率为

(7)

将式(7)代入式(6)，可得

(8)

式中，ξn为含液饱和多孔板的内阻尼率，且有

(9)

由式(8)，可以得到主坐标Amn(t)对应于输入为集中荷载p(t)时的频响函数

(10)

结合式(3)，根据叠加原理可得到含液饱和多孔板的第(m,n)阶主阵型Amn(x,y,t)频响函数为

(11)

通过式(11)可以获得板的脉响函数以及板的动力响应。

2 随机反应的统计值

2.1 挠度的功率谱密度以及均方值

考虑饱和不可压板上的集中荷载p(t)是均值为零、谱密度为Sp(ω)的平稳随机过程，则第(m,n)阶主振动wmn(x,y,t)的谱密度为

(12)

从式(12)可以看出，Swmn分别与板的长、宽和厚度的二次方成反比；当饱和多孔板的阻尼系数ξn较小,且Sp(ω)为白噪声时,在固有频率ωmn附近出现共振，此时Swmn与固有频率ωmn的四次方成反比,因此可以得出高阶挠度分量的功率谱密度较小；在板上位置不同的各点,挠度分量的功率谱密度随着点位置的不同而变化,但在板边缘处始终为零。

由于固有阵型函数序列在函数空间中线性无关,wmn(x,y,t)(m,n=1,2,…)可以视为不相关，挠度w(x,y,t)的功率谱Sw(x,y,ω)为各个挠度分量的功率谱Swmn(x,y,ω)密度的叠加，即有：

(13)

当输入p(t)为理想白噪声时，即Sp(ω)为一常数Sp，求响应的方差就变为计算频率响应函数幅值平方的积分，则通过留数积分可求得任意(m,n)阶挠度wmn(x,y,t)方差为

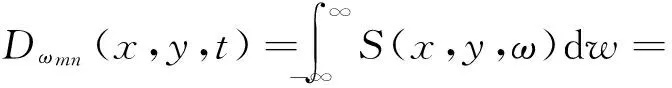
(14)

由于固相和流相的耦合系数Sv与Darcy渗透系数kf成反比，结合式(9)和式(15)可以发现，随着饱和多孔板的渗透系数kf减小挠度分量的方差也随之减小；挠度分量方差与固有频率ωmn的三次方成反比,所以高阶挠度分量的方差较小；由于饱和多孔板中流-固耦合引起的内阻尼与固有振型的阶数无关,因此流-固耦合引起的内阻尼对减小各阶挠度分量的方差具有同样的效果,这就使得含液饱和结构特别适用于减小多频或宽带随机激励下振动；随着多孔板上位置的不同,各点的挠度分量方差不同，在固有振型的边缘处,方差始终为零。

挠度w(x,t)的方差为

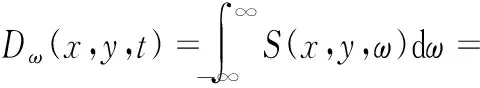
(15)

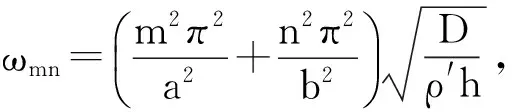
(16)

由式(9)和式(16)可知，在含液饱和板中，流体在孔隙中的渗透系数对流-固耦合引起的减振效果影响较大，而流体的体积分数nf对其影响可以忽略不计。

2.2 固相弯矩的功率谱密度及方差

结合式(3)，由不可压饱和多孔板的本构关系得固相弯矩M(x,y,t)为

(17)

当输入p(t)是均值为零、谱密度为Sp(ω)的平稳随机过程时，板固相弯矩Mx、My、Mxy的功率谱密度与板挠度的功率谱密度相似，即：

(18)

(19)

(20)

当集中荷载p(t)为理想白噪声时，固相弯矩Mx,My,Mxy的方差为

(21)

(22)

(23)

从上式看出，随着渗透系数kf减小，饱和多孔板的弯矩方差也降低，与对板挠度的影响相似。

因此，设单相弹性固体板截面弯矩M0的方差为DM0，则单相弹性板和不可压饱和板的截面弯矩的方差比为βM=DM/DM0，可以得到

(24)

(25)

(26)

由式(9)、(24)～(26)可知，得出相似结论，在含液饱和板中，流体在孔隙中的渗透系数对流-固耦合引起的减振效果影响起决定性作用，不计流体的体积分数nf对其的影响。

3 数值算例

选取饱和多孔不可压四边简支方板，板长l=1 m，h=0.1 m,饱和多孔材料的物理力学参数为E=8.375×106N/m2，v=0.3，C=0.02 s，nf=0.33，ρs=2 000 N/m3，ρf=330 N/m3,γRf=1.0×104N/m3,kf=5×10-2～5×10-5m/s。在集中荷载为平稳随机过程下，且为理想白噪声时，其功率谱密度为常数Sp。

在图2～图5中，分别绘出了随机集中荷载作用在板中点(1/2,1/2)，kf=5×10-2～1×10-3m/s不同渗透系数下，板的中点位移以及截面弯矩的功率谱密度函数Sw/Sp与频率的关系曲线。功率谱密度函数图形从频域方面描述振动的统计特性，反映振动能量对频率的分布规律。由图2～图4可以看出，在饱和多孔板中流-固耦合项作用下，单相弹性介质与不同渗透系数下的位移响应和弯矩响应功率谱随频率ω的变化曲线明显不同；随着孔隙中流体渗透系数kf的逐渐增加，功率谱随频率ω的增大而减小，功率谱的变化速率不断减小；单相介质弹性板与之相反，功率谱随频率ω的增大而增大，功率谱的变化速率不断增大；利用此性质可通过改变流体的渗透系数来改变振动能量对频率的分布规律。但在图5中，饱和多孔板功率谱的形状与单相连续弹性板相似,在薄板中，Mxy由剪切力τxy引起的合力矩，在多孔介质中，孔隙流体不传递剪应力，因此其功率谱的变化速率同单相弹性板基本相同，随着频率ω的增大，变化速率不断增大。

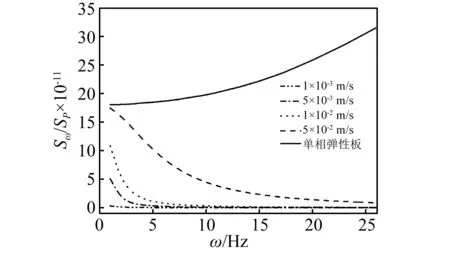
图2 板中点位移响应功率谱密度函数Fig.2 Power spectral density function of the plate midpoint displacement response

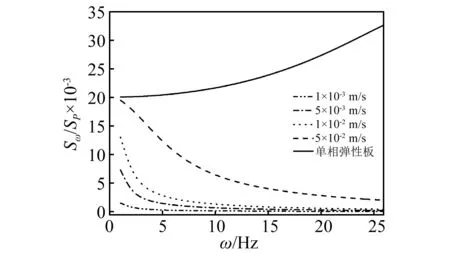
图3 板中截面X方向弯矩响应功率谱密度函数Fig.3 Power spectral density function of the plate bending moment response in the X -direction

图4 板中截面Y方向弯矩响应功率谱密度函数Fig.4 Power spectral density function of the plate bending moment response in the Y -direction

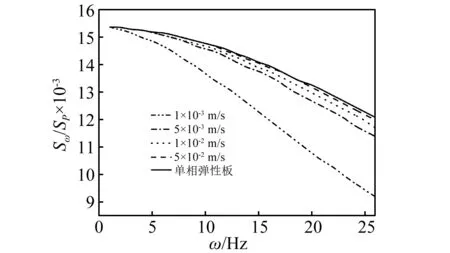
图5 板中截面扭矩响应功率谱密度函数Fig.5 Power spectral density function of the cross section of the plate in the cross section

为了分析含液饱和板中流-固耦合引起的阻尼对板的挠度和弯矩的减振效果，在图6～图9中，分别绘出了βw和βM随渗透系数的变化曲线。从图中可以看出，

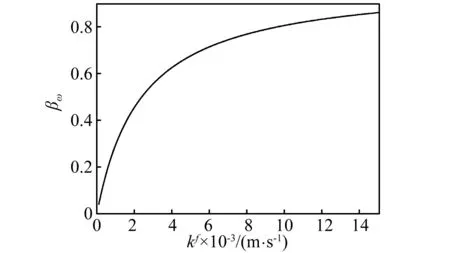
图6 板的βw与kf关系曲线Fig.6 Relationship curve of βw and kf of the plate

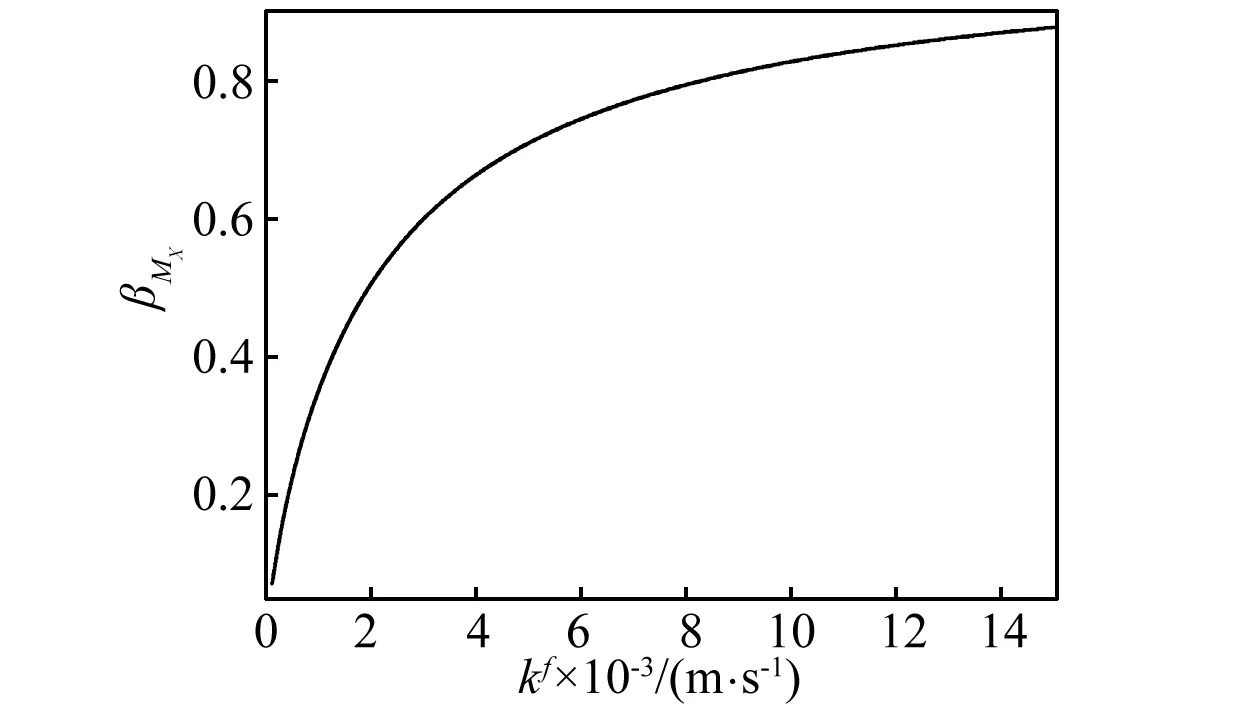
图7 板的βMX与kf关系曲线Fig.7 Relationship curve of βMX and kf of the plate

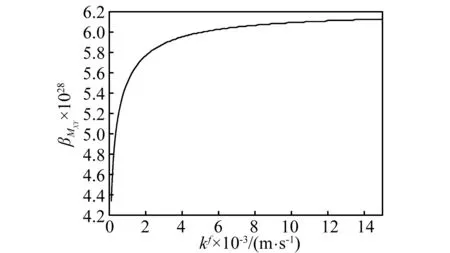
图8 板的βMXY与kf关系曲线Fig.8 Relationship curve of βMXY and kf of the plate

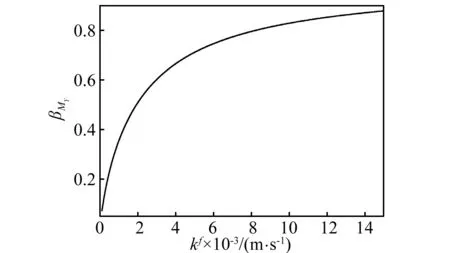
图9 板的βMY与kf关系曲线Fig.9 Relationship curve of βMY and kf of the plate

当渗透系数kf比较小时，βw和βM较小, 之后，在一定范围内随着kf的增大不断增大，说明这时减振比较有效；当kf增大到一定程度时, 曲线趋于平缓, 说明这时再增大kf对减振效果不大。利用此性质可以通过控制渗透系数kf的大小来调节含液饱和板中流-固耦合引起的阻尼对板的挠度和弯矩的减振效果，进而在结构减振降噪方面发挥重要作用。

为了讨论含液饱和板长宽比对板位移与弯矩功率谱密度的影响。在不同的长宽比下，图10和图11分别绘出了板位移功率谱密度以及板弯矩功率谱密度随频率的变化曲线，并与饱和多孔弹性梁进行了比较。从图中可以看出，长宽比对简支板的位移响应和弯矩响应的功率谱密度有着显著的影响，可通过改变板的长宽比来改变振动能量对频率的分布规律，且当长宽比越小时，其响应越接近于饱和弹性梁。

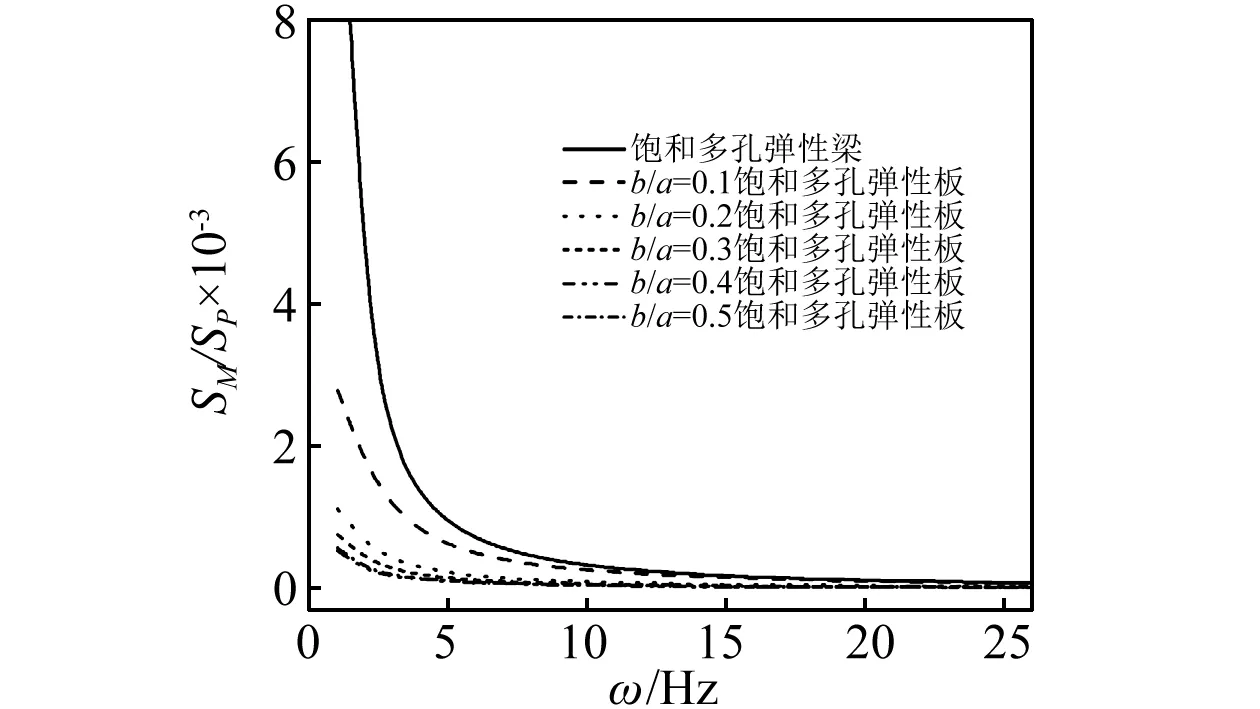
图10 不同长宽比时弯矩响应功率谱密度函数Fig.10 Power spectral density function with difference length-width ratio

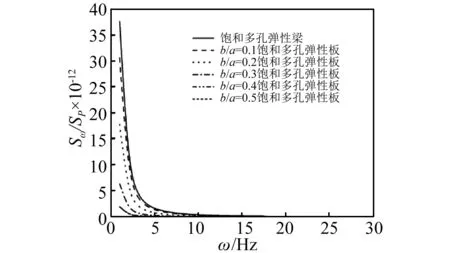
图11 不同长宽比时位移响应功率谱密度函数Fig.11 Power spectral density function with difference length-width ratio

4 结 论

在不可压饱和多孔介质模型和随机振动理论的基础上，研究了不可压含液饱和弹性简支板在随机集中荷载作用下的随机振动。分析结果表明：

(1)在饱和多孔板中流-固耦合项作用下，随kf的增加挠度和弯矩响应谱的值随频率的增加而变小，且与单向介质弹性板的变化趋势相反，因此通过调节孔隙中流体的渗透系数kf的值来改变振动能量对频率的分布规律。且在多孔介质中，孔隙流体不传递剪应力，因此其功率谱的变化速率同单相弹性板基本相同，因此不能改变振动能量对频率的分布规律。

(2)孔隙中流体的渗透系数的减小可以增大含液饱和板的阻尼系数ξn，挠度和弯矩方差减小，βw和βM随之减小，减振效果显著，但超过一定范围，随着渗透系数增大，βw和βM变化趋于平缓，减振效果就不显著了。

(3)当板的长宽比越小时，板的弯矩和位移功率谱密度越接近饱和弹性梁的响应。

(4)对各阶固有振型，流-固耦合项有同样的减振效果，因此流-固耦合阻尼减振特别适用于弹性板在多频或宽带随带激励的情况。

[1] DE BOER R. Reflections on the development of the theory of porous media[J]. Applied Mechanics Review, 2003, 56(6): 94-97.

[2] BOWEN R M. Incompressible porous media models by use of the theory of mixtures[J]. International Journal of Engineering Science，1980, 18: 1129-1148.

[3] BOWEN R M. Compressible porous media models by use of the theory of mixtures[J]. International Journal of Engineering Science, 1982, 20: 697-735.

[4] TABER L A. A theory for transverse deflection of poroelastic plates[J]. ASME Journal of Applied Mechanics, 1992, 59: 628-634.

[5] LI L P, CEDERBAUM G, SCHULGASSER K. Theory of poroelastic plates with in-plane diffusion[J]. International Journal of Solids and Structures, 1997, 34(35/36): 4515-4530.

[6] LECLAIRE P, HOROSHENKOV K V, CUMMINGS A. Transverse vibration of a thin rectangular porous plate saturated by a fluid[J]. Journal of Sound and Vibration, 2001, 247(1): 1-18.

[7] LECLAIRE P, HOROSHENKOV K V, CUMMINGS A. The vibrational response of a clamped rectangular porous plate[J]. Journal of Sound and Vibration, 2001, 247(1): 19-31.

[8] 杨骁,李丽.不可压饱和多孔弹性梁、杆动力响应的数学模型[J]. 固体力学学报,2006, 27(2): 159-166. YANG Xiao, LI Li. Large deflection analysis of simply supported saturated poroelastic beam[J]. Chinese Journal of Solid Mechanics, 2006, 27(2): 159-166.

[9] 周凤玺,马强,宋瑞霞. 含液饱和多孔二维梁的动力特性分析[J].工程力学, 2015, 32(5): 198-207. ZHOU Fengxi, MA Qiang, SONG Ruixia. Dynamic response analysis of a two dimensional fluid-saturated porous beam[J]. Engineering Mechanics, 2015, 32(5):198-207.

[10] 周凤玺,米海珍.弹性地基上不可压含液饱和多孔弹性梁的自由振动[J].兰州理工大学学报，2014, 40(2): 118-122. ZHOU Fengxi, MI Haizhen. Free vibration of poroelastic beam with incompressible saturated liquidmon elastic foundation [J]. Journal of Lanzhou University of Technology, 2014, 40(2): 118-122.

[11] 周凤玺，马强，米海珍.含液饱和多孔弹性梁的随机振动[J].振动与冲击, 2015, 34(22): 206-209. ZHOU Fengxi, MA Qiang, MI Haizhen. Random vibration of fluid-saturated porous elastic beam[J]. Journal of Vibration and Shock , 2015, 34(22): 206-209.

[12] 裴然,杜敬涛,朱明刚，等.弹性板结构面内振动特性分析与实验研究[J].哈尔滨工程大学学报，2015, 36(4): 1-5. Pei Ran, Du Jingtao, Zhu Minggang, et al. In-plane modal characteristics of flexible plate structure and its experimental study[J]. Journal of Harbin Engineering University, 2015, 36(4): 1-5.

[13] 薛开,王久法,王威远，等.变厚度薄板在任意弹性边界条件下的自由振动分析[J].振动与冲击，2013, 32(21): 132-137. XUE Kai, WANG Jiufa, WANG Weiyuan, et al. Free vibration analysis of tapered plates with arbitrary elastic boundary condition[J]. Journal of Vibration and Shock, 2013, 32(21): 132-137.

[14] 李丽，杨骁.简支饱和多孔弹性梁的非线性弯曲[J].力学季刊，2007, 28(1): 86-91. LI Li, YANG Xiao. Nonlinear bending of simply supported saturated poroelastic beam[J]. Chinese Quarterly of Mechanics, 2007, 28(1): 86-91.

[15] 杨骁，程昌钧.流体饱和多孔介质的动力学Gurtin型变分原理和有限元模拟[J].固体力学报，2003, 24(3): 267-276. YANG Xiao, CHENG Changjun. Gurtin variational principle and finite element simulation for dynamical problems of fluid-saturated porous media[J]. Acta Mechanica Solida Sinica, 2003, 24(3): 267-276.

[16] 何录武,杨骁. 饱和不可压多孔弹性板在面内扩散下的动力弯曲理论[J].固体力学学报，2008, 29(2): 121-128. HE Luwu, YANG Xiao. A dynamic bending model of incompressible saturated proelastic plates with in-plane diffusion[J]. Chinese Journal of Solid Mechanics, 2008, 29(2): 121-128.

[17] 欧进萍,王光远.结构随机振动[M]．北京:高等教育出版社，1998.

[18] LIU D, XU W, XU Y. Stochastic response of an axiall moving viscoelastic beam with fractional order constitutive relationand random excitations[J]. Acta Mechanica Sinica, 2013, 29(3): 443-451.

[19] 刘又文.应用固体力学[M].北京:中国科学文化出版社, 2003.

Random vibration of fluid-saturated porous elastic plates

ZHOU Fengxi1,2, LI Dan1, CAO Xiaolin1

(1. School of Civil Engineering, Lanzhou University of Technology, Lanzhou 730050, China;2. Western Engineering Research Center of Disaster Mitigation in Civil Engineering of Ministry of Education, Lanzhou University of Technology, Lanzhou 730050, China)

On the basis of the theories of incompressible porous elastic medium and random vibration, on the premises of Kirchhoff assumption and small deformation, according to the mathematical model for the bending of saturated incompressible porous plates, a random vibration equation for the transverse bending of fluid-saturated porous elastic plates was established with a concentrated load under the condition of in plane diffusion of pore fluid. Through the analysis on the displacement response of plate and the solid phase moment response of cross section, the power spectral density function and the variance as well as other digital features of the displacement and moment responses of a simply supported plate were obtained when the concentrated load is a stationary random process. As a numerical example, the saturated porous simply supported plate under the concentrated load with an ideal white noise stationary randomness was considered, the power spectral density functions of the displacement and moment response were analyzed and the damping effect of the fluid-solid coupling term on the plate displacement and bending moment was discussed. The results show that the random vibration of the plate could be controlled by changing the permeability coefficient of the pore fluid.

porous media theory; random vibration; power spectral density function; simply supported plate

国家自然科学基金(11162008；51368038)；甘肃省环境保护厅(GSEP-2014-23)；甘肃省教育厅研究生导师基金(1103-07)

2015-10-27 修改稿收到日期： 2016-02-27

周凤玺 男，博士，教授，1979年2月生

E-mail：geolut@163.com

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.10.027