随机振动响应下空间相机支撑结构设计与试验

李 林， 王 栋， 孔 林， 谭陆洋， 杨洪波

(1.中国科学院 长春光学精密机械与物理研究所,长春 130033；2.中国科学院大学,北京 100049； 3.长光卫星技术有限公司,长春 130033)

随机振动响应下空间相机支撑结构设计与试验

李 林1，2， 王 栋1,3， 孔 林1,3， 谭陆洋1,2， 杨洪波1

(1.中国科学院 长春光学精密机械与物理研究所,长春 130033；2.中国科学院大学,北京 100049； 3.长光卫星技术有限公司,长春 130033)

针对某高分辨率空间相机结构随机振动加速度响应大的问题，对空间相机支撑结构进行了优化设计。建立了基于随机振动响应分析的数学模型，推导了随机振动均方根响应表达式。基于三点定位原理和双脚架柔性结构原理设计了相机支撑结构，以相机安装点RMS值最小为目标，基频作为约束，建立了相机支撑结构随机响应优化模型，对支撑结构柔性环节位置进行了尺寸优化设计。采用MSC.Patran&Nastran有限元分析软件对优化处理后的支撑结构进行了工程分析，相机安装点随机响应RMS值最大19.6 grms。最后，对相机支撑结构进行了随机振动试验，结果显示,有限元分析结果与试验测量数据符合的较好，最大相对误差为8.2%，所设计的空间相机支撑结构满足空间相机使用要求，验证了所采用优化方法的可行性。

空间相机；支撑结构；随机振动响应；优化设计；功率谱密度

近高分辨对地观测技术是当前空间技术发展的一个重要方向，在运载火箭升空的主动段，卫星平台受到火箭的脉动推力、喷气噪声以及紊流边界层噪声等综合产生的随机振动激励[1]。通过卫星平台与空间相机连接的相机底部支撑结构，这些环境激励直接从相机支撑结构传递到相机结构上，将引起相机结构变形甚至破坏相机结构。计算在随机载荷作用下相机支撑结构的响应，根据随机载荷响应进行结构设计是卫星结构设计中的重要任务。

随着空间技术的发展，逐渐形成了卫星随机振动环境下结构强度的设计方法，并应用于实际工程项目中。张军等[2]通过对卫星结构加速度响应的均方根值、累积均方值和功率谱密度等统计量的分析，研究了随机振动试验中卫星结构的随机响应，以此考察了卫星承受随机载荷的能力。杨新峰等[3]提出了地面随机振动响应与板面密度关系的一个经验公式，探讨了某小卫星主动段振动特性与地面试验的振动特性差异，给出了修正地面试验验证的一些建议。张玉梅等[4]介绍了3种随机振动环境等效原则的基本原理、处理方法，在综合分析的基础上推荐使用基于位移和应力峰值响应等效的设计方法。

本文针对某卫星结构设计要求，综合某高分辨率空间相机性能条件，基于三点定位原理和双脚架柔性结构原理设计了相机支撑结构，以相机安装点RMS值最小为目标，以基频约束条件，建立了相机支撑结构随机响应优化模型，对支撑结构直梁柔性环节位置进行了尺寸优化设计，利用有限元软件对其进行了工程分析。对满足设计要求的相机支撑结构进行了随机振动试验，结果表明所设计的支撑结构满足相机支撑结构设计指标。

1 随机振动响应的数学模型

1.1 随机响应模型

根据弹性力学有限元法可知，任何系统的运动都可表示为内力、外力和惯性力的平衡方程组，用式(1)表示

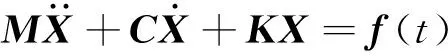
(1)

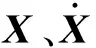
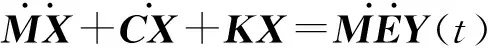
(2)

式中：E为加速度指示向量。

首先求解系统的固有模态，令C=0，f(t)=0，可得系统的自由运动方程为

(3)

其对应的特征方程为

K-w2M=0

(4)

(5)

式中：ξi为系统第i阶模态的阻尼比；Υi为第i阶振型参与系数，Υi=φTME

(6)

X(t)和ui的关系为

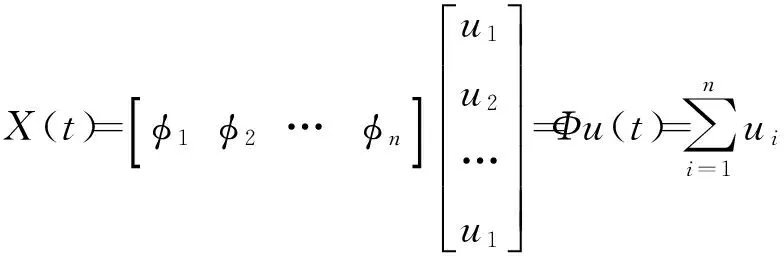
(7)

式(5)在时域内的解为

(8)

式中：hi(τ)为系统的第i阶脉冲响应函数。

将式(8)代入式(7)可得

(9)

则的自相关函数矩阵为

(10)

根据维纳-辛钦(Winner-Khinchin)关系[5-6]，输出功率谱密度是输出自相关函数的傅里叶变换，交换积分次序，引入变量代换θ=t+τ1-τ2，得输出功率谱密度函数为

(11)

(12)

工程上一般使用简化近似法，忽略掉式(12)中的交叉项，响应功率谱密度简化为

(13)

均方根响应为

(14)

1.2 灵敏度分析

模态分析用于确定设计中结构的振动特性，即系统结构的固有频率和振型，是考察动态刚度的重要指标，结构低阶模态也是修改结构的重要依据。对结构模态灵敏度进行如下分析。

设λi和{φi}是第i个孤立特征值和对应的模态向量，则他们满足特征方程

([K]-λi[M]){φi}=0

(15)

令λi,j和{φi,j}为λi和{φi}对设计变量tj(j=1,2,…,L)的导数，[K,j]和[M,j]为[K]和[M]对tj的导数矩阵，则特征值的灵敏度λi,j和模态向量的灵敏度{φi,j}为

λi,j={φi}T([K,j]-λi[M,j]){φi}

(16)

(17)

而本文有限元尺寸优化分析的单元采用厚度为t的壳单元，因此给出了壳单元的刚度矩阵[K]e的导数矩阵和质量矩阵[M]e的导数矩阵。

(18)

(19)

对式(14)求导，即可得到随机加速度响应的灵敏度[7]。

本文采用MSC.Patran&Nastran2010来进行随机振动响应分析。在MSC.NASTRAN中，它将随机响应分析当作频率响应分析的后处理来进行[8]，并据此获得随机载荷作用下的加速度响应功率谱密度曲线与随机振动加速度响应均方根值。

2 空间相机支撑结构设计分析

相机支撑结构能很大程度上影响相机的光学性能，支撑结构应尽可能少地引入不可预测的变化，对于环境变化尤其是振动不能过于敏感，并且相机结构相对于卫星整体坐标系要能够实现精确定位[9-10]。另外，相机支撑结构还要满足长期稳定性要求。

本文利用三点定位原理[11]和双脚架柔性结构原理[12]设计了相机支撑结构，每个双脚架由两根成一定角度的支腿组成，可实现类似V型块的2个自由度约束，支撑结构中柔性装置位于双脚架结构的两个支腿上，三个双脚架以圆周形式均布在相机底面，相机通过三个双脚架组件固定到卫星本体上，从而实现相机的6自由度约束，同时，双脚架的每一个柔性装置等效于一个双臂铰链或十字型柔性装置，一定程度上避免外力耦合到相机结构上。

2.1 尺寸优化数学模型

建立以相机支撑结构基频为约束条件，相机安装点的加速度均方响应RMS值最小为优化目标的尺寸优化模型。本文的设计变量用式(20)表示，为兼顾加工工艺，优化步长取1，根据支撑结构上下安装设计要求，柔性环节距离支撑结构安装面距离取值区间为[10,105]。

T′=(t1,t2,…,te,…,tn)T

(20)

式中：te表示柔性环节距离支撑结构安装面距离。

某卫星要求相机支撑结构基频f1不小于250 Hz，本文取基频300 Hz作为优化的约束条件。相机支撑结构优化目标函数为相机安装点随机振动加速度响应均方根值RMS，用式(14)表示。

本文直梁柔性环节位置尺寸优化的数学模型

(21)

式中：te表示柔性环节距离支撑结构安装面距离；f1表示结构基频。

2.2 柔性环节位置尺寸优化

根据卫星总体设计要求，相机支撑结构高118 mm，材料选用密度小、强度高、弹性模量为10 900 kg/mm2的金属材料TC4。某卫星随机振动强迫加速度功率谱(PSD)条件如表1所示，其RMS值为10.16 grms。本文中相机支撑结构分析结构阻尼系数暂取整星结构阻尼为0.02，选择相机安装点的Z向加速度响应均方值为目标，采用OptiStruct 软件对支撑结柔性环节位置进行优化，其有限元模型如图1所示。

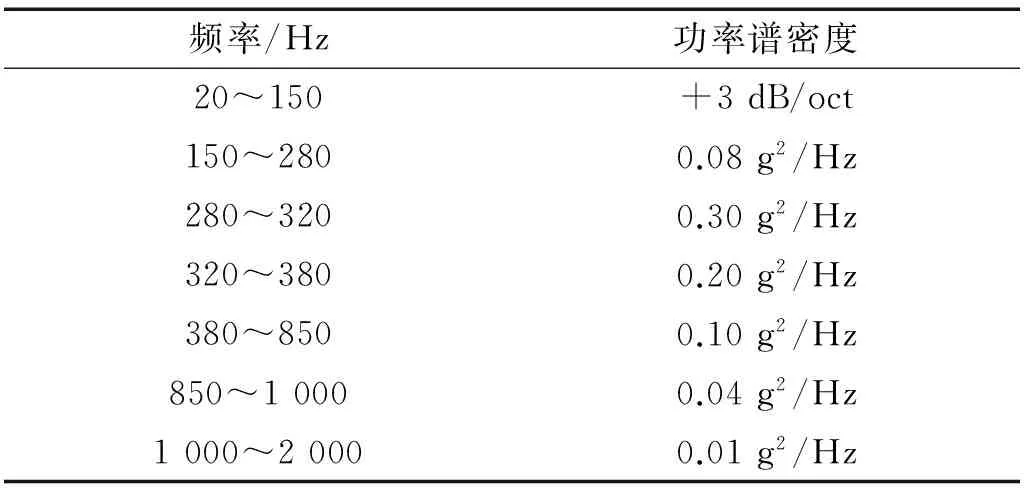
表1 激励加速度功率谱(PSD)

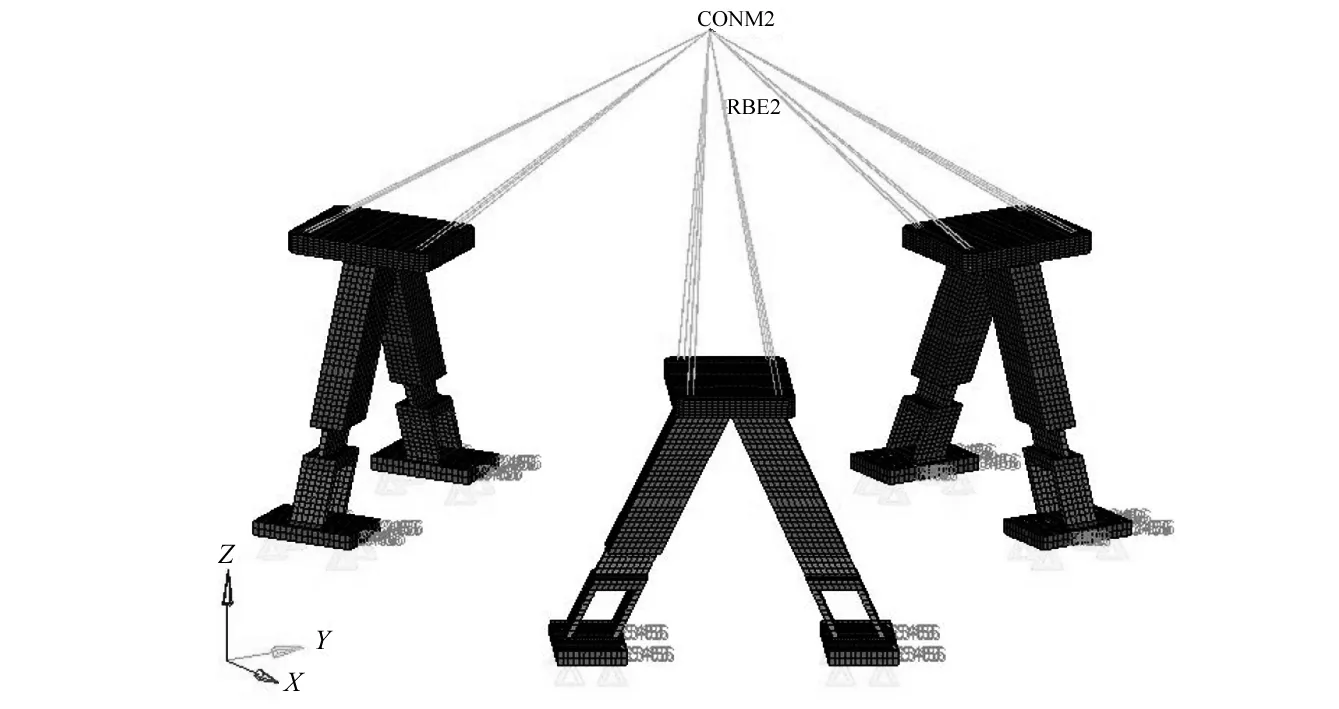
图1 支撑结构有限元模型Fig.1 The finite element model of the support structure

支撑结构迭代优化过程收敛曲线如图2所示，直梁柔性环节位置距离相机安装面98 mm时，响应最小，为14.6 grms，优化处理后的模型如图3所示。

图2 迭代收敛曲线Fig.2 Iterative convergence curve

图3 优化后的模型Fig.3 The new model after optimizing

2.3 优化后有限元分析

利用MSC. Patran & Software2010对优化处理后的

相机支撑结构建立有限元模型，并进行模态和随机振动分析, 采样点位置如图4所示，表2列出了相机支撑结构的前3阶固有频率，位于支撑结构上端与相机MPC连接采样点的加速度功率谱(PSD)响应曲线如图5所示，表3列出了相机支撑结构x,y,z三个方向的采样位置响应随机振动响应最大值节点分析结果。

表2 相机支撑结构前3阶固有频率

图4 采样点位置Fig.4 Sampling point

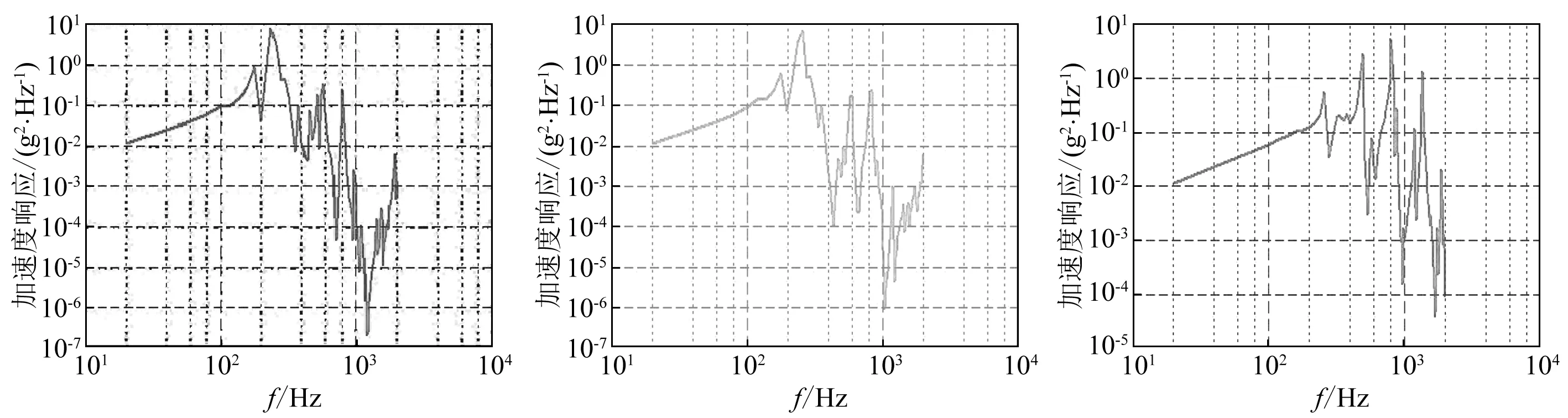
(a)x向 (b)y向 (c)z向图5 加速度功率谱(PSD)响应曲线Fig.5 Acceleration power spectrum response curve(PSD)

阶次频率/Hz振型x/grmsy/grmsz/grms15.615.319.3

3 试验验证

为了验证随机振动响应下空间相机支撑结构设计的合理性和有限元数值分析结果的准确性，利用型号为MPA3436/H1859A的振动试验台，按表1中条件在室温下对其进行振动试验。试验现场如图6所示，图7为相机支撑结构x,y,z三个方向随机振动响应的试验曲线，表4为随机振动响应试验结果与分析数据的对比。

图6 振动试验现场Fig.6 Placement of random vibration test

(a)x向

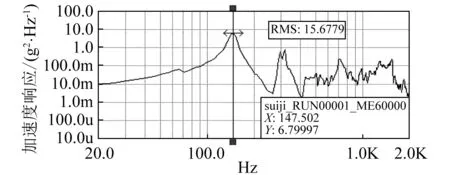
(b)y向

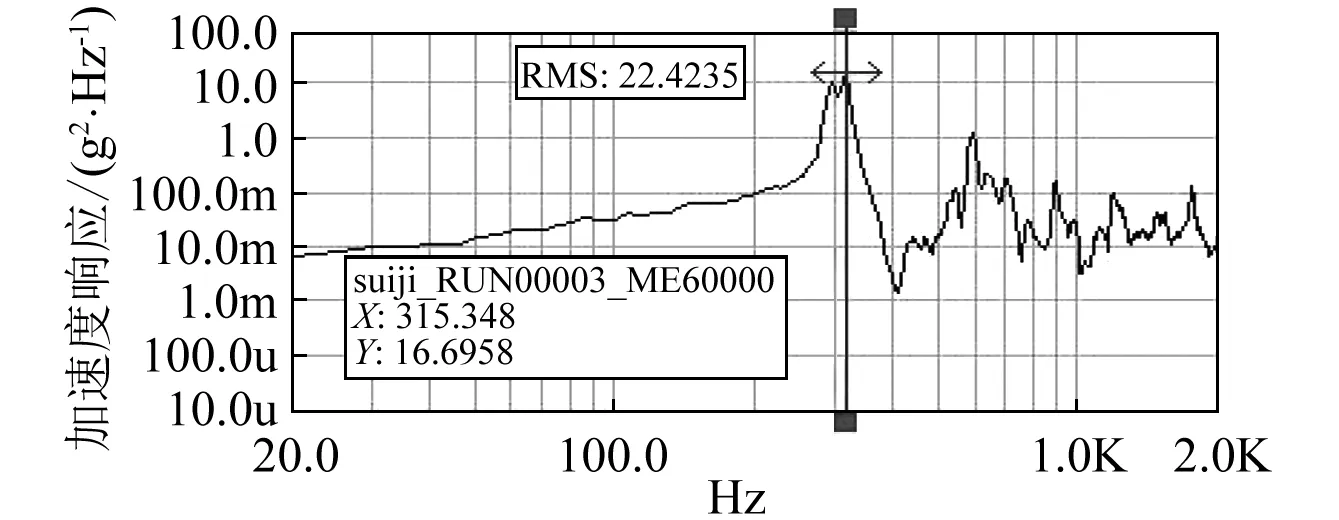
(c)z向图7 采样点PSD响应曲线Fig.7 The PSD response curve to sampling points

根据表4，本文设计的相机支撑结构随机振动响应有限元分析数据与振动试验数据误差均在10%以内，其中x向相对误差为8.2%，对应采样点随机振动响RMS值为19.4 grms，本文有限元分析时结构阻尼取整星结构阻尼0.02，可通过修正阻尼系数来优化有限元分析结果。该结果验证了本文中有限元模型的正确性和优化方法的可行性。

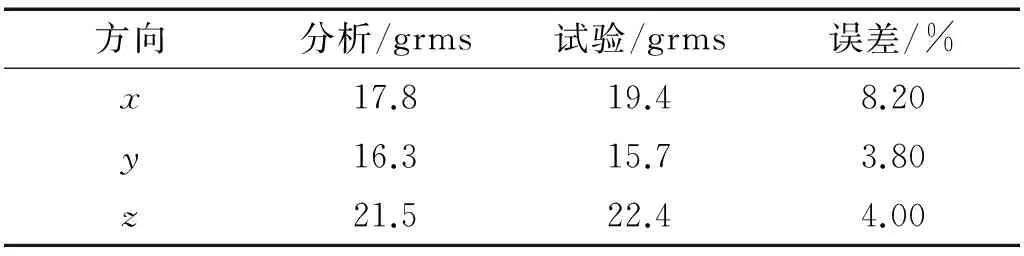
表4 试验与分析数据对比

4 结 论

本文通过建立随机振动响应分析的数学模型，推导了随机振动均方根响应近似表达式，在此基础上，利用三点定位原理和双脚架柔性结构原理对空间相机支撑结构进行了详细设计，以相机安装点随机加速度相应RMS值最小为目标对柔性环节位置进行了优化设计，对优化后的支撑结构进行了工程分析和随机振动试验。柔性环节距离支撑结构安装面98 mm时相机安装点最大响应19.6 grms。目前，该空间相机支撑结构已应用于工程项目中。

[1] 毛国斌.某航天器姿态控制机组随机振动响应分析[J].上海航天，2007(3):54-57.

MAO Guobin. Random vibration response prediction of some spacecraft attitude-control thruster set[J]. Aerospace Shanghai，2007(3)：54-57.

[2] 张军，谌勇，张志谊，等.卫星随机试验的振动响应分析[J].机械强度，2006,28(1):16-19.

ZHANG Jun, CHEN Yong, ZHANG Zhiyi, et al. Research on the random vibration test of the satellite[J]. Journal of Mechanical Strength, 2006,28(1):16-19.

[3] 杨新峰，赵志明，邓卫华，等.小卫星随机振动特性分析与试验验证方法探讨[J].航天器环境工程，2014,31(4)：357-362.

YANG Xinfeng, ZHAO Zhiming, DENG Weihua, et al. Random vibrations of small satellites and the testing method[J]. Spacecraft Environment Engineering, 2014,31(4)：357-362.

[4] 张玉梅,韩增尧,邹元杰.航天器随机振动设计载荷有限频段法研究[J].航天器工程，2013,22(1):49-52.

ZHANG Yumei, HAN Zengyao, ZUO Yuanjie. Research on limited frequency bandwidth method of spacecraft design load for random vibration[J]. Spacecraft Engineering, 2013,22(1):49-52.

[5] 陈志敏，朱海潮，匡贡献.基于二阶循环统计量的近场声全息试验研究[J].振动与冲击，2011,30(9)：202-206.

CHEN Zhimin, ZHU Haichao, KUANG Gongxian. Experimental study on near-field acoustic holography based on the second-order cyclic statistics[J]. Journal of Vibration and Shock, 2011,30(9):202-206.

[6] 盛骤,谢式千,潘承毅.概率论与数理统计[M]. 3版. 北京:高等教育出版社,2001.

[7] 鲁亚飞，范大鹏，范世珣，等．快速反射镜两轴柔性支承设计[J]．光学精密工程，2010，18 ( 12 ) :2574-2582．LU Yafei，FAN Dapeng，FAN Shixun，et al．Design of two axis elastic support for fast steering mirror[J]. Opt Precision Eng, 2010，18(12): 2574-2582.

[8] 田利思，李相辉，马越峰，等. MSC Nastran 动力学分析指南[M]. 北京：中国水利水电出版社，2012.

[9] 王忠素，翟岩，梅贵，等.空间光学遥感器反射镜柔性支撑的设计[J].光学精密工程，2010，18(8)：1833-1840.

WANG Zhongsu, ZHAI Yan, MEI Gui, et al. Design of flexible support structure of reflector in space remote sensor[J]. Opt Precision Eng , 2010, 18( 8) : 1833-1840.

[10] 闫勇, 贾继强, 金光. 新型轻质大口径空间反射镜支撑设计[J].光学精密工程, 2008, 16(8): 1533-1539.

YAN Yong, JIA Jiqiang, JIN Guang. Design of new type space borne light weighted primary mirror support[J]. Opt Precision Eng, 2008, 16( 8): 1533-1539.

[11] 王辉.极紫外光刻系统物镜光学元件的支撑与分析[J].中国光学与应用光学，2010，3(6)：598-604.

WANG Hui. Objective optical mounts and analysis for EUVL[J]. Chinese Journal of Optics and Applied Optics, 2010，3(6)：598-604.

[12] 崔永鹏，何欣.遥感仪器光学系统用非球面反射镜的支撑结构设计[J].红外, 2013, 34(10): 16-19.

CUI Yongpeng, HE xin. Design of support for aspheric mirror used in remote sensor[J]. Infrared, 2013, 34(10): 16-19.

Design and test of a space camera support structure under random vibration excitation

LI Lin1,2, WANG Dong1,3, KONG Lin1,3, TAN Luyang1,2, YANG Hongbo1

(1.Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Science, Changchun 130033, China;2.University of Chinese Academy of Science, Beijing 100049, China;3.Chang Guang Satellite Technology LTD., Changchun 130033, China)

In order to solve the random vibration acceleration response of a high resolution space camera, the main support structure of the space camera was optimally designed. A mathematical model was established based on random vibration responses, and the random vibration root-mean-square response expression was deduced. Then, the camera supporting structure was designed by virtue of the principle of three point location and the idea of bipod flexible structure. Taking the RMS of acceleration response as an objective function and the natural frequency as a constraint, the sizes of the support structure were optimized. The position of the flexible link was also optimized. Using the MSC.Patran & Nastran finite element software to analyse the support structure, it is shown that the RMS of random response at the camera installation point is less than 19.6 grms. Finally, the camera support structure was tested under random vibration excitation. The results show that the maximum relative error of the random vibration response between the analysis result and test result is 8.2%.The performance parameters of the main support structure can meet the requirements of space camera, and the feasibility of the optimization method was verified.

space camera; supporting structure; random vibration response; topology optimization; power spectral density

国家863计划项目(2012AA121502)

2015-09-07 修改稿收到日期： 2016-01-14

李林 男，博士生，1989年8月生

王栋 男，博士，副研究员，1982年2月生

V423.4

A

10.13465/j.cnki.jvs.2017.10.037