初中数学概念要注重“三化”

单芳兰

摘 要：概念教学是初中数学教学的重点内容。在“学为中心”的课堂教学理念下，初中数学概念教学要走出“呈现概念——讲解概念——练习概念”的单一化模式。要基于生活现实情境，让概念引入动态化；借助数形结合，让概念形成过程化；设计针对性练习，让概念理解深刻化，以此来提升学生学习数学概念的效果。

关键词：数学概念；动态化；生活化；过程化

【中图分类号】G 【文献标识码】B 【文章编号】1008-1216（2017）04B-0080-02

数学概念教学是初中数学教学的重点内容之一，对于初中生而言，其在对数学概念进行理解时，如果缺乏深刻性理解，那么也就无法实现高效化的数学学习。数学概念具有自身的特点，其中就包括抽象性强的特征，而初中生还处于成长阶段，其思维主要体现为形象思维。由此可见，在数学概念学习中，学生的思维与教学内容存在明显的不匹配性。当前，很多教师在教数学概念时，大都采取“呈现概念——讲解概念——练习概念”的模式。尽管该教学模式也具有一定的可行性，但是该模式，不利于初中生主动学习数学概念。“学为中心”的课堂教学理念，强调学生学习的自主性。基于此，在进行初中数学概念的教学活动中，教师需要结合初中生特有的思维特点，在数学概念的引入阶段、形成阶段及深化阶段，采取化抽象为形象这个策略引导初中生进行自主学习。

一、基于生活情境——将概念学习引入动态化

在概念教学中，引入概念是首要环节。部分教师在落实该环节时，则直接以文字的形式进行展示。由于学生与数学概念之间存在一定的感知距离，若采取该方式，则对学生深入学习概念不利。事实上，在生活中，经常能找到数学概念的影子，而借助相应的生活情境，能使抽象的数学概念形象化。为此，从教师这个层面上来说，学会通过链接生活情境的方式，来引入数学概念就显得非常重要。

（一）模拟生活场景，引入数学概念

从客观层面来说，数学概念本身就源于生活，也就是说，能在生活中找到数学概念的原型。在进行初中数学概念课的教学活动中，通过创设相应的情景方式，来引入本节课需要教学的数学概念，帮助学生提升对数学概念的有效感知。

例如，笔者在给初中生引入“数轴”这一数学概念时，首先给学生呈现了这样一个生活化的场景：王华家、电影院、游乐场在同一条街上，从王华家出发向东走200米是电影院，向西走300米是游乐场。然后提问：“如果把向东走规定为正，向西走规定为负，你能用一幅简单的图表示王华家、电影院、游乐场这三者之间的位置关系吗？这样，学生就通过自己的表示方法画出王华家、电影院、游乐场之间的位置关系，在学生画示意图的基础上，我再抽象出数轴的概念来，这样引入数轴的概念，学生就很容易理解。

以上案例中，借助生活场景来引入数轴的概念，就能够让学生充分感知数学概念在生活中的广泛应用，能够对数轴这一概念的本质特点进行把握，为他们接下来探究数轴的三要素奠定了基础。

（二）迁移生活经验，引入数学概念

初中生学习数学概念，是其进行数学学习非常重要的一部分。而在学习的过程中，学生经常会带有自身的生活经验，“学为中心”的教学理念，就强调经验性教学的内容。为此，教师在引导初中生学习数学概念的过程中，要合理引入学生原有的生活经验，并在进行生活经验迁移的过程中，适当引入数学概念。

例如，笔者在给学生引入“平面直角坐标系”这一数学概念时，首先给学生呈现了电影院的位置图，然后出示一张“7排9号”的电影票，引导学生结合电影院里的位置图，说一说“7排”和“9号”表示的意思，并找到相应的位置。在学生发言的基础上，引导学生深入讨论“电影票为什么要用几排几号”来表示。学生结合自己的生活经验很快明白用“几排几号”表示位置关系的重要性。此时，笔者利用动画把电影院里的位置图抽象成平面直角坐标系的一个雏形。这样，学生在这个过程中就能够直观化地感受到“平面直角坐标系”的推导过程。

以上案例中，结合学生找电影院里的位置这一生活经验，引入“平面直角坐标系”的概念，这样自然就能激发学生学习这一数学概念的兴趣。

二、借助数形结合——让概念形成过程化

数学是研究“数”与“形”的学科，“数”与“形”这两者之间联系非常紧密。为此，在初中阶段，进行数学概念的教学时，结合数形的教学形式能有效地促进学生理解数学概念的形成过程。

（一）借助数形结合，理解数学概念的本质

在初中数学教材中，对于部分数学概念的呈现，在很多地方经常缺乏“形”这个要素，导致学生无法对数学概念的本质进行有效地掌握，在认知上只能停留在表面。为此，在实际教学过程中，对于教师而言，要善于借助数形结合这种教学方式，以此来引导学生对数学概念的本质进行理解。

例如，笔者在给学生教学《三角形的中位线》时，在引入“三角形的中位线”这一概念以后，组织学生在白纸上任意画一个三角形，这样，有的学生画出了直角三角形；有的学生画出了锐角三角形；有的学生画出了钝角三角形，然后，我让学生分别去量一量自己畫的三角形中，一条底及对应中位线的长度，学生在这个过程中发现了三角形的中位线是对应的底边长度的二分之一。最后，我组织学生以四人小组为单位进行交流讨论，他们在交流讨论的过程中，明白了这一种关系不是巧合，不管是锐角三角形、直角三角形还是钝角三角形，其边对应的中位线的长度都是这一条边长度的一半。

以上案例中，对于三角形中位线的性质，教师没有向学生事先进行讲解，而是通过让学生画三角形的中位线、量三角形中位线与对应底边的长度，使学生在数形结合的过程中，对“三角形中位线”这一概念的本质有了深刻的了解。

（二）借助数形结合，把握数学概念的核心

不管是哪一个数学概念，都存在相应的核心词，且该核心词能起到关键作用。对于学生来说，在形成数学概念的过程中，一旦能把握数学概念的核心词，就能提升概念学习的效率。为此，在具体的教学实践过程中，借助数形结合这个策略，引导学生对数学概念的核心词进行把握，促使学生能深入理解数学概念。endprint

例如，笔者在引导学生学习“绝对值”这一概念时，让他们在数轴上先去找一找3、-3、-11、11的位置，然后，根据绝对值的概念去算一算这一些数的绝对值。基于数轴上的点到原点的距离这一关键点，他们一下子就发现了3和-3、-11和11的绝对值是一样的。此时，笔者引导学生思考为什么这两组数的绝对值是一样的，学生结合数轴就很容易明白3和-3离原点的距离都是3，11和-11离原点的距离都是11，所以绝对值是相同的，所不同的是，这两组数距原点的方向是相反的，绝对值只与距离这个因素有关，而与方向无关。

以上案例中，结合数轴引导学生学习“绝对值”的概念，能够有效地让学生经历探究“绝对值”这一数学概念的核心词的过程，使学生能够在数形结合下，有效地对这一数学概念的本质内涵进行内化。

三、设计针对练习——让概念理解深刻化

在初中数学概念教学的过程中，如何有针对性地为学生设计数学练习显得尤为重要。这是由于初中生只有通过开展练习，才能够在脑海中将数学概念牢牢记住。然而，数学概念的练习并非单纯的死记硬背，必须将数学概念的本质作为基础，进而有针对性地加以设计。

（一）设计对比性练习，深化数学概念

学习数学概念的整个过程通常来说较为枯燥乏味，因而在初中生学习时，特别是他们的数学概念已经形成之后，教师应当以数学概念的本质作为基础，有针对性地为他们设计一些对比性练习，以促进他们对数学概念进行深化理解。

例如，在教学完“代数式”这一概念之后，笔者给学生设计了以下对比性练习：我先让学生写出“x和y差的平方”与“x与y的平方差”，根据对应的数量关系，学生写出了“（x-y）2”“x2-y2”这两个代数式。然后，我引导学生对这两个代数式进行深入分析，找到这两者之间存在的区别。这样，学生在这个过程中就能够充分地体验到“x和y差的平方”与“x与y的平方差”的不同，虽然从表面上看是很相似的，但是，写出来的代数式却完全不同，从而对“代数式表示的是数与字母之间的运算关系”这一本质内涵进行深入理解。

可见，在初中数学概念教学中，在练习环节为学生设计具有对比性的练习能够有效地促进学生对数学概念的深入理解，把握数学概念的本质内涵。

（二）设计变式性练习，深化数学概念

在初中数学概念课的教学过程中，教师必须积极开动脑筋为学生设计一些变式性练习，从而使他们对数学概念的理解更加深刻。因为变式练习能够有效地让学生对数学概念的本质内涵进行深入剖析。

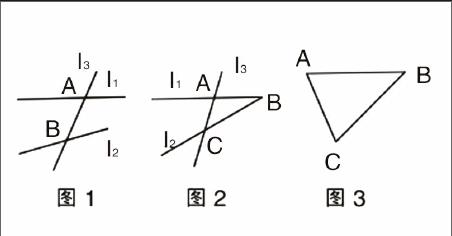
例如，在教学《同位角、内错角和同旁内角》时，新授课环节一般是通过图1中的“三线八角”引导学生认识同位角、内错角和同旁内角，图1中的“三线八角”是一种标准化的位置关系，其各个角之间的位置关系都比较明晰。如果在练习环节还是用图1中的“三线八角”，学生的数学学习就缺乏了挑战性，因此，在练习环节可以给学生出示图2和图3，在图2与图3中“三线八角”的位置关系就没有那么明晰了，因为这两个图中是对“三线八角”的变式，让学生在这两幅图中找同位角、内错角和同旁内角，就能够有效地促进他们对这些数学概念的内化吸收。

在初中数学概念教学中，有很多数学概念在练习环节都可以通过变式的形式进行练习，通过变式练习不仅能够帮助学生对数学概念进行内化，而且还能够培养他们的数学思维能力。

四、结束语

总而言之，在整个初中数学教学过程中，概念教学是不容小觑的重要组成部分。在开展这部分教学时，作为教师，我们必须要远离传统的“讲解式”，应当站在学生的角度对练习进行有针对性的设计，要通过课堂的讲授，让原本抽象的概念在学生的脑海中形成形象化的认识。唯有这样，才能确保初中生更加有效地理解和掌握數学概念。

参考文献：

[1]陈凤腾.初中数学概念教学探析[J].福建教育学院学报，2015，（11）.

[2]冯新.初中数学概念类知识建构教学设计[J].求知导刊，2016，（5）.endprint