基于《课标》理念的初中数学校本作业优化设计初探

郭丽琴

[摘 要] 数学作业是数学教学活动的重要组成部分，是巩固知识、形成技能、反馈教学效果、调整教学策略的重要手段，是课堂教学的补充与延伸. 本文根据《义务教育数学课程标准》的理念，分析了作业校本化的必要性，提出要设计再现性作业、趣味性作业、层次性作业的观点，从而促进学生的发展.

[关键词] 《课标》理念；校本作业；优化设计

问题的提出

众所周知，学生的“作业”往往被分为“课堂作业”和“课后作业”，“课后作业”一般在家中完成，因此常常称为“家庭作业”. 课后作业一直以来都是学校教育教学活动的重要组成部分，被看作是一项有价值的教育手段，是教学过程中必不可少的环节，是巩固知识、形成技能、反馈教学效果、调整教学策略的重要手段，是课堂教学的补充与延伸. 我国古代教育家孔子就提出了“温故而知新”的教育理念，说明了重复、复习知识的重要性，因此课后作业对知识的巩固有着重要的作用.

然而，传统的课后作业，除了教科书上的课后练习外，主要还是以教辅材料为主. 但教辅材料面对的是绝大多数的学校和学生，学校与学校之间、学生与学生之间均存在很大的差异. 况且，传统的数学作业形式单一，内容枯燥，缺乏吸引力；更有一些教师利用网络的优势，不分青红皂白地下载所谓的名校作业，一股脑儿抛给学生，使得学生的作业量加大，有量无质；作业没有弹性，缺少层次性，致使学生完成家庭作业的态度不够积极，甚至对家庭作业产生厌倦情绪. 有些学生马虎应付作业，有些甚至抄袭，换来一个按时交作业的假象. 如此一来，学生的作业质量无从保证，无法对所学知识进行有效巩固，还谈何教学质量呢？因此，如何设计出适合本校学生特点的新型课后作业，即校本作业，是摆在我们每位教师跟前的一大课题.

所谓校本作业，顾名思义，就是学校根据自身实际情况，自主设计的、体现自己学校特色、符合本校学生特点的作业. 近几年来，在学校领导的大力推行和支持下，笔者所在学校的校本作业设计开展得有声有色，作业全部由科任教师根据教学内容和《义务教育数学课程标准》（以下简称《课标》）要求，并结合学生实际自行编制，数学课后作业做到每一课时都有相应的一份校本作业，大大提高了课堂教学的针对性和有效性.

《课标》的基本理念

《课标》（2011版）提出：“数学课程应致力于实现义务教育阶段的培养目标：要面向全体学生，适应学生个性发展的需要，使得人人都能获得良好的数学教育，不同的人在数学上得到不同的发展. ”因此，新课程标准的实施对数学教学的各个方面都提出了新的要求，构建数学作业的新形式，是促进学生学习方式变革的一个重要方面. 這就要求广大一线教师要树立起新的数学作业设计理念，树立起正确的作业观，明确每节课课后作业的功能，精心设计面向全体、内容丰富多彩、形式新颖多样，能极大调动学生学习兴趣，引导学生关注生活，使学生在生活中应用数学知识，形成综合能力，为学生的终身发展奠定坚实的基础. 数学课后作业只有加以合理使用，才能不断提高课后作业的针对性和有效性，进而提高数学教学质量和学生的综合素质.

下面结合自己几年来的教学实践与思考，就如何基于《课标》理念和学生实际，优化校本作业设计，提高校本作业的有效性，谈谈自己的看法，以期与同行们交流、探讨.

基于《课标》理念的校本作业优

化设计

1. 根据《课标》要求，设计再现性作业，发挥作业的巩固功能

《课标》是教材编写、教学、评估和考试命题的依据，是评价管理和评价课程的基础，是我们教师教学的参考与指南. 通过对《课标》的透彻理解再去研究教材，再把书中的内容进行整合、重组、归纳、梳理，能使知识条理化、系统化. 这样设计校本作业时，就能做到心中有数、有的放矢，更好地覆盖本节课学习的主要知识点，把握好作业的广度和深度.

例如，在“用待定系数法求一次函数的解析式”中，《课标》要求：（1）能根据已知条件确定一次函数的表达式；（2）会利用待定系数法确定一次函数的解析式. 根据要求，本课时的作业设计可设计如下再现性题组.

（1）已知一次函数y=kx+2，当x =2时，y = 4，则这个函数的解析式是_______.

（2）若直线y=2x+b与y轴的交点的纵坐标是4，则该直线的解析式是______.

（3）已知一次函数y=kx+b，当x=-4时，y=9；当x=6时，y=1，求该函数的解析式.

（4）已知一次函数的图像经过点（9，0）和（24，20），求该函数的解析式.

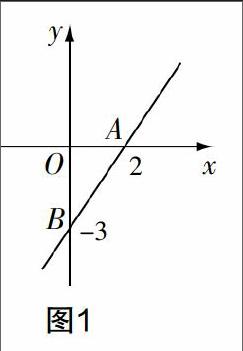
（5）如图1，一次函数的图像经过A，B两点，求这个一次函数的解析式.

（6）已知一次函数y=kx+b的图像与x轴交于点A（-6，0），与y轴交于点B，若△AOB的面积是12，求这个一次函数的解析式.

通过这一题组，把数与式、点与式、数与形结合在一起，把《课标》要求较好地落到实处，促进了学生扎实掌握双基.

2. 结合学生年龄特点，设计趣味性校本作业，激发学生的学习兴趣

传统数学作业往往形式单一，内容较枯燥，学生容易生厌. 校本作业设计时应从学生的年龄特征和生活经验出发，切入学生已有知识，设计出题型多样，方式新颖，内容具有创造性、趣味性和亲近性的数学作业，让学生感受到作业内容和形式的丰富多彩，使之情绪高昂，乐于思考，从而感受到做作业的乐趣，提高学生的作业完成质量.

例如，在“实际问题与二次函数”的作业中，可设计以下试题：

某商店经营儿童益智玩具，已知购进时的单价是20元. 调查发现：销售单价是30元时，月销售量是200件，而销售单价每上涨1元，月销售量就减少10件，当每件售价定为多少元时，才能使每月的利润最大？

这类题目富有创意，形式新颖，内容联系实际，并有一定的趣味性，能让学生切身感受到数学来源于生活，又服务于生活，能极大地激发学生的学习兴趣，唤醒学生学习的主动性.