复Finsler度量射影等价

翁 桂 英

(仰恩大学 数学系, 福建 泉州 362014)

复Finsler度量射影等价

翁 桂 英

(仰恩大学 数学系, 福建 泉州 362014)

主要研究复流形上复Finsler度量射影等价及仿射等价的若干充要条件，讨论了复Finsler流形上的测地线及2种平行移动，从而得到复Finsler度量仿射等价的另一充要条件，并将其应用于乘积复Finsler流形中.

复Finsler度量; 测地线; 射影等价; 仿射等价; 乘积复Finsler度量

Projectively equivalent complex Finsler metrics. Journal of Zhejiang University(Science Edition), 2017,44(2):154-160

流形上Finsler度量的射影等价性是Finsler几何的一个重要课题，文献[1]在实Finsler度量下研究了一般射影等价及仿射等价成立的充要条件.复Finsler度量的射影等价这一概念由YAN[2]和ALDEA等[3-6]于2012年引入并进行研究.本文将对复Finsler度量的射影等价、仿射等价性及复Finsler流形上的2种平行移动进行研究并给出其应用例子.

1 预备知识

首先,简单介绍本文所需的一些记号，更多细节参见文献[7].

定义1[7]复流形M上的连续非负函数F:T1,0M→R+若满足下列条件,则称其为复Finsler度量:

3)任意v∈T1,0M,ξ∈C,F(ξv)=|ξ|F(v).

赋有复Finsler度量的复流形称为复Finsler流形，简记为(M,F).

下文若不特别说明,复Finsler度量总表示强拟凸的.

(1)

且称D为(M,F)上的Chern-Finsler(c.n.c.)联络.

在局部坐标下,Chern-Finsler(c.n.c.)联络系数为

(2)

定理2[8]设 (M,F)为复Finsler流形, 则其为复Berwald当且仅当 (M,F) 为Kähler且为弱的复Berwald度量.

2 测地线

由文献[7],复Finsler流形上的测地线需满足:

(3)

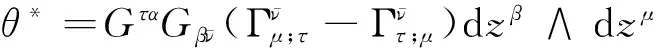
从而，测地线σ=σ(s)需满足:

(4)

证明 充分性. 在局部坐标系下, 有

因此，

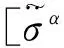
必要性显然.

3 射影等价及仿射等价

因此，

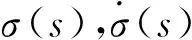
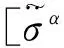
由σ(s)的正则性, 得

等式两边积分，有

最终得到

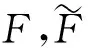
必要性显然.

(5)

注4 若一阶齐次函数P1(z,υ)满足式(5),S为(0,1)阶齐次,则P2=P1+S也为一阶齐次,且P2亦满足式(5);反之,若一阶齐次函数P1(z,υ),P2(z,υ)满足式(5),则S=P2-P1为(0,1)阶齐次.故满足式(5)的一阶齐次解相差一个(0,1)阶齐次函数.

(6)

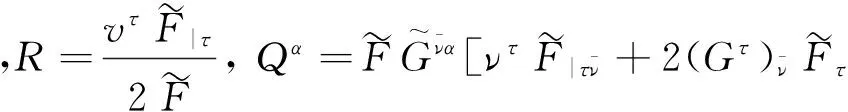
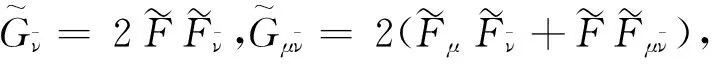
所以，

(7)

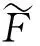
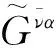
(8)

(9)

将式(9)代入式(7),可得

(10)

因此，

(11)

而且，

代入式(11),定理7得证.

反复利用式(6)可得：

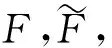
证明 1)⟹2)

(12)

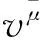
因此，有

2)⟹3)

3)⟹1)

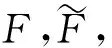
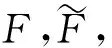
(13)

由Gτ为(2,0)齐次,可知

必要性显然.

结合定理10和定理11，可以得到以下结论：

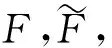
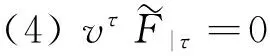
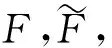
4 平行移动

如不特别说明,下面复Finsler流形均指弱Kähler,其测地线σ=σ(s)满足二阶微分方程

定义5 复Finsler流形(M,F)上,σ=σ(s)为光滑正则曲线,U=Uα(s)∂α|σ(s)为沿着σ定义的向量场,则U(s)沿着σ的线性共变导数:

(14)

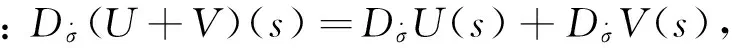
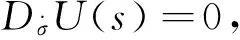
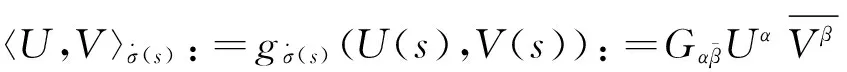
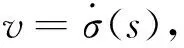
注意到F为Kähler,则

定义7 弱Kähler-Finsler流形(M,F)上,设σ=σ(s)为光滑正则曲线,U=Uα(s)∂α|σ(s)是沿着σ定义的向量场,那么U(s)沿着σ的共变导数:

(15)

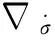
证明 由于

因此，

注意到

经化简, 可得

又因为

则

即F(σ(s),U(s))为常数.

例1 设二元函数f:R2→R+满足:对任意的λ>0,f(λs,λt)=λf(s,t),且对于任意的 (s,t)≠(0,0)，f(s,t)>0.

又(Mi,αi),i=1,2为Hermitian度量,M=M1×M2,M1为n维,M2为m维复流形. 可以构造新的度量

fs>0,ft>0,fs+sfss>0,ft+tftt>0

及

fsft-ffst>0.

Ga(z,v)=Ga(z1,v1)，Gα(z,v)=Gα(z2,v2),

[1]CHENSS,SHENZM. Riemann-Finsler Geometry[M]. Singapore: World Scientific,2005:1-85.

[2] YAN R M. Affinely equivalent Kähler-Finsler metrics on a complex manifold[J]. Science in China： Mathematics,2012,55(4):731-738.

[3] ALDEA N, MUNTEANU G. On projective complex Randers changes[J]. Bulletin of the Transilvain University of Brasov,2012,54(4):1-10.

[4] ALDEA N, MUNTEANU G. On projective invariants of the complex Finsler spaces[J]. Differential Geometry and Its Applications,2012,30(6):562-575.

[5] ALDEA N, MUNTEANU G. Projectively related complex Finsler metrics[J]. Real World Applications,2012,13(5):2178-2187.

[6] ALDEA N, MUNTEANU G. The main invariants of a complex Finsler space[J]. Acta Mathematica Sciential,2014,34(4):995-1011.

[7] ABATE M, PATRIZIO G. Finsler Metrics-a Global Approach with Applications to Geometric Function Theory[M]. Berlin: Springer-Verlag,1994:1-101.

[8] ZHONG C P. On real and complex Berwald connections associated to strongly convex weakly Kähler Finsler metric[J]. Differential Geometry and Its Applications,2011,29:388-408.

[9] ZHONG C P. On unitary invariant strongly pseudoconvex complex Finsler metrics[J]. Differential Geometry and Its Applications,2015,40:159-186.

[10] ALDEA N, MUNTEANU G. On complex Landsberg and Berwald spaces[J]. Journal of Geometry and Physics,2012,62(2):368-380.

[11] 肖金秀,严荣沐.复Finsler流形上的两个问题[J].厦门大学学报:自然科学版,2006,45(5):614-616. XIAO J X, YAN R M. Two topics in complex Finsler geometry[J]. Journal of Xiamen University: Natural Science,2006,45(5):614-616.

[12] WU Z C, ZHONG C P. Some results on product complex Finsler manifolds[J]. Acta Mathematica Scientia,2011,31B(4):1541-1552.

WENG Guiying

(DepartmentofMathematics,YangenUniversity,Quanzhou362014,FujianProvince,China)

complex Finsler metrics; geodesics;projectively equivalent; affinely equivalent; product complex Finsler manifold

2016-01-28.

翁桂英(1983-),ORCID:http://orcid.org/0000-0002-3469-1466,女,硕士,讲师,主要从事多复变数和复Finsler几何研究,E-mail: yeuwgy@163.com.

10.3785/j.issn.1008-9497.2017.02.006

O 186.1

A

1008-9497(2017)02-154-07