三维迷宫的设计与建模

王 康，吴文明，刘利刚

(中国科学技术大学 数学科学学院， 安徽 合肥 230026)

三维迷宫的设计与建模

王 康，吴文明，刘利刚*

(中国科学技术大学 数学科学学院， 安徽 合肥 230026)

三维迷宫在难度和趣味性上达到了一个更高的水平.通过改进二维迷宫的生成算法，提出了循环迷宫的概念和迷宫复杂度公式.进而，提出一种基于四边形网格曲面的三维迷宫设计算法.该算法分3个步骤：首先，将给定的三维曲面四边形网格化；再确定迷宫的起点和终点，采用基于生成树的二维迷宫生成算法，在网格表面生成迷宫路径；最后，将迷宫实体化为三维结构，并与原始三维模型做布尔运算，得到三维迷宫.通过3D打印机制造出个性化的三维迷宫玩具，大大增强了迷宫的趣味性，改善了用户体验.

三维迷宫；建模；生成树；复杂度；三维打印

0 引 言

迷宫是一种古老的意象，在古代是完整的象征[1].迷宫建筑因其神秘性而令无数爱好者着迷；迷宫游戏亦因其趣味性强而广受大众喜爱；作为一种儿童学前教育的益智玩具，迷宫玩具备受家长青睐.迷宫的相关研究与设计已取得了一些成果[2-5]，该领域具有广阔的市场前景.

PHILLIPS[6]研究了罗马马赛克式迷宫拓扑，提出一套用于破损迷宫重建和保存的迷宫重建理论.MCCLENDON[7]提出了一种计算曲线迷宫复杂度的方法：在迷宫的路径曲线上定义连续函数，考虑路径长度、极值点等因素对复杂度的影响，利用连续化方法提出了曲线迷宫复杂度的计算公式.在迷宫设计方面，XU等[8]提出了一种带有漩涡结构的复杂迷宫生成算法，后又提出基于图像的迷宫算法[9]，即通过扩展传统的迷宫生成算法建立适应图像风格的迷宫.

将迷宫由二维空间推广到三维空间，增加了迷宫的难度，同时也令其更具挑战性、趣味性与可玩性，对玩家空间能力的培养大有裨益.虽然出现过一些三维迷宫的设计方案，但难以实现批量生产，也尚未出现相关的设计软件.一方面，设计者要在三维空间中构思迷宫的结构，设计难度远远高于二维迷宫；另一方面，三维的设计也加大了迷宫游戏的难度，复杂的三维结构超出玩家的能力范围.

二维迷宫设计简单，而趣味性低；三维迷宫设计复杂，但操作性强.自然的想法是结合二维迷宫与三维结构得到三维迷宫.如图1所示，通过将二维迷宫(a)嵌入到三维模型(b)表面，得到一个实体的三维迷宫(c).这样的三维迷宫设计虽然简单，但具有很高的操作性和趣味性，主要需考虑以下问题：(1)二维迷宫的约束条件，即二维迷宫满足怎样的条件才能设计成三维迷宫；(2)二维迷宫的生成算法，即如何在一般曲面上生成二维迷宫；(3)三维迷宫的生成算法，即如何将二维迷宫与三维模型合成得到三维迷宫.

图1 三维迷宫的设计思路Fig.1 The design idea of 3D maze

本文提出一种三维迷宫设计与建模方法.结合二维迷宫生成和3D建模技术，将二维迷宫嵌入三维模型表面，得到三维迷宫.三维迷宫的设计有更多约束条件，如循环迷宫；出于用户交互的需求，应该为用户提供迷宫路径可控的生成算法，即定制迷宫；考虑生成迷宫的有效性，需要量化迷宫的复杂度，等等.

1 二维迷宫的设计

1.1 迷宫的表示及约束

如图2所示，用二维数组表示二维迷宫.二维数组中的元素为0或1，0表示路径，1表示墙壁.从入口到出口之间的最短路径称为迷宫的主路径.二维迷宫需要满足以下约束条件才能设计成三维迷宫：

图2 用二维数组表示迷宫Fig.2 A maze represented by 2D array

(1)二维迷宫有且仅有一条主路径；

(2)路径之间必须有墙壁阻隔；

(3)路径中任意2个顶点之间连通；

(4)路径之间不能形成回路.

如图3所示，(a)中2条纵向路径并列在一起，不满足路径约束条件(2)；(b)中路径之间形成回路，不满足路径约束条件(4).

图3 无法设计为三维迷宫的二维迷宫Fig.3 The 2D maze which can’t be designed as 3D maze

1.2 二维迷宫的生成

二维迷宫的生成可以通过生成树算法实现.从图论的观点看，迷宫可作某个图的生成树，反之，图的生成树也可表示为一个迷宫，如图4所示.袁开等[10]基于最小生成树的Kruskal算法，用图的连通子图生成迷宫.田翠花等[11]采用图的深度优先遍历生成规则的随机迷宫.这些算法大同小异，主要步骤如下：

(1)初始化二维数组maze[m][n]；

(2)将二维数组maze[m][n]转化成图；

(3)基于某种生成树算法生成迷宫；

(4)导出随机迷宫.但存在以下问题：(1)算法对图进行盲目搜索，生成迷宫的路径是完全随机的.(2)算法同时生成迷宫的主路径和支路，不能定制迷宫.(3)生成的迷宫路径局限在矩形区域，两侧不连通，迷宫是不可循环的.

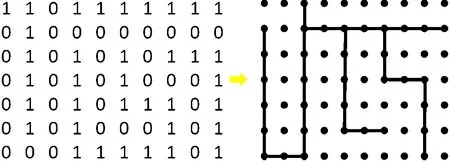
图4 迷宫与生成树等价Fig.4 A maze is equivalent to a spanning tree

笔者希望系统既能生成随机迷宫，也能定制迷宫，或者定制和随机2种形式相互混合.由于传统算法不能满足此要求，于是提出了一种新的迷宫算法，将主路径和支路的生成过程分为2个独立的阶段.

第1步 生成由指定起点到指定终点的迷宫主路径.这里提出2种生成迷宫主路径的方式：第1种通过用户交互给出主路径，此方式简单直接，亦能满足用户定制的需求.第2种基于生成树算法生成主路径，此方式能产生随机主路径.借鉴深度优先遍历算法[12]，用“穷举求解”的思路：由指定起点开始随机搜索，如果走得通，则继续搜索；否则沿原路后退一步或者多步，重新选择其他路径，至找到指定终点为止.

如果当前位置某个方向上的点及其四周的点都未被访问过，说明该方向走得通.如图5所示，黄色的点为当前位置，红色箭头表示选择右侧为考察方向.为保证生成的迷宫是规则整齐的，在实际操作中均以2步为一个操作单位.于是考察红色标记的位置，若四周(圆圈标记)的位置都未被访问过，则表示该方向走得通.

图5 方向选择Fig.5 The choice of the direction

当所有方向都走不通时，就从路径中删除该位置并后退到前一位置，重新选择路径方向.如图6所示，(a)图中当前位置(黄色标记)的四周都走不通，此时后退到上一位置，(b)图中当前位置，然后再由此位置开始，选择其他路径重新搜索，至找到指定终点为止.

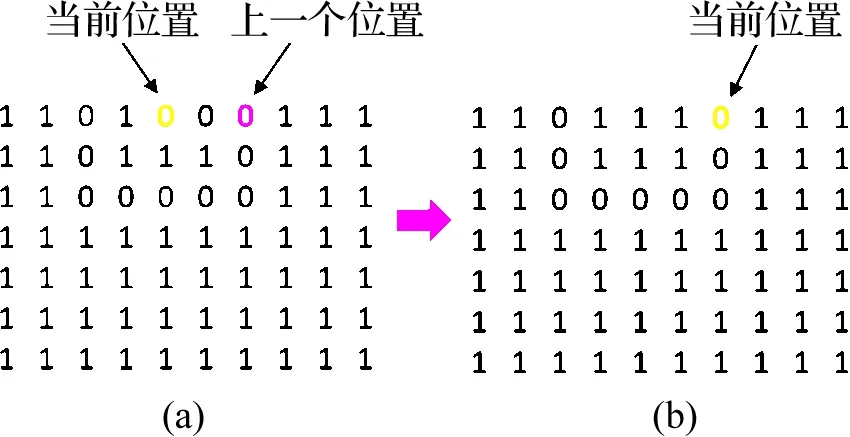
图6 回溯Fig.6 Backtrack

第2步 基于迷宫的主路径生成迷宫的支路.算法流程是依次考察主路径上的每个点，由该点开始随机搜索生成支路，其搜索不同于主路径，当四周都走不通时直接不再回溯停止搜索，继续考察下一个点，如图7所示：迷宫的主路径在图中用红色标记，沿着主路径逐点生成迷宫的支路.在实际操作中，每次间隔1个点生成迷宫的支路，这样可保证生成的迷宫路径规整.当前考察位置用黄色标记，由此位置开始随机搜索，当四周都走不通时停止搜索.这样搜索过的路径就构成一条支路，在图中用绿色标记.接着间隔一个位置继续考察下一个.依此类推，可以在生成的支路上继续生成支路，进一步完善迷宫至不能再生成支路为止.

图7 支路的生成Fig.7 The generation of the branch

1.3 循环迷宫

循环迷宫指没有边界的迷宫.将平面迷宫映射到三维曲面时，平面迷宫因三维曲面结构而发生拓扑的局部改变，使得迷宫路径可循环.循环迷宫可实现边界间“无缝”拼接.图8为非循环与循环迷宫图.

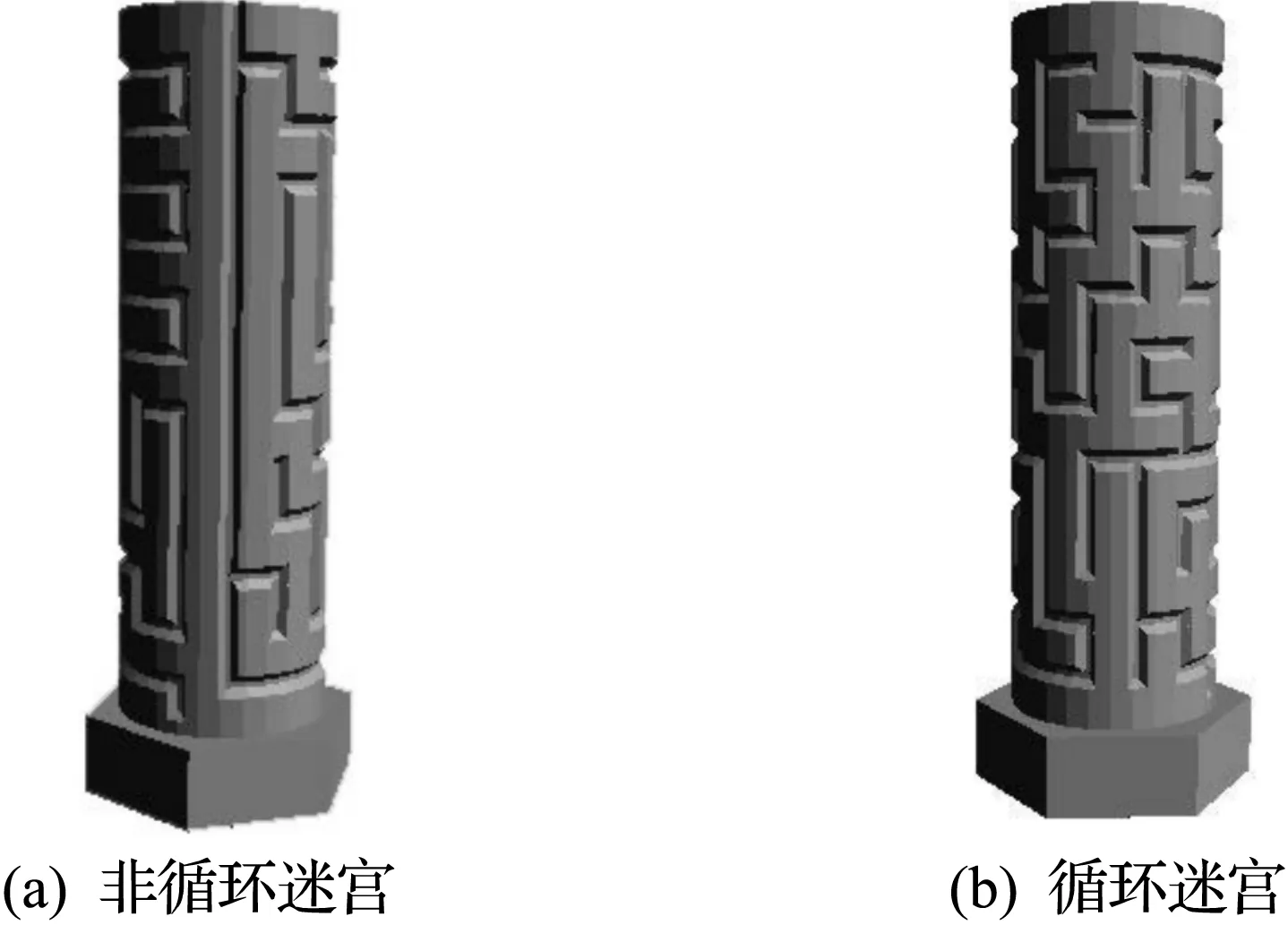
图8 非循环迷宫与循环迷宫Fig.8 Non-loop maze and loop maze

本文方法可以实现循环迷宫.如图9所示，P在左侧边界上(黄色标记)，与P相邻的点为

{PU，PD，PR},

P的左侧没有点，因此，由P无法直接访问迷宫的右侧.解决办法是在迷宫的边界处重新定义边界的拓扑.重新定义P的相邻点为

{PU，PD，PR，PL},

其中,PL是迷宫的左侧边界点.这样，在P处，就可以自由访问4个方向的点.对二维迷宫的所有边界都重新定义类似拓扑，直接将这种拓扑关系应用于迷宫的生成，则可设计出循环迷宫.

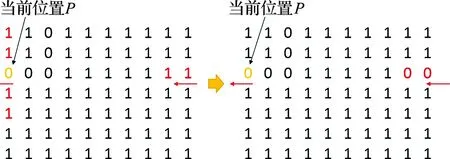
图9 循环迷宫的实现Fig.9 The implement of the loop maze

1.4 迷宫的复杂度

保证迷宫的有效性是检验迷宫设计质量的标准之一，控制复杂度是保证迷宫设计有效性的良好方法.因此，有必要引入迷宫的复杂度来指导迷宫设计.MCCLENDON[7]提出了一种计算迷宫复杂度的方法，但所讨论的迷宫是一类曲线迷宫，计算比较复杂.考虑到矩形迷宫自身离散的特点，借鉴MCCLENDON的方法，本文提出一种计算矩形迷宫复杂度的离散化方法.

当迷宫中没有支路时，则认为迷宫复杂度为0.一般来说，支路越多，支路的深度越深，迷宫就越复杂.引起支路路径方向改变的点称为支路的拐点，拐点的数量在一定程度上反映了迷宫的复杂程度.综上所述，支路的数目、长度，支路上的拐点数都是影响迷宫复杂度的因素，如图10所示.

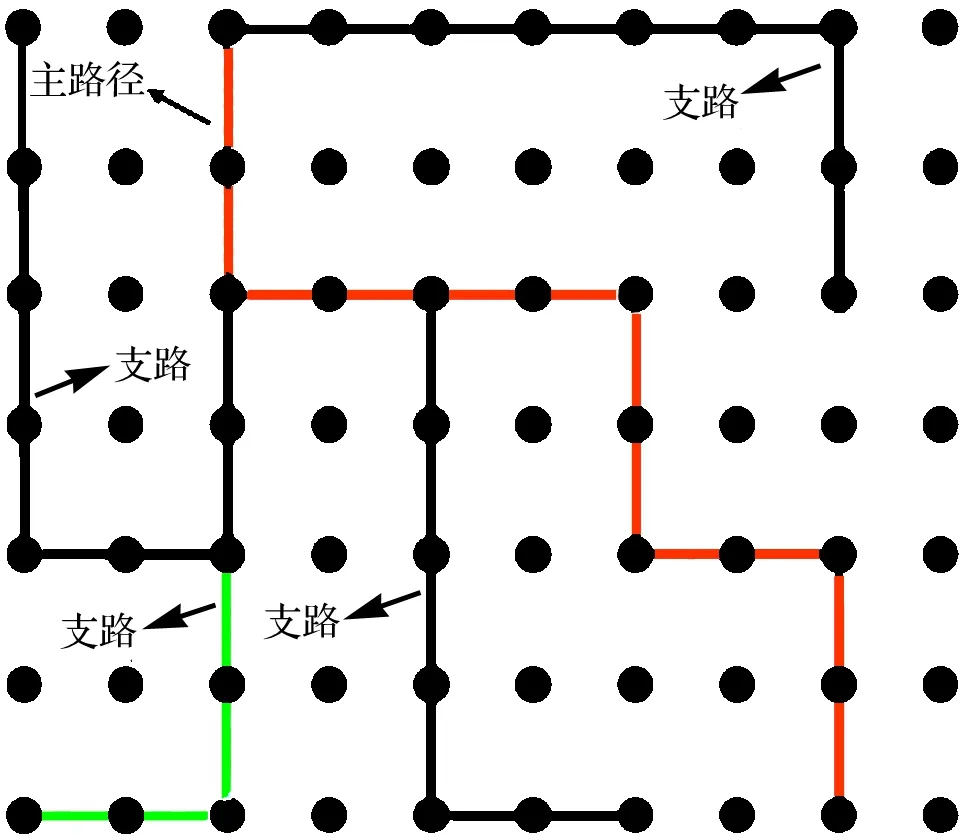
图10 影响迷宫复杂度的因素Fig.10 The influence factors of the maze complexity

设B是基于迷宫主路径生成的某条支路，称为一阶支路，在一阶支路上可以生成高阶支路.设B上的支路数为n.设Li是i阶支路的长度，

{Ci,1,Ci,2,Ci,3,…,Ci,j}

表示i阶支路的拐点集合，其中i=1,2,…，n.显然，随着支路阶数的增加，迷宫的复杂度也增大.根据用户习惯，定义迷宫支路B的复杂度为

对于给定的迷宫，特别是存在高阶支路的迷宫，支路的划分不唯一.例如图10中的支路存在2种划分，见图11.于是定义：

Branchmax(B)=Max{Branch(B)|B的所有划分},

Branchmin(B)=Min{Branch(B)|B的所有划分},

平均复杂度Branchave(B)能更好地反映迷宫支路的复杂情况.简单计算图11中支路的3种复杂度.(a)图对应的是最大复杂度：

(b)图对应的是最小复杂度：

于是平均复杂度为

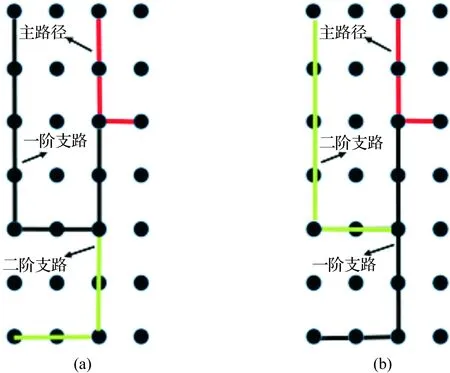
图11 支路的不同划分Fig.11 Different division of the branch

设{B1,B2,B3,…，Bn}表示迷宫主路径上的n条一阶支路，迷宫的复杂度定义为所有支路的复杂度之和.因此，迷宫的复杂度为

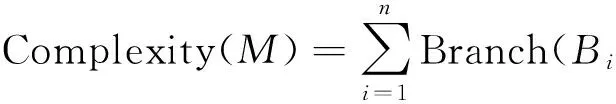
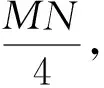
2 三维迷宫的设计

2.1 算法概述

三维模型最常见的表示方式是网格，网格所表达的三维模型具有点、线、面等基本的数据结构.三维模型的网格具有图的特征，可以看作三维空间中的图.因此，通过图导出生成树，就能在三维模型对应的网格上生成迷宫.

对于给定的三维模型，三维迷宫的设计算法如图12所示.二维迷宫实体化即将迷宫由二维结构转化为三维结构，如图13(b)所示，其目的是将二维迷宫通过三维模型合成三维迷宫.通过迷宫与三维模型之间的布尔差运算实现三维迷宫的合成.布尔差运算实际上就是从原始三维模型中减去二维迷宫，得到三维迷宫，如图13(c)所示.

图12 三维迷宫设计流程Fig.12 The pipeline design of 3D maze

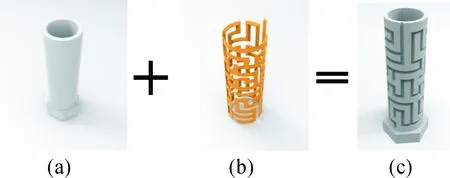
图13 三维迷宫设计Fig.13 The design of 3D maze

2.2 四边形网格化

网格是表示三维模型最简单、最有效的方式，网格化也是三维模型研究的基础.针对不同的问题需选择不同的网格化方式.本文选择三维模型的四边形网格化，如图14所示，主要基于以下考虑：

(1)高质量的四边形网格相对于自由度相同的三角形网格，具有更精确的解和较好的收敛性;

(2)四边形网格更符合二维迷宫的特征，因此生成的二维迷宫也具有较好的外观.

图14 三维模型的四边形网格Fig.14 The quadrilateral mesh of the 3D model

20世纪80年代，四边形网格化成为研究的热点.根据生成原理，四边形网格化大致可分为直接法和间接法.直接法是在给定的几何区域上直接生成四边形网格；间接法就是将三角网格转化为四边形网格.即将1个四边形沿对角线分成2个三角形.因此四边形网格可看作特殊的三角网格,反之不成立.通过移除三角网格之间的对角线，将2个三角形变成一个四边形，可得到一个既有三角形网格又有四边形网格的混合网格.

2.3 基于四边形网格的三维迷宫设计

四边形网格的结构为迷宫的生成提供了便利.首先，获取四边形网格中所有顶点的领域信息.除边界外，四边形网格顶点的邻接点数都为4.为简便，本文仅考虑在四边形网格内部生成迷宫，即顶点的邻接点个数都为4.

然后，指定迷宫的起点和终点，采用基于生成树的二维迷宫生成算法，在四边形网格表面生成二维迷宫，如图15所示.其中，(a)表示在四边形网格上选取2点作为起点和终点；(b)表示随机生成连接起点和终点的一条主路径；(c)表示在主路径基础上生成迷宫的其他支路；(d)表示不断重复此过程最终得到完整的迷宫.算法的具体过程已在前文详述，不再重复.

图15 基于四边形网格的三维迷宫设计Fig.15 The design of 3D maze based on the quadrilateral mesh

为建立三维迷宫，需将二维迷宫实体化.这里实体化指用圆柱替代迷宫中的路径.圆柱需满足以下条件：

(1)高度等于两顶点之间的距离；

(2)上下2个底面分别以相邻2个顶点为圆心；

(3)圆柱之间按照顶点顺序依次连接.

最后，将实体化的迷宫与原始的三维模型做布尔差运算，得到基于三维结构的三维迷宫模型.

3 结 果

图16显示了3种设计风格的二维迷宫.随机迷宫通过传统迷宫算法实现，循环迷宫通过本文提出的迷宫生成算法实现，定制迷宫是系统结合用户交互生成，用户可以自行设计迷宫的主路径，支路部分由系统随机生成.通过对比可以看出，定制迷宫能够产生较好的路径形状，循环迷宫左右两侧可相互连通.

图16 3种风格的二维迷宫Fig.16 Three kinds of 2D mazes

图17展示了3种复杂度的二维迷宫，根据复杂度公式，(a)图的复杂度为0，(b)图的为25.2，(c)图的为33.5.

OpenSCAD是一款编程式建模工具，可以方便地生成三维模型，本文使用该工具生成迷宫模型.3D打印作为一种个性化定制的制造工具，制造三维模型非常方便.本文使用FDM 3D打印机制造了基于圆柱面的迷宫盒，包括迷宫芯和障碍壳两部分，障碍壳中有一个小球，恰好可沿着迷宫芯中的凹槽滑动，玩家通过旋转和前后运动可将迷宫芯和障碍壳分离和合并.

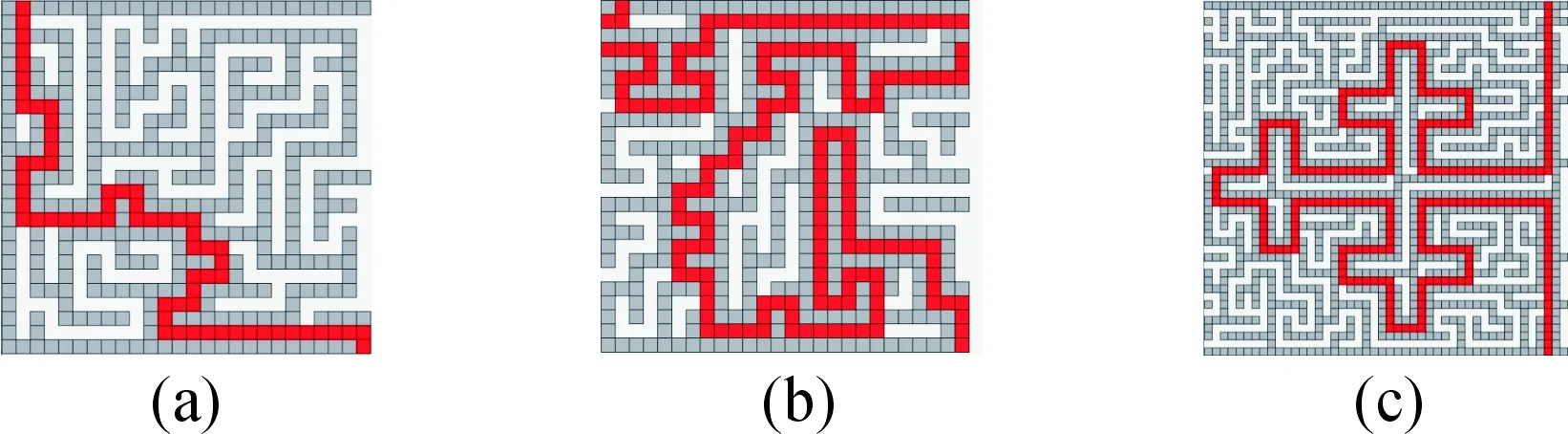
图17 不同复杂度的二维迷宫Fig.17 2D mazes with different complexities

图18(a)是生成的迷宫芯和障碍壳的三维模型，图18(b)是3D打印的迷宫盒实物.笔者还设计了基于球面的三维迷宫，如图18(c)和(d)所示.图19展示了将障碍壳与迷宫盒分离的操作过程，可以看出三维迷宫具有良好的可操作性和趣味性.本文算法可直接应用于任意网格曲面，设计曲面造型趣味十足的三维迷宫，如图20所示.

图18 三维迷宫模型及其实物Fig.18 3D maze models and material objects

图19 迷宫盒操作Fig.19 Operations of 3D maze box

图20 任意曲面的三维迷宫Fig.20 3D mazes of arbitrary surfaces

4 结 论

结合二维迷宫设计与三维模型结构，提出了一种三维迷宫设计与建模方法，设计了一种基于立体结构的三维迷宫.作为玩具，三维迷宫在平面迷宫的基础上增加了难度，同时也赋予迷宫更多的可操作性，从而大大增强了迷宫游戏的趣味性与可玩性.

首先，改进了基于生成树的传统迷宫生成算法.将迷宫的生成分为先主路径、后支路2个过程，为设计随机迷宫、循环迷宫及定制迷宫等不同风格的二维迷宫提供了便利.然后，基于生成的二维迷宫，尝试利用圆柱体和球体设计三维迷宫，通过OpenSCAD建模软件设计了基于圆柱造型、球造型的三维迷宫，并用FDM 3D打印机打印了成品.最后，将三维迷宫推广到一般曲面，经四边形网格化、网格表面设计二维迷宫、求布尔差等步骤，成功实现了一般曲面上的三维迷宫设计.

本文算法还有待进一步改进.首先，只能定制主路径迷宫，尚无法实现迷宫的完整定制.其次，在一般曲面上设计的三维迷宫的质量依赖于四边形网格化算法的质量.

[1] 余洋，张伶伶，杨晓军.“迷宫”——景观的神秘体验[J].华中建筑，2010(2):29-31. YU Y, ZHANG L L, YANG X J. “Labyrinth”: The landscape mystical experience [J]. Huazhong Architecture,2010(2):29-31.

[2] CHENG T K, XIANG L M, LYN T Y, et al. To?: journey or destination?[C]//Proceedings of the 12th International Conference on Advances in Computer Entertainment Technology. New York： ACM,2015:37.

[3] WANG D, ZHANG C, WANG H. T-maze: A tangible programming tool for children[C]//Proceedings of the 10th International Conference on Interaction Design and Children. Now York：ACM,2011:127-135.

[4] LLOTET J, KIRTON T. The maze EV: A two player installation game[C]//Proceedings of the 8th International Conference on Advances in Computer Entertainment Technology. New York：ACM,2011:1-2.

[5] HUANG T W, WU P C, WONG M D F. UI-route: An ultra-fast incremental maze routing algorithm[C]//Proceedings of SLIP (System Level Interconnect Prediction) on System Level Interconnect Prediction Workshop. New York： ACM,2014:1-8.

[6] PHILLIPS A. The topology of Roman mosaic mazes [J]. Leonardo,1993,25(3/4):65-73.

[7] MCCLENDON M S. The complexity and difficulty of a maze[C]//Bridges: Mathematical Connections in Art, Music, and Science. Bridges Conference,2001:213-222. http//archive.bridges mathart.org/2001/bridges2001-213pdf.

[8] XU J, KAPLAN C S. Vortex maze construction [J]. Journal of Mathematics and the Arts,2007,1(1):7-20.

[9] XU J, KAPLAN C S. Image-guided maze construction[J]. ACM Transactions on Graphics,2007,26(3):Article No.29.

[10] 袁开，友杨勇.平面迷宫地图随机生成树算法设计与实现[J].科学咨询，2013(1):138-139. YUAN K, YOU Y Y. Plane random tree algorithm design and implementation of maze map [J]. Scientific Consult,2013(1):138-139.

[11] 田翠花，许卫平，陈玉明.深度优先遍历算法、随机布点法及回溯法在迷宫游戏中的应用[J].河北北方学院学报，2013,29(3):19-24. TIAN C H, XU W P, CHEN Y M. Application of depth-first traversal, randomly distributed point algorithm and backtracking method to maze game [J]. Journal of Hebei North University: Natural Science Edition,2013,29(3):19-24.

[12] 严蔚敏，吴伟民.数据结构(C语言版)[M].北京：清华大学出版社，2007. YAN W M, WU W M. Data Structure (C Language Version) [M]. Beijing: Tsinghua University Press,2007.

WANG Kang, WU Wenming, LIU Ligang

(SchoolofMathematicalSciences,UniversityofScienceandTechnologyofChina,Hefei230026,China)

3D maze has reached a high level in terms of complexity and fun. By improving the algorithm of generating a 2D maze, we propose the concept of loop maze and the complexity formula of the maze. Then, an algorithm for designing a 3D maze is presented based on the quadrilateral mesh surface. This approach mainly consists of three steps: Firstly, the quadrilateral mesh is generated on the given 3D surface; Secondly, the start point and end point of the maze are chosen alternatively, and the maze on the quadrilateral mesh surface is obtained by the algorithm of generating a 2D maze which is based on a spanning tree algorithm; At last, the maze is turned into 3D structure, and 3D maze is generated by Boolean operation between the 3D structure and the original 3D model. Several personalized 3D maze toys are produced by 3D printer, which consumedly enhances fun and user experience.

3D maze; modeling; spanning tree; complexity; 3D printing

2016-07-05.

国家自然科学基金资助项目(61222206，11526212)；中科院“百人”计划项目.

王 康(1991-)，ORCID:http://orcid.org/0000-0002-6667-3131,男,硕士研究生，主要从事3D打印研究.

*通信作者，ORCID:http://orcid.org/0000-0002-2118-3016,E-mail：ligang.liu@gmail.com.

10.3785/j.issn.1008-9497.2017.02.001

TP 391

A

1008-9497(2017)02-127-07

3D maze design and modeling.Journal of Zhejiang University(Science Edition), 2017,44(2):127-133