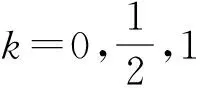基于区间数的直觉模糊多属性决策研究
段 传 庆
(1.合肥工业大学 管理学院, 安徽 合肥 230009; 2.合肥工业大学 数学学院, 安徽 合肥 230009)
基于区间数的直觉模糊多属性决策研究
段 传 庆1,2
(1.合肥工业大学 管理学院, 安徽 合肥 230009; 2.合肥工业大学 数学学院, 安徽 合肥 230009)
研究一类属性权重未知的直觉模糊多属性决策问题. 将直觉模糊数的属性值转由双区间数表示,根据决策方案属性值间的离差确定属性权重. 根据各方案属性加权综合值及区间直觉模糊数的得分函数,对2套方案分别进行排序和比较, 并通过实例说明了该方法的有效性.
直觉模糊数;区间数;多属性决策;权重
0 引 言
1965年,ZADEH[1]提出了模糊集理论,在此基础上,ATANASSOV[2]又提出了直觉模糊集概念. 直觉模糊集在模糊集理论的基础上提出了隶属度、非隶属度及犹豫度3个概念,从而更准确地反映事物的本质.但是决策者提供的信息有时很难用隶属度、非隶属度及犹豫度的精确数值来表达,而用区间数可以更方便、准确地描述其意图及想法.
受时间、空间等客观因素及自身知识结构和专业水平等主观因素的限制,决策者无法给予决策方案精确的信息. 对于属性权重的描述更是如此. 因此,如何确定属性权重一直是模糊多属性决策的热点. 熵权法是一种客观赋权法,不少学者对其进行过研究[3-8].文献[9]根据属性值的均值、方差及属性间的关联度,建立模型描述属性. 文献[10]通过集成主、客观权重求得属性综合权重. 文献[11]利用熵和离差确定属性权重,既考虑了数据本身的重要性,又兼顾到数据间的联系.关于区间数权重的确定问题, 文献[12]引入了偏差的概念,利用偏差和最小建立目标规划模型计算属性权重. 文献[13]依据主客观信息偏差最小化原则,通过构造线性模型求得属性最大、最小值,从而得到属性权重区间信息. 文献[14]运用误差传递公式确定属性的权重. 文献[15]依据相对优势度的概念对属性权重进行两两比较,从而得到了属性权重排序向量. 文献[16]将区间数转化为联系数,以确定属性权重.
直觉模糊集中的隶属度、非隶属度及犹豫度所提供的信息是点估计,在很多情况下无法准确反映决策者的真实意图. 因此,属性权重的确定及最终的方案排序很可能出现与事实不符的情况. 针对上述情况,本文将直觉模糊数转化为用2个区间数来表示,同时引入风险因子k. 而风险因子k与犹豫度相对应,反映了犹豫度对决策过程的影响. 本文所提供的转化公式既体现了隶属度、非隶属度及犹豫度在决策中的作用,又规避了点估计无法准确反映决策者意图的弊端. 利用属性值间离差最大化方法建立新模型求得属性权重.用文献[16]中主值模型的综合值及区间直觉模糊集的得分函数2套方案分别进行排序,并讨论其结果.
1 基本理论
1.1 基本定义
定义1[2]设X是一个非空集合,A={〈x,μA(x),νA(x)〉|x∈X}为直觉模糊集,其中μA(x)和νA(x)分别表示X中的元素x属于X隶属度μA:X→[0,1]和非隶属度vA:X→[0,1],且满足0≤μA(x)+vA(x)≤1,∀x∈X.此外,πA(x)=1-μA(x)-vA(x)表示X中的元素x属于X的犹豫度.
定义2[17]设X是一个给定的论域,则X上的一个区间直觉模糊集A定义为:



定义3[18-19]设a1=(μa1,νa1)和a2=(μa2,νa2)为直觉模糊数,s(a1)=μa1-νa1和s(a2)=μa2-νa2分别为a1和a2的得分函数,h(a1)=μa1+νa1和h(a2)=μa2+νa2分别为a1和a2的精确函数:
若s(a1) 若s(a1)=s(a2),则 1)若h(a1)=h(a2),则a1和a2相等,即μa1=μa2和νa2=νa1,记为a1=a2; 2)若h(a1) 3)若h(a1)>h(a2),则a1大于a2,记为a1>a2. (1) (2) (3) 1.2 区间数转化为三角函数的方法 其中: (4) 称为区间数的模; (5) 称为幅角. 1.3 将直觉模糊数转化为区间数的方法 (6) 对于效益型属性,采用公式: (7) 对于成本型属性,采用公式: (8) (9) (10) 综合考虑,则 (11) 综合2种情形,记 (12) 则M(Si)越大,Ai越优. 综上所述,给出如下算法: 步骤1 将直觉模糊矩阵R=(μij,νij)mn转化为二元区间数矩阵[[μij,μij+kπij],[νij,νij+(πij-kπij)]]mn; 步骤2 利用式(11)计算属性权重ωj; 步骤3 利用式(12)计算M(Si),并根据k的取值和M(Si)的大小对Ai进行排序; 中汕厂的订单保住了,景花厂生产稳定了。阿花说这几天我心都操干了,我要美容。天天往美容院跑,脸蛋越发俏丽,身材越发魔鬼了。周末,她来厂里晃一下,交代了工作,就开车出去了。 经计算,每个方案最终都对应2个区间数,按照其所代表的意义,这2个区间数可以理解为1个区间直觉模糊数.因此,可以按区间直觉模糊数的得分函数及k的取值情况对各个选项进行排序. 例2 某公司准备提拔一名部门经理,现有8名候选人A=(A1,A2,A3,A4,A5,A6,A7,A8)符合提拔条件.公司分别从6个方面G=(G1,G2,G3,G4,G5,G6)进行评估,并将结果以直觉模糊信息形式给出[24](见表1). 表1 直觉模糊决策矩阵Table 1 Intuitionistic fuzzy decision matrix 步骤1 由于该表中属性值均为效益型,故无需再对其进行规范化处理.将上述直觉模糊矩阵转化为二元区间数矩阵(见表2). 表2 二元区间数矩阵表Table 2 Binary interval number matrix table 属性权重,如表3所示. 表3 各属性权重值表格Table 3 Table of weight values of each attribute 步骤3 对应上述k值,分别计算M(Si),见表4. 表4 各方案的综合主值表格Table 4 Consolidated master value table for each program k=0时,选项排序为: A5>A4>A1>A7>A6>A2>A8>A3; k=1时,选项排序为: A5>A1>A4>A6>A2>A7>A8>A3. 表5 二元区间数加权综合值表格Table 5 Weighted comprehensive value table for binary interval numbers 表6 各方案综合得分值表格Table 6 Comprehensive score table k=0时,其选项排序为: A5>A4>A1>A7>A6>A2>A3>A8; A5>A4>A1>A7>A6>A2>A8>A3; k=1时,排序为: A5>A1>A4>A6>A7>A2>A8>A3. [1]ZADEHLA.Fuzzyset[J]. Information and Control,1965,8(3):338-356. [2] ATANASSOV K. Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems,1986,20(1):87-96. [3] MAO J J, YAO D B, WANG C C. A novel crossentropy and entropy measures of IFSs and their applications[J]. Knowledge-Based Systems,2013, 48:37-45. [4] 王晓杰,魏翠萍,郭婷婷.基于交叉熵和熵的直觉模糊多属性群决策专家权重的确定[J].曲阜师范大学学报,2011,37(3):35-40. WANG X J,WEI C P,GUO T T. A method to drive experts’ weights in intuitionistic fuzzy multi-attribute group decision making based on cross entropy and entropy[J]. Journal of Qufu Normal University,2011,37(3):35-40. [5] 赵萌,任嵘嵘.基于模糊熵的直觉模糊多属性群决策方法[J].数学的实践与认识,2014,44(23):153-159. ZHAO M, REN R R. Method based on fuzzy entropy with intuitionistic fuzzy set for group multi-attribute decision making[J]. Journal of Mathematics in Practice and Theory, 2014,44(23):153-159. [6] 戚晓雯,梁昌勇,张恩桥,等.基于熵最大化的区间直觉模糊多属性群决策方法[J].系统工程理论与实践,2011,31(10):1940-1948. QI X W, LIANG C Y, ZHANG E Q, et al. Approach to interval-valued intuitionistic fuzzy multiple attributes group decision making based on maximum entropy[J].Systems Engineering Theory & Practice, 2011,31(10):1940-1948. [7] 陈晓红.基于熵和关联系数的区间直觉模糊决策方法[J].系统工程与电子技术,2013,35(4):791-794. CHEN X H. Approach to interval-valued intuitionistic fuzzy decision making based on entropy and correlation coefficient[J]. Systems Engineering and Electronics,2013,35(4):791-794. [8] 李兰平.基于一类新的直觉模糊熵的直觉模糊多属性决策法[J].齐齐哈尔大学学报,2014,30(2):83-86. LI L P. Intuitionistic fuzzy multi-attribute decision making based on a new intuitionistic fuzzy entropy measure[J].Journal of Qiqihar University,2014,30(2):83-86. [9] 刘小弟,朱建军,张世涛,等.考虑属性权重优化的犹豫模糊多属性决策方法[J].控制与决策,2016,31(2):297-302. LIU X D, ZHU J J, ZHANG S T, et al. Hesitant fuzzy multiple attribute decision making method based on optimization of attribute weight[J]. Control and Decision,2016,31(2):297-302. [10] 韩二东,郭鹏,赵静.主客观权重集成及扩展VIKOR的多属性群决策方法[J].计算机工程与应用,2015,51(11):1-6. HAN E D, GUO P, ZHAO J. Method for multiple attribute group decision maling based on subjective-objective weight integrated and extended VIKOR[J].Computer Engineering and Applications, 2015,51(11):1-6. [11] 段传庆.一种对方案有偏好的区间直觉模糊多属性算法[J].中国科学技术大学学报,2015,45(12):100-105. DUAN C Q. Approach to interval-valued intuitionistic fuzzy multiple attribute decision making with preference information[J].Journal of University of Science and Technology of China, 2015,45(12):100-105. [12] XU Z S. Multiple attribute group decision making with different formats of preference information on attributes[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B,2007,37:1500-1511. [13] XU Z S, CHEN J. MAGDM linear programming models with distinct uncertain preference structures[J]. IEEE Transactions on Systems,Man,and Cyber-netics-Part B,2008,38:1356-1370. [14] YOON K. The propagation of errors in multiple-attribute decision analysis:A practical approach[J]. Journal of the Operational Research Society,1989, 40(7): 681-686. [15] 张吉军. 区间数多指标决策问题的模糊层次分析法[J]. 工业工程与管理,2003(6):20-23. ZHANG J J. Fuzzy AHP in multiple attribute decision making with interval numbers[J]. Industrial Engineering and Management,2003(6):20-23. [16] 刘秀梅,赵克勤. 基于联系数的属性权重未知的区间数多属性决策研究[J]. 数学的实践与认识,2013,43(3):143-148. LIU X M, ZHAO K Q. Interval multi-attribute decision making with the attribute weight unknown based on connection number[J]. Journal of Mathematics in Practice and Theory, 2013,43(3):143-148. [17] ATANASSOV K, GARGOV G. Interval-valued intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems,1989,31(3):343-349. [18] XU Z S. Intuitionistic fuzzy aggregation operators [J]. IEEE Transactions on Fuzzy Systems,2007,15(6):1179-1187. [19] XU Z S, YAGER R R. Some geometric aggregation operators based on intuitionistic fuzzy sets[J]. International Journal of General Systems,2006,35(4):417-433. [20] 徐泽水.区间直觉模糊信息的集成方法及其在决策中的应用[J].控制与决策,2007,22(2):215-219. XU Z S. Methods for aggregating interval-valued intuitionistic fuzzy information and their application to decision making [J]. Control and Decision,2007,22(2):215-219. [21] 徐泽水.不确定多属性决策方法及应用[M].北京:清华大学出版社,2004:105-117. XU Z S. Uncertain Multiple Attribute Decision Making:Methods and Applications[M]. Beijing: Tsinghua University Press,2004:105-117. [22] 刘秀梅,赵克勤.基于联系数复运算的区间数多属性决策方法及应用[J].数学的实践与认识,2008,38(23):57-64. LIU X M, ZHAO K Q. Multiple attribute decision making and its applications based on complex number arithmetic operation of connection number with interval numbers[J]. Journal of Mathematics in Practice and Theory,2008,38(23):57-64. [23] XU Z S, HU H. Projection models for intuitionistic fuzzy multiple decision making[J]. International Journal of Information Technology and Decision Making,2010,9(2):267-280. [24] 王翠翠,姚登宝,毛军军,等.基于熵和相关系数的直觉模糊多属性决策方法[J].计算机应用,2012,32(11):3002-3004. WANG C C, YAO D B, MAO J J, et al. Intuitionistic fuzzy multiple attributes decision making method based on entropy and correlation coefficient[J]. Journal of Computer Applications,2012,32(11):3002-3004. DUAN Chuanqing1,2 (1.SchoolofBusinessAdministration,HefeiUniversityofTechnology,Hefei230009,China; 2.SchoolofMathematics,HefeiUniversityofTechnology,Hefei230009,China) This paper discusses the multiple attribute decision making problems, in which the information about attribute weights is totally unknown and the attribute values are expressed by intuitionistic fuzzy sets. Two interval numbers are used to take the place of attribute values. A new method is proposed to gain the weights of the attributes based on the deviations between the values of the attributes. We make the ranking of projects by the weighted comprehensive values of all projects and the score function of interval-valued intuitionistic fuzzy numbers, respectively, and then compared with the results of the two methods. Finally,an illustrative example is given to verify the effectiveness of the method. intuitionistic fuzzy number; interval number;multiple attribute decision making;entropy 2016-05-19. 中央高校基本科研业务费专项资金资助(J2014HGXJ0080). 段传庆(1978-),ORCID:http://orcid.org/0000-0002-3096-3479,男,博士,讲师,主要从事决策分析研究,E-mail:dcqhn@126.com. 10.3785/j.issn.1008-9497.2017.02.009 C 934 A 1008-9497(2017)02-174-07 Intuitionistic fuzzy multiple attribute decision making based on interval numbers. Journal of Zhejiang University(Science Edition), 2017,44(2):174-180



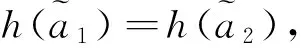





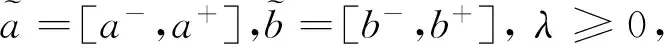



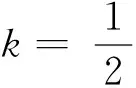
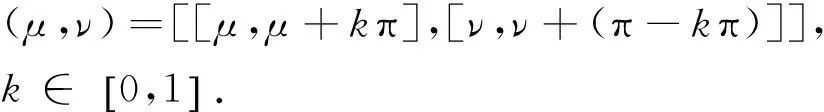
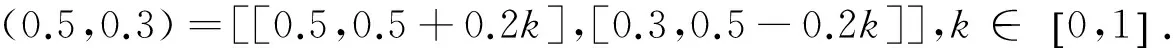
2 决策方法
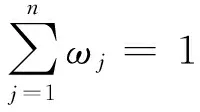



3 算例分析








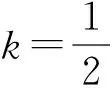
4 结果比较
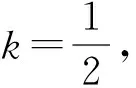


5 结 论