含无关项布尔函数的对称变量检测算法
张永波,厉晓华
(1.浙江旅游职业学院 信息中心, 浙江 杭州 311231; 2.浙江大学 信息中心, 浙江 杭州 310027)
含无关项布尔函数的对称变量检测算法
张永波1,厉晓华2*
(1.浙江旅游职业学院 信息中心, 浙江 杭州 311231; 2.浙江大学 信息中心, 浙江 杭州 310027)
为简化布尔函数中12类对称变量的检测过程,提出了含无关项布尔函数基于最小项展开系数的对称变量检测算法. 该算法通过判别布尔函数有序特征值矩阵的约束条件以实现对称变量的快速检测. 应用结果表明,与现有方法相比,算法在适用的布尔函数变量数、检测类型、检测含无关项布尔函数和检测过程的复杂度方面表现较优.
对称变量;有序特征值矩阵;布尔函数;真值表;任意项
0 引 言

1 布尔函数最小项展开式
任意n变量含无关项布尔函数的最小项展开式表示为[6]:
(1)
di∈{0,1}表示无关项系数,di=0表示mi不属于无关项,di=1表示mi属于无关项,di,mi不同时为1.
2 对称变量检测方法
2.1 相关定义
根据文献[7],布尔函数存在6类对称变量和6类反对称变量,其定义如表1和2所示.
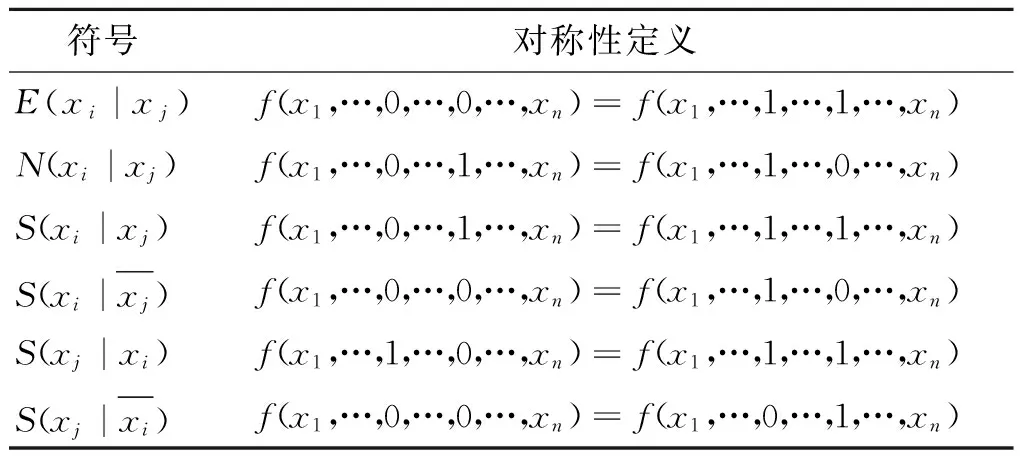
表1 6类对称变量Table 1 Six types of symmetry

表2 6类反对称变量Table 2 Six types of antisymmetry
定义1 最小项展开系数矩阵
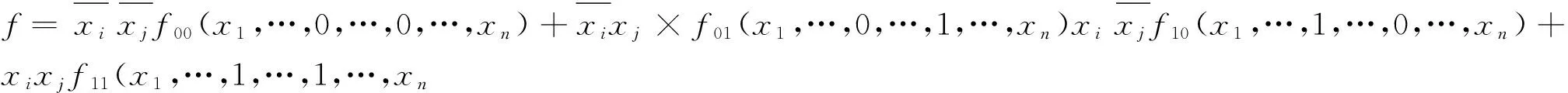
若将展开式中子函数f00(x1,…,0,…,0,…,xn),f01(x1,…,0,…,1,…,xn),f10(x1,…,1,…,0,…,xn),f11(x1,…,1,…,1,…,xn)的最小项展开系数ai按下标i升序排列组成有序矩阵,该有序矩阵称为子函数的最小项展开系数矩阵,分别表示为C0,C1,C2,C3.
定义2 当逻辑变量xixj取值00,01,10,11时,布尔函数真值表中的相应最小项展开系数称为真值表的特征值.
定义3 当逻辑变量xixj取00,01,10,11不同值时,该变量编码称为xixj的特征编码.
定义4 若将真值表的特征值ai按下标i升序排列组成有序矩阵,则该矩阵称为有序特征值矩阵,表示为[ai]xixj. 当逻辑变量xixj取值00,01,10,11时,[ai]xixj可表示为[ai]00,[ai]01,[ai]10,[ai]11.
由定义1~3可知,C0,C1,C2,C3和[ai]xixj满足如下关系:
C0=[ai]00,C1=[ai]01,C2=[ai]10,C3=[ai]11.
定义5 矩阵A、B异或运算就是对2个矩阵中的相应元素进行异或操作.
若A=[a1…ai…an],B=[b1…bi…bn],
则A⊕B=[a1⊕b1…ai⊕bi…an⊕bn].
定义6 在有序特征值矩阵中,除无关项之外的所有元素均称为决定性元素.
2.2 算法原理
定理1 若n变量布尔函数f(x1,…,xi,…,xj,…xn)的有序特征值矩阵[ai]xixj中的决定性元素异或运算结果满足表3的约束条件,则该布尔函数存在相应的对称变量.
证明 以[ai]xixj约束条件[ai]00⊕[ai]11=[000…0]为例,根据异或运算的性质,无关性与0、1、无关项之间的异或运算结果如表4所示. 矩阵[ai]00、[ai]11进行异或运算时,只需考虑决定性元素.
若n变量布尔函数f(x1,…,xi,…,xj,…xn)的有序特征值矩阵[ai]xixj满足[ai]00⊕[ai]11=[000…0],则有
C0⊕C3=[000…0].
(2)
式(2)可改写为:
C0⊕C3⊕C3=[000…0]⊕C3,
C0⊕(C3⊕C3)=C3,
C0⊕[000…0]=C3,
C0=C3,
所以f(x1,…,0,…,0,…,xn)=f(x1,…,1,…,1,…,xn). 由表1的定义可知,该布尔函数存在E(xi|xj)类对称变量.
同理,可证得表3中其他11类对称变量.

表3 逻辑变量对称条件Table 3 The symmetric conditions of logical variables

表4 异或运算Table 4 The exclusive operation
由上述讨论可知,基于有序特征值矩阵检测含无关项布尔函数12类对称变量的过程如下:
(1)列出布尔函数的真值表.
(2)根据真值表得到[ai]xixj.
(3)对[ai]xixj中的无关项元素略去异或运算,判断[ai]xixj是否满足表3的元素条件.
2.3 算法实例
例1 三变量布尔函数f1(x1,x2,x3)=∑m(0,2,5,6)+d(7),应用有序特征值矩阵方法检测对称变量.
由函数f1(x1,x2,x3)的真值表(见表5)可得[ai]x1x2:
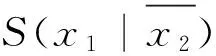
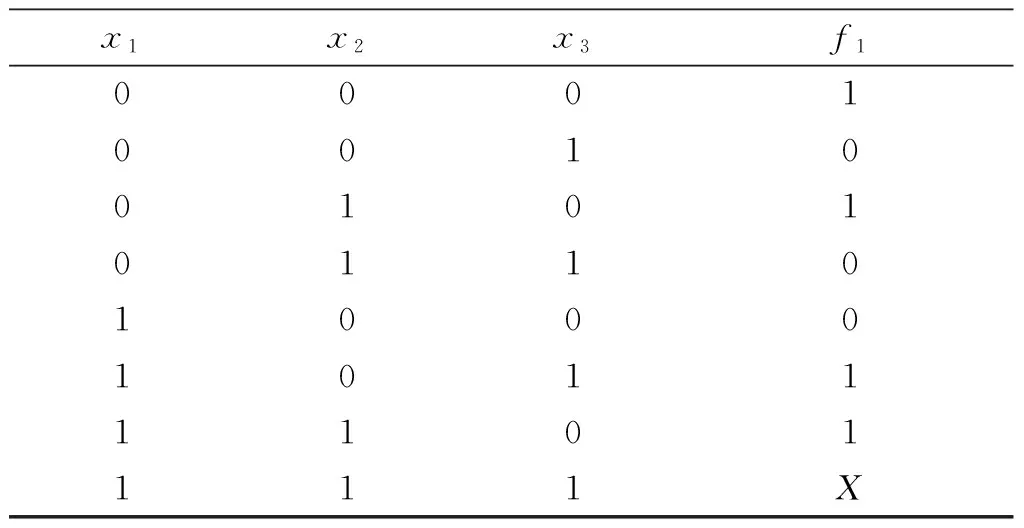
表5 布尔函数f1的真值表Table 5 The truth table of f1

2.4 算法实现
步骤1 定义二维数组y,用于保存被检测函数. 数组y存在2n行和n+1列. 前n行保存f(x1~xn)的变量编码,最后一行保存被检测函数的最小项展开系数. 以本文2.3节中的例1为例,得到的二维数组y1如表6所示.
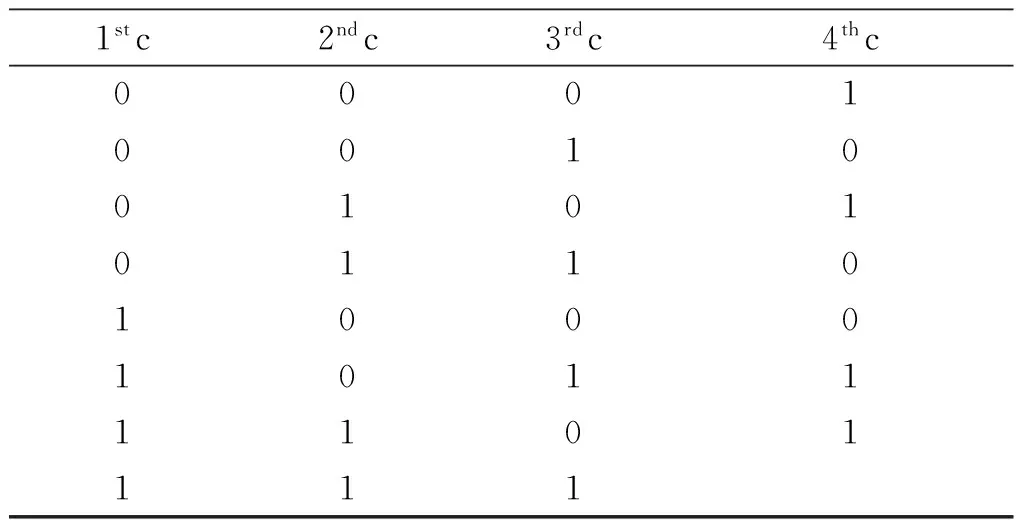
表6 二维数组y1Table 6 Representation of columns of array y1
步骤2 定义一维数组C0,C1,C2,C3. 任意选择数组y中的两列,即逻辑变量xi、xj(1≤i (1)若y[k][i]=0,y[k][j]=0,则将y[k][n+1]的值保存于数组C0. (2)若y[k][i]=0,y[k][j]=1,则将y[k][n+1]的值保存于数组C1. (3)若y[k][i]=1,y[k][j]=0,则将y[k][n+1]的值保存于数组C2. (4)若y[k][i]=1,y[k][j]=1,则将y[k][n+1]的值保存于数组C3. 步骤3 判断数组C0,C1,C2,C3中的值: (1)对数组C0,C3中的相应元素进行异或运算,当相应元素出现空格值时,运算结果为空格值. 若非空格值元素的运算结果都等于0,则输出E(xi|xj);若非空格值元素的运算结果都等于1,则输出CE(xi|xj). (2)数组C1,C2中的相应元素进行异或运算,当相应元素出现空格值时,运算结果为空格值. 若非空格值元素的运算结果都等于0,则输出N(xi|xj);若非空格值元素的运算结果都等于1,则输出CN(xi|xj). (3)数组C1,C3中的相应元素进行异或运算,当相应元素出现空格值时,运算结果为空格值. 若非空格值元素的运算结果都等于0,则输出S(xi|xj);若非空格值元素的运算结果都等于1,则输出CS(xi|xj). (5)数组C2,C3中的相应元素进行异或运算,当相应元素出现空格值时,运算结果为空格值. 若非空格值元素的运算结果都等于0,则输出S(xj|xi);若非空格值元素的运算结果都等于1,则输出CS(xj|xi). 步骤5 终止循环. 程序流程图如图1所示. 图1 程序流程图Fig.1 The flow chart of the program 不同检测方法之间的性能比较见表7. 图形方法、谱系数方法、表格方法、快速算法都不适用于含无关项布尔函数. 若被检测布尔函数含无关项,新算法明显是最优的; 若被检测函数不包含无关项,新算法在布尔函数的适用变量数、检测类型、检测过程复杂度方面也最有效. 表7 5种方法比较Table 7 Comparison of five methods 注n表示布尔函数变量数. 提出了含任意项布尔函数的对称变量检测算法,该算法同样适用于不含任意项的布尔函数,为构造密码学函数和简化电路设计奠定了基础. [1] RICE J, MUZIO J. Antisymmetries in the realization of Boolean functions[C]//IEEE International Symposium on Circuits and Systems. Phoenix, AZ: IEEE,2002:69-72. [2] BLAIS E, WEINSTEIN A, YOSHIDA Y. Partially symmetric functions are efficiently isomorphism-testable[C]// IEEE 53rd Anual Smposium on Fundation of Computer Science.Washington: IEEE,2012:551-560. [3] PENG J, WU Q, KAN H. On symmetric Boolean functions with high algebraic immunity on even number of variables[J]. IEEE Transations on Information Theory,2011,57(10):7205-7220. [4] WANG H, PENG J. On 2k-variable symmetric Boolean functions with maximum algebraic immunity[J]. IEEE Transations on Information Theory,2012,58(8):5612-5624. [5] MUKHOPADHYAY A. Detection of total or partial symmetry of a switching function with the use of decomposition charts[J]. IEEE Transations on Electronic Computers,1963,EC(12):553-557. [6] HURST S L. Detection of symmetries in combinatorial functions by spectral means[J]. Electronic Circuits and System,1977,1(5):173-180. [7] KANNURAO S, FALKOWSKI B. Identification of complement single variable symmetry in Boolean functions through Walsh transform[C]// IEEE International Symposium on Circuits and Systems. Phoenix, AE: IEEE,2002:745-748. [8] 练益群,厉晓华,陈偕雄.基于表格法的部分对称函数检测[J].科技通报,2005,21(2):214-217. LIAN Y Q, LI X H, CHEN X X. Detection of partial symmetric functions based on tabular method[J]. Bulletin of Science and Technology,2005,21(2):214-217. [9] 厉晓华,杭国强,陈偕雄.逻辑函数对称变量检测算法[J].电路与系统学报,2013,18(2):31-35. LI X H, HANG G Q, CHEN X X. The algorithm for identifying symmetric variable of logical function[J]. Journal of Circuits and Systems,2013,18(2):31-35. ZHANG Yongbo1, LI Xiaohua2 (1.CampusInformationCenter,TourismCollegeofZhejiang,Hangzhou311231,China;2.CampusInformationCenterofZhejiangUniversity,Hangzhou310027,China) To simplify the process for identifying 12 types of symmetric variables in Boolean function, we propose a new symmetry detection algorithm based on minterm expansion of Boolean function with don’t-care-terms. By analyzing the constraint conditions of the order eigenvalues matrixes for 12 types of symmetric variables, the algorithm for identifying symmetric variables of Boolean function with don’t-care-terms is proposed. The results show that, the new algorithm method is superior than the traditional methods in the applicability of the number of logical variables of Boolean function including don’t-care-terms, detection types, and complexity of the identification process. symmetric variable;the order eigenvalues matrix;Boolean function;truth table;don’t-care-terms 2016-05-19. 国家自然科学基金资助项目(61471314);浙江省公益技术研究社会发展项目(2014C33042). 张永波(1970-),ORCID:http://orcid.org/0000-0001-9529-3851,男,高级工程师,主要从事计算机应用与网络信息安全研究. *通信作者,ORCID:http://orcid.org/0000-0003-2482-9000,E-mail:xiaohua@zju.edu.cn. 10.3785/j.issn.1008-9497.2017.02.011 TN 431 A 1008-9497(2017)02-186-05 An algorithm for identifying symmetric variables of Boolean function with don’t-care-terms. Journal of Zhejiang University(Science Edition), 2017,44(2):186-190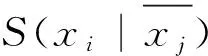
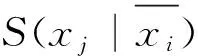

3 不同检测方法的比较

4 结 论


