弱entwining结构的cup积

史 美 华

(浙江外国语学院， 浙江 杭州 310012)

弱entwining结构的cup积

史 美 华

(浙江外国语学院， 浙江 杭州 310012)

给出了弱entwining结构上同调的2种cup积，并证明了它们都是求导度为1的分次结合代数，同时证明了弱entwining结构的复形是弱comp代数，利用其结论得到了2种cup积结构的关系，推广了双代数的Gerstenhaber-Schack理论.

弱entwining结构；弱comp代数；cup积

本文首先给出了弱entwining结构上同调的2种cup积，并证明其均匀求导度为1的分次结合代数.其次，证明了弱entwining结构的复形是弱comp代数，并利用其结论得到了2种cup积结构的关系，从而推广了双代数的Gerstenhaber-Schack理论.

由文献[3]知，一个域k上的弱entwining结构(A,C,ψ)是由代数A、余代数C和k-线性映射ψ:C⊗A→A⊗C,c⊗a→∑aψ⊗cψ组成，并且对∀a,b∈A,c∈C满足：

∑(ab)ψ⊗cψ=∑aψbφ⊗cψφ;

(1)

∑aψ⊗cψ1⊗cψ2=∑aψφ⊗c1φ⊗c2ψ;

(2)

∑1ψ⊗cψ=∑1ψε(c1ψ)⊗c2;

(3)

∑aψε(cψ)=∑1ψaε(cψ).

(4)

当一个弱entwining映射ψ在同一个式子中多次出现时，分别用符号ψ1,ψ2,...,δ,θ,...等表示.若1ψ⊗cψ=1⊗c，则弱entwining结构就是entwining结构.

(5)

(6)

(7)

(8)

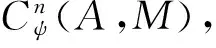
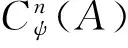
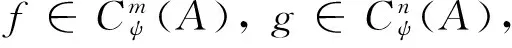
∑1ψf(cψ2⊗a1⊗…⊗am)φ×

g(cψ1φ⊗am+1⊗…⊗am+n)=

∑1ψδf(c2ψ⊗a1⊗…⊗am)φ×

g(c1δφ⊗am+1⊗…⊗am+n);

∑1ψ(1δf(cψ2δ⊗a1⊗…⊗am))φ×

g(cψ1φ⊗am+1⊗…⊗am+n)=

∑1ψ1δθf(cψ2δ⊗a1⊗…⊗am)φ×

g(cψ1θφ⊗am+1⊗…⊗am+n)=

∑1ψϖ1δθf(c2ψδ⊗a1⊗…⊗am)φ×

g(c1ϖθφ⊗am+1⊗…⊗am+n)=

∑(1ψ1δ)θf(c2ψδ⊗a1⊗…⊗am)φ×

g(c1θφ⊗am+1⊗…⊗am+n)=

∑1ψθf(c2ψ⊗a1⊗…⊗am)φ×

g(c1θφ⊗am+1⊗…⊗am+n);

∑1ψf(cψ2⊗a1⊗…⊗am)φ1δ×

g(cψ1φδ⊗am+1⊗…⊗am+n)=

∑1ψf(cψ2⊗a1⊗…⊗am)φ×

g(cψ1φ⊗am+1⊗…⊗am+n)=

∑1ψθf(c2ψ⊗a1⊗…⊗am)φ×

∑(f(c3⊗a1⊗…⊗am)δ×

g(c2δ⊗am+1⊗…⊗am+n))φ×

h(c1φ⊗am+n+1⊗…⊗am+n+l)=

∑f(c3⊗a1⊗…⊗am)δφ×

g(c2δ⊗am+1⊗…⊗am+n)ψ×

h(c1φψ⊗am+n+1⊗…⊗am+n+l)=

(c1δ⊗am+1⊗…⊗am+n+l)=

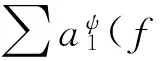
a1⊗…⊗am+n)am+n+1=

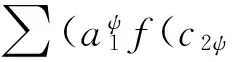
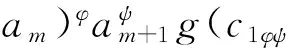
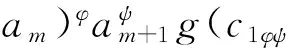
显然，定义1中的式(6)成立.

∑f(c1⊗a1φ1ψ1⊗…⊗aiφiψi⊗g(c2ψ1...ψi⊗ai+1φi+1⊗…⊗ajφj⊗h(c3φ1...φj⊗aj+i⊗…⊗aj+l)⊗an+l+i-1)⊗an+l+i⊗…⊗am+n+l-2);

∑f(c1⊗a1φ1⊗…⊗aiφi⊗g(c2φ1...φi1⊗ai+1φi+1⊗…⊗ajφj⊗h(c2φ1...φi2φi+1...φj⊗aj+i⊗…⊗aj+l)⊗an+l+i-1)⊗an+l+i⊗…⊗am+n+l-2)=

∑f(c1⊗a1φ1ψ1⊗…⊗aiφiψi⊗g(c2ψ1...ψi⊗ai+1φi+1⊗…⊗ajφj⊗h(c3φ1...φj⊗aj+i⊗…⊗aj+l)⊗an+l+i-1)⊗an+l+i⊗…⊗am+n+l-2),

因此，式(7)成立.

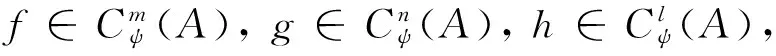
∑ε(c3φ1...φjδ)f(c1⊗a1φ1ψ1⊗…⊗ajφjψj⊗(1δaj+1aj+2)ψj+1⊗aj+3ψj+3⊗…⊗ai+1ψi+1⊗g(c2ψ1...ψi+1⊗ai+2⊗…⊗an+i+1)⊗an+i+2⊗am+n)=

∑f(c1⊗a1φ1⊗…⊗ajφj⊗1δaj+1ψj+1aj+2ψj+2⊗aj+3ψj+3⊗…⊗ai+1ψi+1⊗g(c2φ1...φjδψj+1...ψi+1⊗ai+2⊗…⊗an+i+1)⊗an+i+2⊗am+n);

∑f(c1⊗a1φ1ψ1⊗…⊗ajφjψj⊗π(c2ψ1...ψj⊗aj+1φj+1⊗aj+2φj+2)⊗g(c3φ1...φi+1⊗ai+2⊗…⊗an+i+1)⊗an+i+2⊗…⊗am+n)=

∑ε(c2φ1...φj1δ)f(c1⊗a1φ1⊗…⊗ajφj⊗1δaj+1φj+1aj+2φj+2⊗g(c2φ1...φj2φj+1...φi+1⊗ai+2⊗…⊗an+i+1)⊗an+i+2⊗…⊗am+n)=

∑f(c1⊗a1φ1⊗…⊗ajφj⊗1δaj+1ψj+1aj+2ψj+2⊗aj+3ψj+3⊗…⊗ai+1ψi+1⊗g(c2φ1...φjδψj+1...ψi+1⊗ai+2⊗…⊗an+i+1)⊗an+i+2⊗am+n),

由定理1，直接可得本文的一个主要结论，同时也是双代数Gerstenhaber-Schack理论[6-7]中经典结论的推广.

由推论1可得

(δm+n(δm(f)∝g))(c⊗a1⊗…⊗am+n)=

∑1φ1ψf(cφ1ψ⊗a1ψ1⊗…⊗amψm)g(cφ2ψ1...ψm⊗am+1⊗…⊗am+n)=

∑1φδ1ψf(c1δψ⊗a1ψ1⊗…⊗amψm)g(c2φψ1...ψm⊗am+1⊗…⊗am+n)=

∑1φψf(c1ψ⊗a1ψ1⊗…⊗amψm)g(c2φψ1...ψm⊗am+1⊗…⊗am+n)=

∑1φf(cφ1⊗a1ψ1⊗…⊗amψm)g(cφ2ψ1...ψm⊗am+1⊗…⊗am+n)=

δm+n(f∝g)(c⊗a1⊗…⊗am+n);

δm+n(f∝δn(g))(c⊗a1⊗…⊗am+n)=

∑1φf(cφ1⊗a1ψ1⊗…⊗amψm)1δg(cφ2ψ1...ψmδ⊗am+1⊗…⊗am+n)=

∑1φf(cφ1⊗a1ψ1⊗…⊗amψm)(1·g)(cφ2ψ1...ψm⊗am+1⊗…⊗am+n)=

∑1φf(cφ1⊗a1ψ1⊗…⊗amψm)g(cφ2ψ1...ψm⊗am+1⊗…⊗am+n)=

δm+n(f∝g)(c⊗a1⊗…⊗am+n),

因此，δm+n(f∝g)=δm+n(f∝δn(g))=δm+n(δm(f)∝g).

(f∝(g∝h))(c⊗a1⊗…⊗am+n+l)=

∑f(c1⊗a1ψ1⊗…⊗amψm)(g∝h)(c2ψ1...ψm⊗am+1⊗…⊗am+n+l)=

∑f(c1⊗a1ψ1⊗…⊗amψm)g(c2ψ1...ψm1⊗am+1φ1⊗…⊗am+nφn)h(c2ψ1...ψm2φ1...φn⊗am+n+1⊗…⊗am+n+l)=

∑f(c1⊗a1ψ1δ1⊗…⊗amψmδm)g(c2δ1...δm⊗am+1φ1⊗…⊗am+nφn)h(c3ψ1...ψmφ1...φn⊗am+n+1⊗…⊗am+n+l)=∑(f∝g)(c1⊗a1ψ1⊗…⊗am+nψm+n)h(c2ψ1...ψm+n⊗am+n+1⊗…⊗am+n+l)=

((f∝g)∝h)(c⊗a1⊗…⊗am+n+l),

这里，反复利用了式(2).

(df∝g)(c⊗a1⊗…⊗am+n+1)=

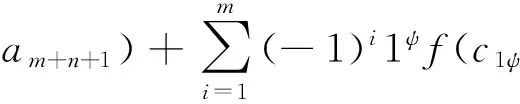
(-1)m(f∝dg)(c⊗a1⊗…⊗am+n+1)=

d(f∝g)(c⊗a1⊗…⊗am+n+1)=

…⊗amδm)g(c2ζδ1...δm⊗am+1⊗…⊗aiai+1⊗…⊗am+n+1)+(-1)m+n+11ϖσf(c1σ⊗a1δ1⊗…⊗amδm)g(c2ϖδ1...δm⊗am+1⊗…⊗am+n)am+n+1=

这里，反复利用了式(2)和(3).于是d(f∝g)=df∝g+(-1)mf∝dg.定理4证毕.

[1]BRZEZISKIT,MAJIDS.Coalgebrabundles[J]. Comm Math Phys,1998,191(2):517-522.

[3] CAENEPEEL S, GROOT E D. Modules over weak entwining structures[J]. Contemp Math,2000,267:31-54.

[4] 贾玲,李方.弱entwining结构的上同调[J].中国科学A辑:数学,2007,37(1):55-63. JIA L, LI F. Weak entwining structure of cohomology[J]. Science in China: Ser A,2007,37(1):55-63.

[5] 贾玲,李方.弱entwined模的Frobenius性质和Maschke型定理[J].数学学报,2007,50(1):105-117. JIA L, LI F. Frobenius properties and Maschke type theorems for weak entwining modules[J].Acta Mathematica Sinica,2007,50(1):105-117.

[6] GERSTENHABER M. The cohomology structure of an associative ring[J]. Ann Math,1964,79:59-103.

[7] GERSTENHABER M, SCHACK S D. Bialgebra cohomology, deformations and quantum group[J]. Procl Natl Acad Sci,1990,87:478-481.

SHI Meihua

(ZhejiangInternationalStudiesUniversity,Hangzhou310012,China)

This paper introduces two kinds of cup products of the homological over a weak entwining structure, and proves that they are both graded associative algebras of degree 1. Then, we state that complexes of weak entwining structures are weak comp algebras, which obtains the relations of the two cup products. And, the classical Gerstenhaber-Schack theory is extended.

weak entwining structure; weak comp algebra; cup product

2014-10-12.

史美华(1963-)，ORCID:http://orcid.org/0000-0002-6151-2494，女，教授，主要从事Hopf代数研究,E-mail,shimeihua63@163.com.

10.3785/j.issn.1008-9497.2017.02.003

O 153

A

1008-9497(2017)02-139-05

The cup products of a weak entwining structure. Journal of Zhejiang University(Science Edition), 2017,44(2):139-143