Cat弱Hopf代数

陈 笑 缘

(浙江商业职业技术学院， 浙江 杭州 310053 )

Cat弱Hopf代数

陈 笑 缘

(浙江商业职业技术学院， 浙江 杭州 310053 )

首先引入pre-cat弱Hopf代数和cat弱Hopf代数来刻画具有投射的弱Hopf代数的性质，并建立pre-cat弱Hopf代数的张量范畴，证明了pre-cat弱Hopf代数是cat弱Hopf代数的充要条件，从而推广了LODAY引入的cat-群和cat Hopf代数的相应结论.

弱Hopf代数；投射；cat 弱Hopf代数

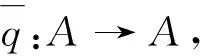
定义1 范畴C的一个fork是指图

(1)

其中，f°i=g°i.fork可分指在范畴C中存在态射h:B→A和p:A→I满足h°f=idA,h°g=i°p及p°i=idI.

例1 下式是可分fork，

(2)

∑af(11)SA(fg(f(12)))=

∑af(11)SA(f(12))=a;

∑a1f(SH(g(a2))g(a3)l)=

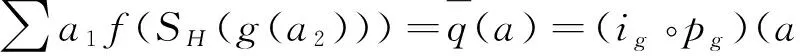
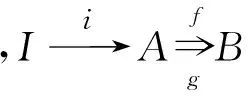
证明 定义I的代数、余代数和对极分别为μI(x⊗y)=x·y=p(i(x)i(y)),ηI=p(1A),ΔI(x)=∑p(i(x)1)⊗p(i(x)2),εI(x)=ε(i(x)),SI(x)=pSA(i(x)).

首先，验证I是一个代数且i是代数同态.事实上，对任意x,y,z∈I，有

(x·y)·z=p(h(gi(x)gi(y))i(z))=

p(h(fi(x)fi(y))i(z))=p((i(x)i(y))i(z))=

p(i(x)(i(y)i(z)))=x·(y·z);

x·p(1)=p(i(x)ip(1))=p(i(x)hg(1))=

p(i(x))=x;

i(x·y)=h(gi(x)gi(y))=h(fi(x)fi(y))=

hf(i(x)i(y))=i(x)i(y);

i(1I)=ip(1A)=hg(1A)=hf(1A)=1A.

其次，ΔI显然是余结合的且εI(1I)=ε(i(1A))=1.并且i是余代数同态，因为对任意x∈I有

(i⊗i)ΔI(x)=∑ip(i(x)1)⊗ip(i(x)2)=

∑h(gi(x)1)⊗h(gi(x)2)=∑hf(i(x)1)⊗

hf(i(x)2)=∑i(x)1⊗i(x)2.

所以只需验证I是一个弱双代数.因为对任意x,y,z∈I，有

ΔI(x)·ΔI(y)=∑p(h(gi(x)1gi(y)1))⊗p(h(gi(x)2gi(y)2))=∑p(hf(i(x)1)hf(i(y)1))⊗p(hf(i(x)2)hf(i(y)2))=∑p(i(x)1i(y)1)⊗p(i(x)2i(y)2)=ΔI(x·y);

εI(x·y1)εI(y2·z)=∑εA(h(g(i(x))gip(i(y)1)))εA(h(gip(i(y)2))gi(z))=∑εA(hf(i(x)ip(i(y)1)))εA(hf(ip(i(y)2)i(z)))=

∑εA(i(x)i(y)1)εA(i(y)2i(z))=

εA(i(x)i(y)i(z))=εI(x·y·z).

同理可证εI(x·y2)εI(y1·z)=εI(x·y·z).

(ΔI(p(1))⊗p(1))·(p(1)⊗ΔI(p(1)))=

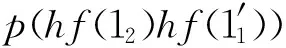
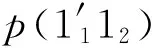
(p(1)⊗ΔI(p(1)))·(ΔI(p(1))⊗p(1)).

最后，证明I是弱Hopf代数，i是弱Hopf代数同态.实际上，对任意x∈I，有

∑SI(x1)·x2·SI(x3)=

∑p(ip(SA(i(x1))i(x2))ip(SA(i(x3))))=

∑p(h(SB(gi(x1))gi(x2))hSB(gi(x3)))=

∑p(hf(SA(i(x1))i(x2))hf(SA(i(x3))))=

∑p(SA(i(x1))i(x2)SA(i(x3)))=

p(SA(i(x)))=SI(x);

i(SI(x))=ip(SA(i(x)))=hSA(gi(x))=hf(SA(i(x)))=SA(i(x));

∑x1·SI(x2)=

∑p(ip(i(x)1)ip(SA(ip(i(x)2))))=

∑p(i(x1)hSB(gi(x2)))=

∑p(i(x1)hf(SA(i(x2)))=

∑p(i(x1)SA(i(x2))=p(i(x)l);

∑εI(p(1)1·x)p(1)2=

∑εA(ip(11)i(x))p(12)=

∑εA(11i(x))p(12)=p(i(x)l),

因此，x1·SI(x2)=∑εI(p(1)1·x)p(1)2.同理可证SI(x1)·x2=∑εI(x·p(1)2)p(1)1.证毕.

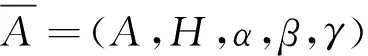
α°γ=β°γ=idH;

(3)

∑α(a2)⊗a1=∑α(a1)⊗a2,a∈A;

(4)

∑β(a2)⊗a1=∑β(a1)⊗a2,a∈A.

(5)

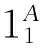
(6)

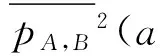
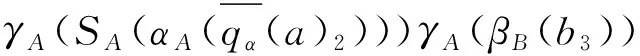
γA(βB(b1)lβB(b2))⊗b3=

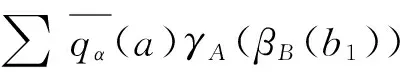
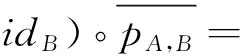
∑a1γA(SH(αA(a4)))1γA(βB(b1))⊗αA(a2γA(SH(αA(a4)))2)βB(b2)⊗b3=

∑a1γA(SH(12αA(a2)))γA(βB(b1))⊗SH(11)βB(b2)⊗b3=

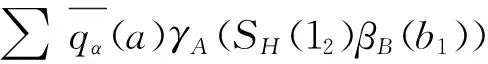
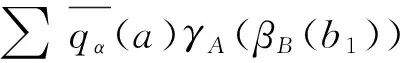
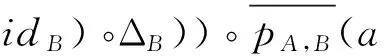
hA,B°(idA⊗((βB⊗idB)°ΔB))(a⊗b)=

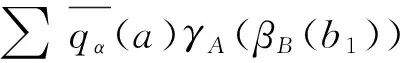
hA,B°(((idA⊗αA)°ΔA)⊗idB)(a⊗b)=

∑a11γA(SH(αA(12)))⊗b=

∑aγA(11)γA(SH(αA(γA(12))))⊗b=a⊗b.

显然，映射((idA⊗αA)°ΔA)⊗idB和idA⊗((βB⊗idB)°ΔB)均为弱Hopf代数同态，由定理1可知A⊗HB是弱Hopf代数.

最后，验证A⊗HB是pre-cat弱Hopf代数.定义2中的条件(4)和(5)显然成立，只需证明条件(3)成立.因为对任意h∈H，有

(βA⊗εB)°iA,B°γA⊗HB(h)=

∑βA(γA(h1))βAγA(SH(αA(γA(h2))))h3=

∑h1SH(h2)h3=h.

定理2证毕.

范畴CH的对象是H上的pre-cat弱Hopf代数，态射是pre-cat弱Hopf代数同态.则有以下结论.

定理3 范畴CH是monoidal范畴.

φX=(idX⊗αX)°ΔX,ψX=(βX⊗idX)°ΔX):

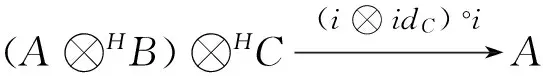
A⊗H⊗B⊗H⊗C,

(7)

A⊗H⊗B⊗H⊗C.

(8)

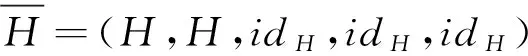
(9)

(10)

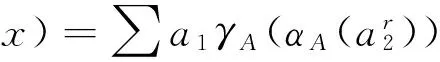
∑a1γA(SH(12αA(a2)))γA(x1)⊗SH(11)x2=

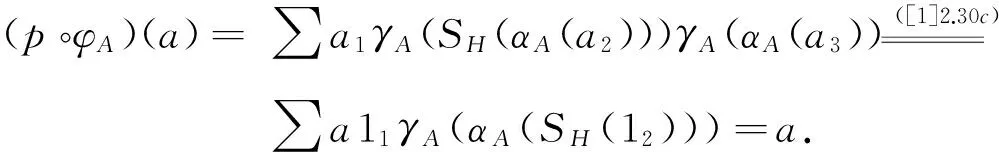
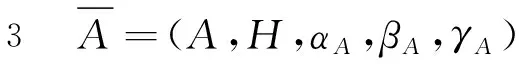
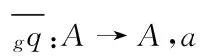
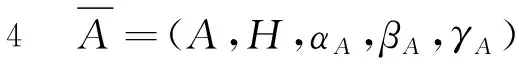
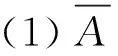
(2)μA°(βi⊗iα)=μA°τA,A°(βi⊗iα).

证明 (1)⟹(2)的证明.因为m是代数同态，所以有m°μA⊗HA((1⊗a)⊗(b⊗1))=μA°(m⊗m)((1⊗a)⊗(b⊗1)).方便起见，将iA,A(a⊗Hb)记为∑a*⊗b*，进一步有，

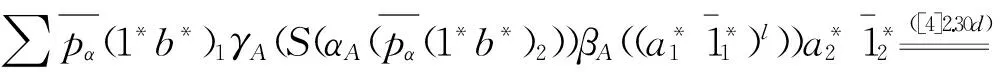
μA°(m⊗m)((1⊗a)⊗(b⊗1))=

故

μA°(βi⊗iα)=μA°τA,A°(βi⊗iα).

(2)⟹(1)的证明.首先证明m是代数同态.事实上，对任意a,b,x,y∈A,有

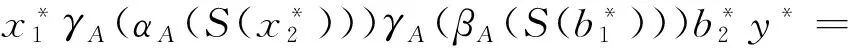
μA°(m⊗m)((a⊗Hb)⊗(x⊗Hy));

m°ηA⊗HA=

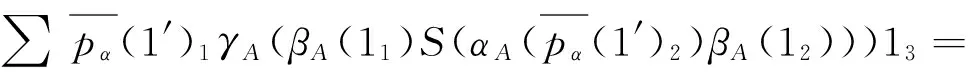
∑11γA(S(αA(12)))=γA(1)=1.

αA°m(a⊗Hb)=

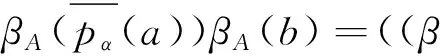
∑γA(h1)γA(S(αA(γA(h2))))γA(h3)=

∑γA(h1)γA(S(h2))γA(h3)=γA(h).

再者，必须证明m°SA⊗HA=S°m.事实上，对任意a,b∈A和h∈H，有

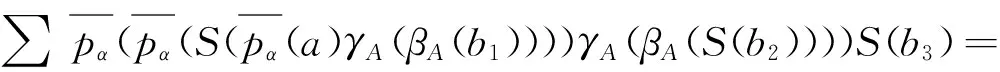
γA(S(βA(S(b2)1)))S(b2)2=

∑S(γA(βA(b1)))γA(S(βA(S(b2)1)))S(b2)2×

∑a1γA(S(αA(a2))βA(b1))γA(S(βA(b1)))b3=

因而有

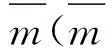
∑a1γA(S(αA(a4)))b1γA(S(αA(b2)))×

γA(S(αA(a2γA(αA(a3)))))c=∑a1γA(S(αA(a3)))b1γA(S(αA(b2)))γA(S(αA(a2))l)c=

∑a1γA(S(αA(a2)))b1γA(S(αA(b2)))c=

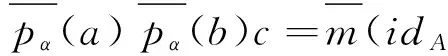
定理4证毕.

[1]LODAYLJ.Spaceswithfinitelymanynontrivialhomotopygroups[J]. J Pure Appl Algebra,1982,24(2):179-202.

[4] BOHM G, NILL F, SZLACHANYI K. Weak Hopf Algebras (I): Integral theory andC*-structure[J].Journal of Algebra,1999,221(2):385-438.

[5] BESPALOV Y. Crossed modules and quantum groups in Braided Categories[J]. Appl Categ Structure,1997,5(2):155-204.

CHEN Xiaoyuan

(ZhejiangBusinessCollege,Hangzhou310053,China)

In this paper, we first introduce the notions of pre-cat weak Hopf algebras and cat weak Hopf algebras to characterize the structures of weak Hopf algebras with projections. Then, we give the monoidal category of these objects which generalize the results of cat Hopf algebras and cat-groups introduced by LODAY.

weak Hopf algebra; projection; cat weak Hopf algebra

2015-01-21.

陈笑缘(1963-)，ORCID:http://orcid.org/0000-0003-2898-9976,女，教授，主要从事代数学研究,E-mail:cxy5988@sina.com.

10.3785/j.issn.1008-9497.2017.02.010

O 153.3

A

1008-9497(2017)02-181-05

Cat weak Hopf algebras. Journal of Zhejiang University(Science Edition), 2017,44(2):181-185