单位圆到任意多边形区域的Schwarz Christoffel变换数值解法
崔建斌,姬安召,王玉风,于江涛,周华龙
(1.陇东学院 数学与统计学院,甘肃 庆阳 745000; 2.陇东学院 能源工程学院,甘肃 庆阳 745000)
单位圆到任意多边形区域的Schwarz Christoffel变换数值解法
崔建斌1,姬安召2,王玉风2,于江涛2,周华龙2
(1.陇东学院 数学与统计学院,甘肃 庆阳 745000; 2.陇东学院 能源工程学院,甘肃 庆阳 745000)
Schwarz Christoffel变换技术在处理某些工程问题时具有重要作用. 从黎曼存在定理出发,建立了单位圆到任意多边形区域的映射函数Schwarz Christoffel变换模型,采用LevenbergMarquardt算法求解含约束条件的非线性映射函数Schwarz Christoffel变换模型参数系统.针对映射函数中出现的奇异积分问题,对映射函数进行2次参数变换,将其化为高斯雅克比型积分,以积分路径中的奇异点为界,缩短积分路径,对子路径采用修正高斯积分方法进行计算.通过指数变换、连乘变换和累加变换,使任意初值问题均可进行迭代计算并满足初值的约束条件.提出以边长绝对误差和顶点绝对误差为迭代计算的收敛条件,并保证了映射函数的精度.给出了11顶点多边形区域映射函数的求解算例,4种方案的计算结果表明,Schwarz Christoffel变换数值解法操作简单、精度高、收敛快.
修正高斯雅克比型积分;单位圆;初值变换;LevenbergMarquardt算法;Schwarz Christoffel变换
0 引 言
Schwarz Christoffel变换(以下简称SC变换)模型在解决实际工程问题时具有重要作用.SC变换能将二维空间上边界复杂的几何体映射到另一个二维空间的形状简单的几何体上,从而简化对复杂边界工程问题的处理.SC变换在油气地下渗流力学、岩土力学、流体力学和电磁学等研究领域有着广泛的应用.目前,国内已有一些关于SC变换数值计算方法的研究成果,王刚等[12]采用牛顿拉夫森迭代法导出了从多角形区域到上半平面映射和槽型区域映射的SC变换求解方法,但未涉及多角形区域到单位圆的计算.祝江鸿等[34]采用SC洛朗级数模型导出了地下开挖隧道断面到单位圆映射的计算方法,但对于复杂开挖断面,因级数构成项较多而求解复杂.文献[57]均以SC级数模型建立多角形区域到单位圆映射计算,其级数模型构成复杂、计算量大,精度难以控制.文献[8]研究了多角形区域到单位圆的映射,但由于奇异积分计算精度较低,要得到高精度的结果则比较困难.文献[9]研究了多角形区域到上半平面SC逆变换的计算方法,同样,计算结果精确但耗时较长.文献[10]主要探讨了由多角形区域到上半平面SC变换的数值解法.笔者借鉴前人的研究成果,通过研究多角形区域到单位圆映射SC变换模型,经2次参数变换,将沿单位圆复积分转换为实积分,并建立了其与高斯雅克比型积分的关系,提出可通过搜寻奇异点缩短积分路径,并在子路径中采用修正高斯雅克比积分.采用上述方法解决了计算过程中出现的奇异积分问题,亦提高了积分精度.结合LevenbergMarquardt最优化算法求解非线性积分方程组,寻求由单位圆到多角形区域SC变换的精确高效的数值解法.

图1 单位圆映射到任意多角形区域变换示意图Fig.1 Transformation diagram of unit circleto the polygonal region
1 基本模型
在复平面W上有N(N≥3)边形,其顶点和内角分别为Wj和παj(j=1,2,…,N).将单位圆上的点映射在W平面上的SC变换公式为
(1)
其中,K为伸缩系数,C为变换中心,παj为W平面多角形内角,zj为单位圆上的点.
但在实际工程问题研究中,一般多角形区域是已知的,需求解与多边形顶点对应的单位圆上的映射点.据黎曼原理,要确定式(1),则参数zj(j=1,2,…,N)中有3个点必须选定.不妨假定zN-2=-1+0i,zN-1=0-1i,zN=1+0i,亦可根据实际工程问题选择其他点.在上述假定条件下,式(1)中zj(j=1,2,…,N)满足:
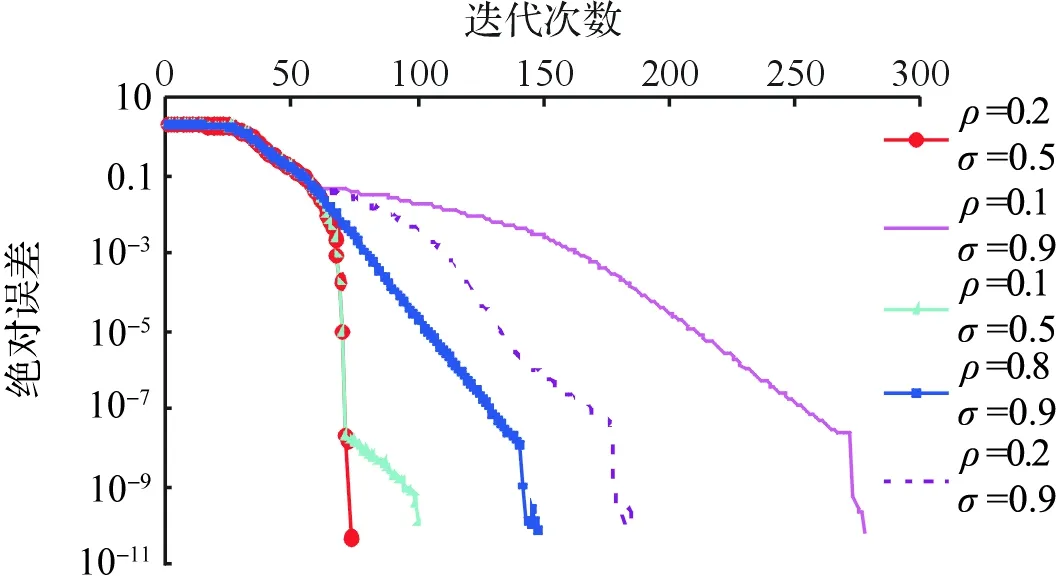
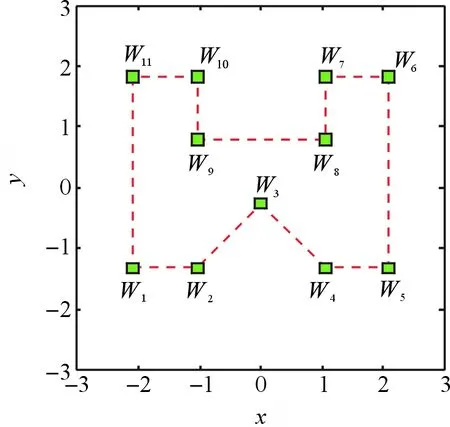
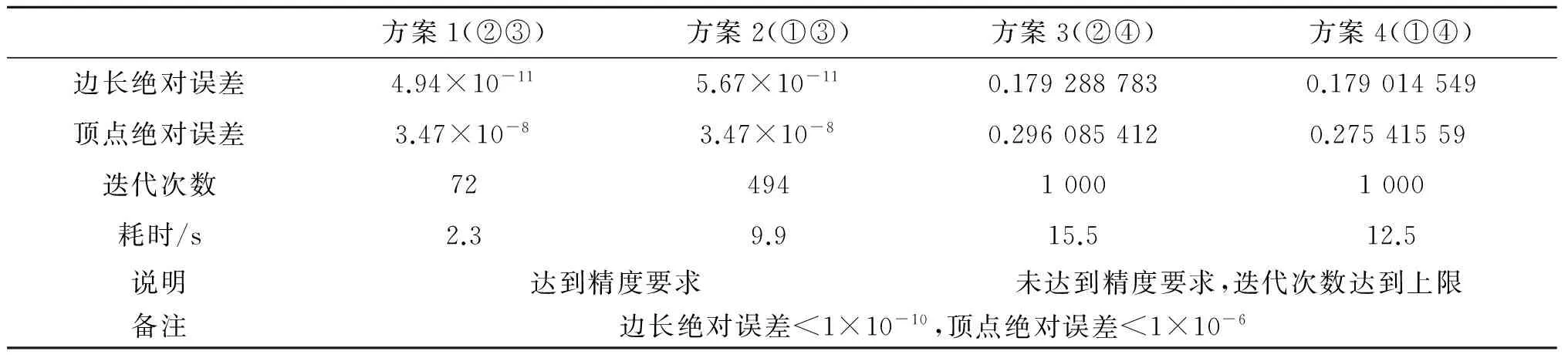
0 (2) 由式(1)可得多边形顶点Wi(i=1,2,…,N)为 (3) 由式(3)则有 (4) 用相邻两点之间的边长比值可消去伸缩系数,从而减少未知量的求解,由式(4)可得 (5) 令 (6) 则式(5)可表示为 (7) (8) 通过求解非线性系统积分方程组式(8),可得未知参数zj(j=1,2,…,N-3). 由式(4)可求得伸缩系数K: (9) 由式(3),结合未知参数zj(j=1,2,…,N-3)与伸缩系数K的求解值,可得变换中心C: (10) 2.1 高斯雅克比型积分 根据以上分析,为了求解SC变换参数问题式(8)~(10),必须计算式(6)的积分.分析实际问题可知,式(6)积分路径在单位圆的圆弧上,积分的起点zi和终点zi+1为奇点.为了求解式(6)的奇异积分,对其作1次参数变换,因zi在单位圆上,令zi=eiθi,其中θi为复数zi的辐角主值,代入式(6)可得 (11) 为了计算式(11)的奇异积分,对式(11)进行2次参数变换: 令 (12) 令 (13) 其中,当j=i时,该项的模可近似表示为 则式(11)可表示为 (14) 式(14)即为高斯雅克比型积分,但需注意其积分的起点和终点都存在奇异点,这里只给出了积分起点奇异点的处理方法,为了处理积分终点的奇异点,只需将积分区间划分为若干个子路径,因子路径内不含奇异点.具体划分方法参见2.2节积分路径奇异点的确定.根据文献[11],式(14)可表示为: (15) (16) 第2步 寻找子区间的奇异值,由式(16)可得奇异值的条件为 (j=1,2,…,start-1,start,…,N-1;start=i). 第5步 若dist≥1,采用校正后的零点和权值进行积分. 2.3 校正高斯雅克比型积分零点与权值 结合式(12)与(14),校正后的零点为 (17) 考虑高斯雅克比型积分式(14),校正后的权值 (18) 对非线性系统式(8)的求解,还得考虑其约束条件0 由式(8)与式(2),得到约束条件下的非线性系统求解问题: (19) 3.1 约束条件的变换 在采用迭代法求解式(19)的过程中,未知量zj(j=1,2,…,N-3)在迭代过程中有可能出现不满足式(2)的情况,为此对约束条件做适当的变换[1415],使其在求解过程中始终满足约束条件.变换过程如下: 第5步 计算迭代值向量Y=[y1,y2,…,yN3]T,yj=eiθj. 通过上述变化后,只要给定任意初值向量X0,迭代值向量Y必然满足式(2). 3.2LevenbergMarquardt算法[16]的参数优化及数值计算方案 图2 LevenbergMarquardt算法中参数、迭代次数与误差关系曲线Fig.2 The relationship curves of number of iterations,error and parameters in LevenbergMarquardt algorithm 在采用LevenbergMarquardt算法求解式(19)时,由ρ与σ取值与迭代次数、误差的关系曲线(见图(2))可以看出,在迭代初期,ρ和σ的取值对绝对误差的影响较小,收敛速度较慢,当迭代次数大于60时,ρ和σ的取值对绝对误差的影响较大,收敛速度差异较大.通过反复迭代计算,得到当ρ=0.2,σ=0.5时,收敛速度最快,为此推荐使用ρ=0.2,σ=0.5. 表1 非线性积分方程组数值计算方案Table 1 Numerical scheme for nonlinear integral equations 通过上述分析,求解非线性积分方程组式(19),初值必须满足式(2),对初值的处理主要采用上述约束条件的变换方法:包含连乘变换和无连乘变换,所以对初值处理有2种选择方案.对于出现的奇异积分,可直接采用式(14)修正高斯雅克比积分或式(16)子路径修正高斯雅克比积分进行计算.这样共有4种计算方案,其计算结果见表3. i=1,2,…,N-2, (20) i=1,2,…,N-2. (21) 平面封闭区域多边形如图3所示,这里共有11个顶点封闭多边形.表2是SC变换参数的计算结果,由于篇幅限制,仅列出②③、①③和②④3种计算方案的结果.从表2可以看出,前2种方案的计算结果很接近,说明初值变换选择的2种方案均可行,但奇异积分处理方法的选择对结果影响很大. 图3 多边形平面图Fig.3 Polygon plane graph 方案1(②③)方案2(①③)方案3(②④)z1-0.9730436674+i*0.2306209473-0.9730436674+i*0.2306209474-0.989757743+i*0.142757174z2-0.9759654834+i*0.2179251598-0.9759654834+i*0.2179251599-0.990369302+i*0.138450875z3-0.9849015986+i*0.1731151093-0.9849015986+i*0.1731151093-0.992766049+i*0.120064866z4-0.9857537888+i*0.1681947321-0.9857537888+i*0.1681947321-0.993105233+i*0.117226258z5-0.9857746537+i*0.1680724015-0.9857746537+i*0.1680724015-0.99311812+i*0.117117035z6-0.9858563977+i*0.1675922523-0.9858563977+i*0.1675922523-0.993169998+i*0.116676285z7-0.9858588436+i*0.1675778641-0.9858588436+i*0.1675778641-0.99317136+i*0.116664692z8-0.9858878094+i*0.1674073695-0.9858878094+i*0.1674073695-0.993184249+i*0.11655491k-0.29320062207+i*0.48877316531-0.29320062211+i*0.48877316531-0.23382918823+i*0.43935654317c-1.5840515459+i*1.4956209022-1.5840515460+i*1.4956209021-1.6837743041+i*1.6952215685 表3 从单位圆到任意多边形SC变换4种计算方案结果的对比Table 3 Comparison of four calculation schemes for SC transformation from unit circle to arbitrary polygon 通过Matlab软件编写SC变换程序,在PC机上进行计算,由表3可知,若直接采用修正高斯雅克比积分方法,无论如何选择初值变换方案,边长和顶点都不能达到精度要求(即方案3和4),而且计算时间长.方案2与方案1相比,若初值不采用连乘变换,上述变换结果同样满足式(2),但需要多次迭代边长和顶点才能达到精度要求,所以初值的连乘变换能够提高计算速度,故推荐方案1. 5.1 单位圆到多边形区域共形映射函数SC变换模型求解的难点,在于计算过程中出现的奇异积分方程的处理和初值必须满足一定的约束条件.从常规高斯雅克比型积分出发,对SC变换模型进行2次参数变换,通过变换积分方程的形式,以积分路径中的奇异点为界,缩短积分路径,在子路径中采用修正高斯积分方法可有效克服奇异积分计算的困难.对于初值的约束条件,通过指数变换、连乘变换和累加变换巧妙处理迭代值,使其对任意初值均可进行迭代并满足初值的约束条件. 5.2 通过对4种方案的计算分析知,初值和积分方式的选择决定了SC变换模型系数迭代计算的快速性和有效性,提出的子路径修正高斯雅克比积分和初值变换方法可有效解决该问题;以边长的绝对误差和顶点绝对误差作为迭代计算的收敛条件,保证了计算映射函数的映射精度. 5.3 在求解SC变换模型时,初值的连乘变换能够较大幅度减少非线性系统求解过程中的迭代次数. 5.4 LevenbergMarquardt算法对映射函数SC变换模型非线性系统是可行的,当参数ρ与σ取值适当时,LevenbergMarquardt算法收敛较快. 5.5 11个顶点多边形映射函数的求解算例表明,本文给出的从单位圆到多边形区域共形映射函数SC变换模型求解算法具有一定的可操作性. [1] 王刚,许汉珍,顾王明,等.数值许瓦尔兹克力斯托夫变换与数值高斯雅可比型积分[J].海军工程学院学报,1994,1(2):2534. WANG G,XU H Z,GU W M,et al. Numerical schwarzchristoffel transformation and numerical gaussjacobi quadrature[J]. Journal of Naval Academy of Engineering,1994,1(2):2534. [2] 王刚,陆小刚,顾王明.槽形内域中的数值许瓦尔兹克力斯托夫保角变换[J].海军工程学院学报,1995,1(4):1623. WANG G,LU X G,GU W M. Numerical schwarzchristoffel conformal mapping in channel region[J].Journal of Naval Academy of Engineering,1995,1(4):1623. [3] 祝江鸿.隧洞围岩应力复变函数分析法中的解析函数求解[J].应用数学和力学,2013,34(4):345354. ZHU J H. Analytic functions in stress analysis of the surrounding rock for caverns with the complex variable theory[J]. Applied Mathematics and Mechanics,2013,34(4):345354. [4] 祝江鸿,杨建辉,施高萍,等.单位圆外域到任意开挖断面隧洞外域共形映射的计算方法[J].岩土力学,2014,35(1):175183. ZHU J H,YANG J H,SHI G P,et al. Calculating method for conformal mapping from exterior of unit circle to exterior of cavern with arbitrary excavation crosssection[J]. Rock and Soil Mechanics,2014,35(1):175183. [5] 皇甫鹏鹏,伍法权,郭松峰.基于边界点搜索的洞室外域映射函数求解法[J].岩石力学,2011,32(5):14181424. HUANGFU P P,WU F Q,GUO S F. A new method for calculating mapping function of external area of cavern with arbitrary shape based on searching points on boundary[J]. Rock and Soil Mechanics,2011,32(5):14181424. [6] 朱大勇,钱七虎,周早生.复杂形状洞室映射函数的新解法[J].岩石力学与工程学报,1999,18(3):279282. ZHU D Y,QIAN Q H,ZHOU Z S. New method for calculating mapping function of opening with complex shape[J]. Chinese Journal of Rock Mechanics and Engineering,1999,18(3):279282. [7] 王润富.一种保角映射法及其微机实现[J].河海大学学报,1991,19(1):8689. WANG R F. A method of conformal mapping and its computer implementation[J]. Journal of Hohai University,1991,19(1):8689. [8] HU C H. A software package for computing schwarzchristoffel conformal transformation for doubly connected polygonal regions[J]. ACM Transactions on Mathematical Software,1998,24(3):317333. [9] COSTAMAGNA E. Numerical inversion of the schwarzchristoffel conformal transformation: Stripline case studies[J]. Microwave and Optical Technology Letters,2001,28(3):179183. [10] 崔建斌,姬安召,鲁洪江,等.Schwarz Christoffel变换数值解法[J].山东大学学报:理学版,2016,51(4):104111. CUI J B,JI A Z,LU H J,et al. Numerical solution of Schwarz Christoffel transform[J]. Journal of Shandong University: Natural Science,2015,50(12):104111. [11] COSTAMAGNA E. A new approach to standard schwarzchristoffel formula calculations[J]. Microwave and Optical Technology Letters,2002,32(3):196199. [12] DRISCOLL T A. Improvements to the schwarzchristoffel toolbox for matlab[J]. ACM Transactions on Mathematical Software,2005,31(2):239251. [13] HOUGH D M. Asymptotic gauss jacobi quadrature error estimation for schwarzchristoffel integrals[J]. Journal of Approximation Theory,2007,146(2):157173. [14] NATARAJAN S, BORDAS S P A, MAHAPATRA R D. Numerical integration over arbitrary polygonal domains based on schwarzchristoffel conformal mapping[J]. International Journal for Numerical Methods in Engineering,2009,80(1):103134. [15] CROWDY D. The schwarzchristoffel mapping to bounded multiply connected polygonal domains[J]. Proceedings of the Royal Society,2005,146(2061):26532678. [16] 刘浩.大规模非线性方程组和无约束优化方法研究[D].南京:南京航空航天大学,2008. LIU H. Research on Methods for Largescale Nonlinear Equations and Unconstrained Optimization[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,2008. CUI Jianbin1,JI Anzhao2,WANG Yufeng2, YU Jiangtao2, ZHOU Hualong2 (1.MathematicsandStatisticsInstitute,LongdongUniversity,Qingyang745000,GusuProvince,China;2.EnergyEngineeringInstitute,LongdongUniversity,Qingyang745000,GusuProvince,China) Schwarz Christoffel transformation technique has an important role in dealing with engineering problem. Based on the Riemann’s existence theorem, a transform model of Schwarz Christoffel from unit circle to arbitrary polygon area was established. LevenbergMarquardt algorithm was used to solve parameters of the nonlinear mapping function of Schwarz Christoffel with constraint conditions. As to the mapping function in the singular integral problem, the mapping function was twice transformed to Gauss Jacobi integral, then the singular point in the integral path was taken as the boundary; The length of integral path was narrowed, and the modified Gaussian integral was used to calculate the sub path. By the exponential transform, multiplicative transform and accumulation transform process, the arbitrary initial value could be iteratively calculated and the results satisfied the constraints of the initial value. The convergence conditions of the iterative copulation based on the absolute errors of length and absolute error of vertex were put forward to ensure the precision of the mapping function. The solution of the mapping function with 11 vertex polygon region was calculated by four calculation schemes. Results of the four schemes showed that the numerical solution of Schwarz Christoffel transform is simple with high precision and fast convergence. modified Gauss Jacobi type integral; unit circle; initial value transformation; LevenbergMarquardt algorithm; Schwarz Christoffel transformation 20160301. 甘肃省科技计划资助项目(1606RJZM092,1606RJYM259,1506RJYM324). 崔建斌(1972-),ORCID:http://orcid.org/0000000266933415,男,硕士,副教授,主要从事数值分析与数据挖掘研究,Email:cuijb0658@163.com. 10.3785/j.issn.10089497.2017.02.007 O 241 A 1008-9497(2017)02-161-07 Numerical solution method for Schwarz Christoffel transformation from unit circle to arbitrary polygon area. Journal of Zhejiang University(Science Edition), 2017,44(2):161167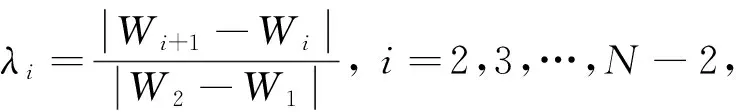
2 Schwarz Christoffel积分



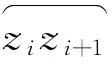

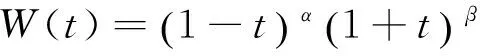
3 非线性系统求解


4 精度评定与算例分析



5 结 论


