杭州城西河网清淤优化调度

杨恩尚，孙志林，倪晓静

(浙江大学 港口海岸与近海工程研究所， 浙江 杭州 310058)

杭州城西河网清淤优化调度

杨恩尚，孙志林*，倪晓静

(浙江大学 港口海岸与近海工程研究所， 浙江 杭州 310058)

引水进入城市河网可快速提升河道水质，但也会导致泥沙淤积等问题；城市河网不仅河道众多，还有水闸等水工建筑物，使得水沙输移问题变得更为复杂.为了使泥沙尽量少淤积于不易清淤的河道，需优化河网水闸的调度.首先建立了考虑水闸的河网一维泥沙输移数学模型，利用实测水沙数据验证其精度.通过模型计算不同引水流量工况下杭州城西河网泥沙的淤积量及淤积分布，得到泥沙淤积率最低以及最利于清淤时的河网水闸优化调度方案，可为城市河网泥沙减淤及清淤提供理论依据和参考.

城市河网；水闸；优化调度；清淤

0 引 言

随着社会经济的发展和生活水平的提高，人们对水环境质量的要求也越来越高[1]，引水进入城市河网可快速有效地改善河道水质[2-4].然而，引水也会带来泥沙淤积问题[5].河网水沙输移及淤积研究，以一维数学模型为主[6].GAMVROUDIS等[7]研究了大尺度河网水沙输移问题，周晨霓等[8]则给出了河网提取集水面积的方法.GOURGUE等[9]较为详细地研究了河口地区河网的水沙输移问题，韩冬等[10]针对河网断流问题提出了一种合理的解决方法.此外，河网模型的水动力[11-12]、数值解析方法[13]均有较为细致的研究.FANG等[14]较为系统地研究了河网沿程泥沙浓度、汊点离散、淤积计算等河网水沙输移问题，通过实测资料验证了该模型的精度，为工程应用提供了理论依据.

近年来，杭州对绕城以内河道配水极为重视，建设了西湖、三堡引水工程，中河双向泵房及钱塘江引水入城工程等.钱塘江引水入城工程为杭州市重点工程，同时也是一项生态建设工程.该工程当前配水的范围主要包括“四河四港”——余杭塘河、沿山河、冯家河、益乐河，紫金港、莲花港、蒋村港、五常港(见图1).工程引水线路总长约12 km，设计引水量为25 m3·s-1，自东穆坞溪引入城西河网，并由余杭塘河流入京杭大运河.由于钱塘江水体含沙量较多，引水必然会引起下游河道及河网的泥沙淤积.因此，研究河网水沙输移及淤积规律，对指导河道清淤的长效管理工作极为必要.

图1 杭州城西河网Fig.1 River network of West Hangzhou

本文通过所建立的河网一维泥沙输移模型，研究杭州城西河网的水动力和泥沙输移及淤积分布规律，预测泥沙淤积发展趋势.计算分析水闸调控配水方案，提出引配水调度建议，以此调控河网泥沙淤积量及其分布，方便清淤，从而降低清淤长效运行的成本，打造流畅、水清的河道水环境，塑造城市景观新形象.

1 数学模型

1.1 基本方程

水流连续方程为

(1)

水流动量方程

(2)

非均匀沙含沙浓度沿程变化为[5]

(3)

河床变形方程

(4)

其中:A为过水面积，Q为流量，R为水力半径，Z为水位，q为第i条支流侧向出(入)流，n为曼宁系数，ζ为动量分配系数，t为时间，x为距离，S*为挟沙能力，S为含沙浓度，B为河宽，α为恢复饱和系数，g为重力加速度，P0k为第k粒级泥沙颗粒所占百分数，N为泥沙级配总数；上标：0为初始时刻，Δt为时间步长，下标Δx为空间步长.

1.2 公式参数

非均匀沙水流挟沙能力公式为[5]

(5)

平均沉速为[5]

(6)

恢复饱和系数为[14]

(7)

上式中下标b代表底部河床.

非平衡调整长度为[14]

Ls=0.73B,

(8)

闸门过流流量计算公式为[15]

(9)

上式中μ为流量系数，b为闸门净宽，a为闸门开启高度，ε为垂向收缩系数.

2 模型验证

2.1 水动力

河网一维数学模型的计算范围为杭州城西河网区域(见图1)，不包含余杭塘河与五常港汊点以西以及沿山河和分流河汊点以西河段，计算断面间隔为50m.河网水流、泥沙以及汊点分流、分沙的求解参照方红卫等[15]的计算方法.上游水边界为东穆坞溪出水口，下游为余杭塘河与冯家河汊点.沿山河、余杭塘河验证点位分别位于沿山河与蒋村港汊点、余杭塘河与冯家河汊点处.

图2 水位计算与实测值比较(2012年8月10日)Fig.2 Comparison of the calculated and measured water level(August 10th, 2012)

模型水动力验证情况如图2所示.从图中不难看出，河网上游的沿山河与下游的余杭塘河计算值与实测值均符合良好，下游的余杭塘河略差，计算误差均在10cm以内，相对误差小于5%.

2.2 泥沙验证

杭州城西河网验证点泥沙级配如图3所示，含沙量计算值与实测值如图4所示.亦不难看出，河网上下游的沿山河和余杭塘河计算精度均较高，上游的沿山河要略优于下游的余杭塘河.这与河网上游河道较少下游汊点较多导致水动力及泥沙条件复杂有关.总体来说，本文所建立的河网水动力及泥沙输移模型精度较高，可进行工程应用.

图3 杭州城西河网泥沙级配Fig.3 Sediment gradation for river network of west Hangzhou

图4 含沙量计算值与实测值比较(2012年8月10日)Fig.4 Comparison of the calculated and measured sediment concentrations (August 10th, 2012)

3 河网优化调度

3.1 调度工况

钱塘江引水入城工程的设计流量为25m3·s-1，实际运行中在钱塘江水体浊度偏大、水位偏低的情况下，为满足防汛要求，需要适当降低引水流量.2010年8月至2011年7月年平均引水流量为11.16m3·s-1，只有设计流量的45%，平均淤积率为81.4%.为减少淤积，即让泥沙尽量淤积在较为宽阔易于清淤的地方，如沿山河与五常港的分岔口附近，需要进一步分析不同引水流量、不同配水工况下的泥沙淤积情况，以期提出优化方案，改进调度方法.考虑10，15，20，25m3·s-1引水流量，并取平均含沙浓度82g·m-3，不同工况下计算五常港、蒋村港、紫金港、莲花港、冯家河等水闸河网的淤积量，分析其淤积规律.

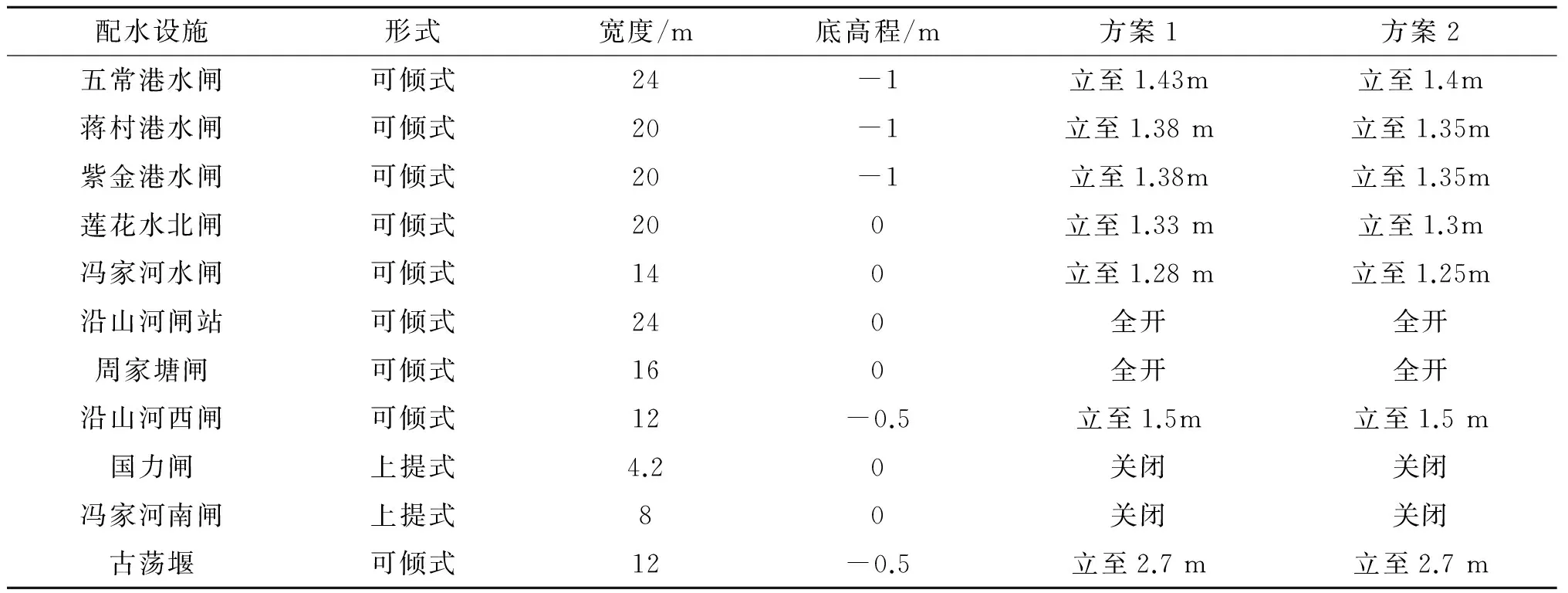
表1 闸站运行方案Table 1 Operation scheme of sluice station

主要船闸、闸门的基本情况如表1所示，其中以调节五常港、蒋村港、紫金港、莲花港、冯家河水闸为主，每个水闸初步确定2个方案.沿山河西闸、国力闸、冯家河南闸、古荡堰2个方案相同，这样共有25即32种组合，结合上面4种不同的引水流量就有128种情况.鉴于数量较多，选取引水流量为10 m3·s-1，对32种工况组合进行研究，根据结果分析淤积规律，以减少工作量并保证结论的可靠性.32种工况如表2所示.

3.2 各工况淤积计算

利用本文建立的河网水沙输移模型，参数中初始含沙浓度取平均值即0.082 kg·m-3，流量为10 m3·s-1，中值粒径d50为7.65 μm，分组粒径分别为2，8，20 μm，各区间所占百分比分别为21%，35%，28%，16%.虽然引水流量固定为10 m3·s-1，但计算得到每条河流的水位、流量并不恒定，且波动较大，体现了河网水流的复杂性，但其均值较为稳定.各工况下流量的变化并不大，闸门提升后该河道的流量会减小0.08～0.18 m3·s-1，其中五常港和沿山河流量变化最大，为0.18 m3·s-1，益乐河、冯家河最小为0.08 m3·s-1.

不同工况组合下的淤积量见图5.其中，淤积率最大为86.8%，为标号25的组合，即五常港、蒋村港、紫金港、莲花港、冯家河闸门分别立至1.4, 1.35, 1.38，1.38，1.28 m.最小的淤积率为77.7%，标号为7，即5个闸门依次立至1.43，1.38，1.35，1.35，1.28 m.其原因应该是莲花港、紫金港的闸门抬高后更多的水流向五常港、蒋村港(流量分别增加0.12，0.15 m3·s-1)，经余杭塘河流出计算区域，水流路程更长，水力条件变化较大，更易发生淤积.紫金港、莲花港闸门的抬升还令沿山河的流速减低，淤积相应增加，从而整个河网的淤积量增大.

表2 工况汇总Table 2 Summary of all working conditions

注 A、B、C、D、E分别代表五常港、蒋村港、紫金港、莲花港、冯家河水闸，“1”“2”分别代表方案1与方案2.

图5 各方案泥沙淤积量Fig.5 Deposition amount of channel for each working condition

沿山河的淤积率由22.7%增加到26.1%，余杭塘河也淤积了更多的泥沙，淤积率从6.07%提高到10.37%，此2河是整个水系中最长的，且断面形状变化多，易于淤积，淤积率变化也最大.标号为10的工况淤积率为81%，其数值虽不是最大，但较其他工况而言，五常港与沿山河汊口50 m范围内淤积厚度最大，为15.8 cm，标号7，25的工况组合下该

位置的淤积厚度分别为12.4，13.3 cm.五常港与沿山河汊口也是各工况下河网淤积最厚的区域.标号10的工况为五常港、蒋村港、紫金港、莲花港、冯家河的闸门分别立至1.43，1.35，1.38，1.38，1.25 m.这个组合使得五常港内水流流速降低，沿山河水流加快，流速在汊点附近波动大，产生了更多淤积.

值得注意的是，并不是某河段闸门提升，其淤积量一定会增加，因为该河段流量的变化还受其他河道闸门升降的影响，需要综合整个河网来考虑.河网的淤积是一个动态的且相互影响相互作用的过程，影响河道淤积的因素很多，需要综合分析.进一步考虑7，10，25的工况组合，考虑其在流量分别为10，15，20，25 m3·s-1时的淤积情况，以进一步分析河网淤积分布，探寻淤积规律.

3.3 不同流量下各工况淤积计算

初始流量分别为15，20，25 m3·s-1，河网水动力及泥沙输移计算值如图6所示.河网的水力要素如流量、水深、流速波动较大，波动周期与波动幅度都不稳定，规律性并不强，随着流量的增大，波动更为剧烈，但各河道的流量均值较为稳定.虽然流量从10 m3·s-1增加到25 m3·s-1，但各河道的流量占总流量的比值仍较为稳定.沿山河、五常港、蒋村港、紫金港与莲花港的流量占总引水流量的比值依次为85%，15%，24%，35%，26%.莲花港流向益乐河的流量约占其总流量的42%，因为冯家河南闸封闭，所以益乐河与冯家河流量平均值相同(同时刻并不相同).

随着流量的增加，淤积率有效降低.25 m3·s-1流量情况下各工况组合相较10 m3·s-1时淤积率降低约10%，减淤作用明显.为减少淤积，应尽量增大引水流量.如果引水流量不能增大，或者增大引水流量比较困难，通过调整工况组合也能有效减少淤积.其中在10，15，20，25 m3·s-1引水流量下，工况7相较工况25其淤积率分别降低9.1%，8.5%，8.1%，7.8%，降低的淤积率数值虽然没有增加的流量那么大，但效果也较明显.

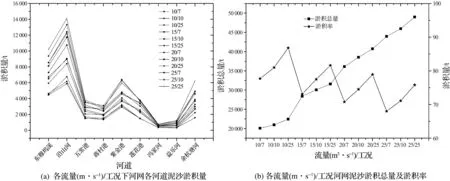
图6 各流量/工况下泥沙淤积量Fig.6 Deposition amount of channels for each discharge and working condition

东穆坞溪的淤积率随着流量的增大而降低，即更多的泥沙淤积在了下游河段，所以增加流量可有效减少东穆坞溪的淤积.除了最长的河流沿山河与余杭塘河外，其他河段淤积率变化较小.冯家河、益乐河的淤积量很小，变化也不大.

值得注意的是，随着流量的增加，淤积率虽有降低，但总的淤积量以及淤积厚度却有较明显的增加.平均来看，除东穆坞溪外，大部分河段的淤积量接近5 cm，局部淤积厚度较大，其中沿山河与五常港交叉口50 m范围内的淤积厚度最大.引水流量为25 m3·s-1、标号10的工况下该处淤积厚度为29.6 cm，是最大的计算值.河网清淤时，应重点考虑该区域.

图7 各流量/工况下沿山河、五常港汊口淤积量及厚度Fig.7 Deposition amount and depth for the inlet of Yanshan and Wuchang channels in each discharge and working condition

各流量/工况下，沿山河、五常港汊口淤积量及厚度如图7所示.不难看出，沿山河与五常港汊口50 m范围内的平均淤积厚度随着流量的增大而增加，工况组合10较工况组合7和25的淤积厚度大2～10 cm，流量越大时该值也越大.相应该河段泥沙淤积量要多18%以上.由于该处交通便利，易于工程机械作业，可显著降低清淤费用.

4 结 论

引水入城市河网在快速改善河道水质的同时也导致了泥沙淤积.首先，建立了河网一维水动力及泥沙输移模型，并利用实测水沙资料验证模型的精度.针对工程中水闸等水工建筑物的运行方案，提出了32种运行工况.分别分析引水流量为15，20，25 m3·s-1时的河网泥沙淤积情况，结果表明，五常港、蒋村港、紫金港、莲花港、冯家河的闸门依次立至1.43，1.38，1.35，1.35，1.28 m时，河网总体泥沙淤积率最低.上述5个闸门分别立至1.43，1.35，1.38，1.38，1.25 m时，最易于清淤的沿山河与五常港汊口淤积量及淤积厚度最大.河网淤积是一个相互影响、相互作用的动态过程，影响河道淤积的因素很多，需要综合分析.所得结论可为城市河网清淤提供参考，通过优化调度减少河网泥沙淤积量，从而降低清淤费用.

[1] 梁斌，王超，王沛芳.“引江济太”工程背景下河网稀释净污需水计算及其应用[J].河海大学学报：自然科学版，2004，32(1)：32-37. LIANG B, WANG C, WANG P F. Method for calculation of water demand by pollutant dilution and purification in river networks and its application to the Yangtze River-Taihu Lake Water Transfer Project [J]. Journal of Hohai University: Natural Sciences，2004，32(1)：32-37.

[2] 陈振涛，滑磊，金倩楠.引水改善城市河网水质效果评估研究[J].长江科学院院报，2015，32(7)：45-51. CHEN Z T，HUA L，JIN Q N. Assessing the efficacy of water diversion to improve water quality in city river network[J]. Journal of Yangtze River Scientific Research Institute，2015，32(7)：45-51.

[3] 黄发明.钱塘江微污染寡碳引水脱氮示范工程试验研究[D].武汉：武汉理工大学，2012. HUANG F M. Research for Qiantang River Micro-polluted Oligo Carbon Water Nitrogen Demonstration Engineering[D]. Wuhan: Wuhan University of Technology,2012.

[4] 王振宇，李富强，陈昌军.钱塘江引水入城工程水质分析及预测研究[J].水力发电学报，2005，24(4)：47-51. WANG Z Y, LI F Q, CHEN C J. Study on water quality analysis and forecast of Qiantang river diversion project[J]. Journal of Hydroelectric Engineering，2005，24(4)：47-51.

[5] 孙志林，杨恩尚，曾田力，等.考虑侧向出沙的河网非均匀沙输移[J].水利学报，2016，47(1)：72-77. SUN Z L，YANG E S，ZENG T L，et al. Nonuniform sediment transport with lateral output in river networks[J]. Journal of Hydraulic Engineering，2016，47(1)：72-77.

[6] HU J T，LI S Y，GENG B X. Modeling the mass flux budgets of water and suspended sediments for the river network and estuary in the Pearl River Delta，China [J]. Journal of Marine Systems，2011(88)：252-266.

[7] GAMVROUDIS C，NIKOLAIDIS N P，TZORAKI O，et al. Water and sediment transport modeling of a large temporary river basin in Greece [J]. Science of the Total Environment，2015(508)：354-365.

[8] 周晨霓，任德智.基于DEM的西藏鲁朗河流域数字河网提取时集水面积阈值的确定[J].中国农村水利水电，2014(10):49-52. ZHOU C N, REN D Z. Determination of drainage area threshold for extraction of DEM-based digital drainage networks in the Lulang River of Tibet [J]. China Rural Water Conservancy and Hydropower，2014(10):49-52.

[9] GOURGUE O，BAEYENS W，CHEN M S，et al. A depth-averaged two-dimensional sediment transport model for environmental studies in the Scheldt Estuary and tidal river network [J]. Journal of Marine Systems,2013(128)：27-39.

[10] 韩冬，方红卫，陈明洪.一维河网模型断流问题研究[J].水力发电学报，2012，31(2):95-99. HAN D，FANG H W，CHEN M H. Study on zero flow with one-dimensional numerical model of river channel network[J]. Journal of Hydroelectric Engineering，2012，31(2):95-99.

[11] 张大伟，权锦，马建明，等.基于非恒定流模型的山洪沟水面线计算[J].水利水电技术，2016，47(2)：123-127. ZHANG D W，QUAN J，MA J M，et al. Unsteady flow model-based calculation of mountain torrent ditch water level[J]. Water Resources and Hydropower Engineering，2016，47(2)：123-127.

[12] 管仪庆，张丹蓉，陈丕翔，等.闲林水库水动力特性模拟研究[J].水利学报，2007(S1)：293-298. GUAN Y Q, ZHANG D R, CHEN P X, et al. Simulation of hydrodynamic characteristics of xianlin reservoir[J]. Journal of Hydraulic Engineering，2007(S1)：293-298.

[13] 沙玉坤，程根伟，李卫朋，等.基于临界支撑流量的西藏典型河流源头位置确定及河网解析研究[J].四川大学学报:工程科学版，2014，46(6)：49-55. SHA Y K，CHENG G W，LI W P，et al. Determination of a riverhead based on critical support discharge and river network analysis [J]. Journal of Sichuan University: Engineering Science Edition，2014，46(6)：49-55.

[14] FANG H W，CHEN M H，CHEN Q H. One-dimensional numerical simulation of non-uniform sediment transport under unsteady flows[J]. International Journal of Sediment Research，2008(23)：315-328.

[15] 方红卫，何国建，郑邦民.水沙输移数学模型[M].北京：科学出版社，2015. FANG H W, HE G J, ZHENG B M. Mathematical Models for Hydrodynamics and Sediment Transport[M]. Beijing: Science Press,2015.

YANG Enshang, SUN Zhilin，NI Xiaojing

(InstituteofPort,CoastalandOffshoreEngineering,ZhejiangUniversity,Hangzhou310058,China)

Diversion into the urban river networks can quickly improve the water quality, but it brings the problem of sediment deposition at the same time. Urban river networks possess not only numerous channels but also hydraulic structures such as sluices, which makes the research on water flow and sediment transport more complex. In order to deposit more sediment in the river reaches which are easy to be dredged, optimization measures of sluice scheduling are thus necessary. This paper established a 1D mathematical model of sediment transport considering sluices for river networks in the first place. Then, the model was verified by the measured data of water flow and sediment. The amount of sediment deposition and its distribution in west Hangzhou river network were calculated under each operating condition of the sluices with different diversion discharges by the model. Optimal scheduling of the sluices that had the lowest deposition ratio and the most conducive dredging work was further proposed as a result of the analysis on calculation data, respectively. The results this paper presents can provide a useful reference and guidance for sediment dredging of urban river networks.

urban river network; sluice; optimal scheduling; dredging

2016-06-08.

教育部博士点基金资助项目(2120101110108).

杨恩尚(1986-)，ORCID：http://orcid.org/0000-0001-8646-054X，男，博士研究生，主要从事水沙运动力学及数值模拟研究.

*通信作者，ORCID：http://orcid.org/0000-0002-6446-3472，E-mail：oceansun@zju.edu.cn.

10.3785/j.issn.1008-9497.2017.02.012

TV 14

A

1008-9497(2017)02-191-07

Optimal scheduling on dredging for river network of west Hangzhou. Journal of Zhejiang University(Science Edition), 2017,44(2):191-197