一个非单调非齐次核的Hilbert型积分不等式

钟建华，陈 强,曾志红

(1. 广东第二师范学院 数学系， 广东 广州 510303； 2. 广东第二师范学院 计算机科学系， 广东 广州 510303;3. 广东第二师范学院 学报编辑部， 广东 广州 510303)

一个非单调非齐次核的Hilbert型积分不等式

钟建华1，陈 强2*,曾志红3

(1. 广东第二师范学院 数学系， 广东 广州 510303； 2. 广东第二师范学院 计算机科学系， 广东 广州 510303;3. 广东第二师范学院 学报编辑部， 广东 广州 510303)

通过引入参数σ和应用权函数的方法, 建立了一个具有最佳常数因子的非单调且非齐次核的Hilbert型积分不等式及其等价形式, 并考虑了特殊结果.

Hilbert型积分不等式；权系数；参数；等价式; 非齐次核

(1)

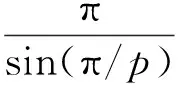
文献[4]引入了2对共轭指数(p,q)与(r,s), 当λ>0,f,g≥0时,有如下-λ齐次核的Hilbert型积分不等式:

(2)

(3)

关于非齐次核的Hilbert型不等式的研究不断推陈出新, 文献[5]得到一个非齐次核的Hilbert型不等式:

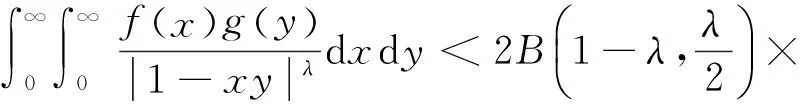
(4)

2012年,文献[6]研究了非齐次核的Hilbert型不等式的一般理论,得到了一个重要的推广:

及

时,有

(5)

本文应用一个非单调双曲正割函数[7]:

(6)

其所确定的非齐次核:

受式(3)～(5)的研究思路启发,在此引入参数σ>0,应用权系数及实分析方法,得到了一个具有最佳常数因子的Hilbert型不等式和等价式, 并考虑了一些特殊结果.

1 引 理

引理1 若σ>0,且h(t)如式(6)所定义,定义如下权系数:

(7)

则ωσ(y)是与y无关的正数, 且

ωσ(y)=k(σ):=Γ(σ)η(σ).

(8)

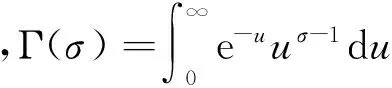
证明 对式(7)做u=xy变换，则有

(9)

将其代入式(9),并令t=(2k+3)u,得

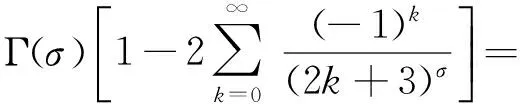
在上式中自然有

则有ωσ(y)=Γ(σ)η(σ).即式(8)成立.证毕.

(10)

k(σ) 的定义见式(8).

证明 配方并由带权的Hölder不等式[8]及式(7), 有

(11)

由式(11)、Fubini定理[9]及式(7)和(8),有

即式(10)成立.证毕.

2 主要结果

时，有如下等价式:

(12)

(13)

其中,k(σ)及kp(σ)均为最佳值.

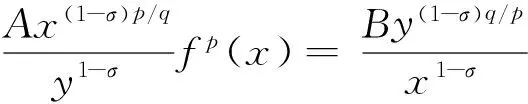
不妨设A≠0(否则,A=B=0), 则有

通过配方，并由Hölder不等式[8],有

(14)

(15)

即

(16)

对式(16)两边p次方,可得式(13),且式(13)与式(12)等价.

则可算得

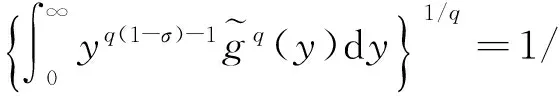
由Fubini定理[9],并对下式中的内积分做u=xy变换,可得

(17)

运用Fatou引理[9]及式(17),有

这与假设矛盾,故k=k(σ)必为式(12)的最佳值.式(13)的常数因子kp(σ)必为最佳值,否则,由式(14),必导出式(12)的常数因子非最佳值的矛盾结论.证毕.

(18)

(19)

其中,常数因子

当σ=1时,有

式(12)和(13)变为如下具有最佳常数因子的等价不等式:

(20)

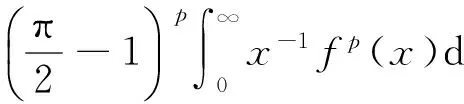
(21)

[1]HARDYGH.NoteonatheoremofHilbertconcerningseriesofpositiveterm[J]. Proceeding of the London Math Society,1925,23(2):45-46.

[2] HARDY G H,LITTLEWOOD J E,POLYE G. Inequalities[M]. Cambridge: Cambridge Univ Press,1952.

[3] MINTRINOVIC D S,PECARIC J E,FINK A M. Inequalities Involving Functions and Their Integrals and Derivatives[M]. Boston: Kluwer Academic Publishers,1991.

[4] YANG B C. On an extension of Hilbert’s inequality with some parameters[J]. The Australian Journal of Mathematical Analysis and Applications,2004,1(1):1-8.

[5] 杨必成.算子范数与Hilbert型不等式[M].北京:科学出版社,2009:300-307. YANG B C. The Norm of Operator and Hilbert-type Inequalities[M]. Beijing: The Science Press,2009:300-307.

[6] 杨必成.关于一个非齐次核的Hilbert型积分算子[J].应用泛函分析学报, 2012,14(1):84-88. YANG B C. On a Hilbert-type integral operator with the none-homogeneous kernels[J]. Acta Analysis Functionalis Applicata ,2012,14(1):84-88.

[7] 钟玉泉.复变函数论[M].北京:高等教育出版社,2003. ZHONG Y Q. Theory of Functions of Complex Variable[M]. Beijing: Higher Education Press,2003.

[8] 匡继昌.常用不等式[M].济南:山东科学技术出版社,2004:4-5. KUANG J C. Applied Inequalities[M]. Jinan: Shandong Science and Technology Press, 2004:4-5.

[9] 匡继昌.实分析引论[M].长沙:湖南教育出版社,1996:45-46. KUANG J C. Real Analysis [M]. Changsha: Hunan Educational Press,1996:45-46.

ZHONG Jianhua1, CHEN Qiang2， ZENG Zhihong3

(1.DepartmentofMathematics,GuangdongUniversityofEducation,Guangzhou510303,China; 2.DepartmentofComputerScience,GuangdongUniversityofEducation,Guangzhou510303,China; 3.EditorialDepartmentofJournal,GuangdongUniversityofEducation,Guangzhou510303,China)

By introducing a parameterσ, a Hilbert-type integral inequality with a non-monotone and non-homogeneous kernel and a best constant factor was established by the way of weight functions. The equivalent forms and some particular cases are also considered.

Hilbert-type integral inequality; weight coefficient; parameter; equivalent form; non-homogeneous kernel

2016-04-01.

国家自然科学基金资助项目(61370186,61640222)；广东省省级科技计划项目(2013A011403002,2014B010116001);广东第二师范学院教授科研专项经费研究项目(2015ARF25).

钟建华(1962-)，ORCID:http://orcid.org/0000-0002-6094-7920,男，副教授，主要从事几何与Hilbert型不等式研究.

*通信作者，ORCID:http://orcid.org/0000-0001-8010-6398,E-mail:cq_c@gdei.edu.cn.

10.3785/j.issn.1008-9497.2017.02.005

O 178

A

1008-9497(2017)02-150-04

A Hilbert-type integral inequality with a non-monotone and non-homogeneous kernel. Journal of Zhejiang University(Science Edition), 2017,44(2):150-153