高考题引发的对函数f(x)=sin(ωx+φ)性质思考

广东省佛山市实验中学(528061) 谢伟帆

高考题引发的对函数f(x)=sin(ωx+φ)性质思考

广东省佛山市实验中学(528061) 谢伟帆

A.11B.9C.7D.5

这道题目作为选择题最后一题,综合考察了f(x)= sin(ωx+φ)的零点、对称轴及单调性.

做到这里,遇到了问题：对于每一个ω,都有满足题设条件对应的φ吗?如果有,该如何确定φ的值,两个值都能取,还是只能取其中一个?观察③④式发现,只要ω能写成③的形式,就存在对应的k1,k2,通过④式的计算可得出对应的φ,因此φ必存在(此时φ不一定满足接下来可以利用正弦函数T=2π找出φ的等价值,事实上,φ值只能等价于二者之一(后文会解释).

简单来分析,当ω＞0(ω/=1)时,要使f(x)= sin(x+φ)的所有零点也是f(x)=sin(ωx+φ)的零点,后者的周期必须比前者周期短,易知ω＞1,那么ω会是整数吗?笔者先考虑φ=0,得到定理一.

定理一f(x)=sinx零点为f(x)=sin(ωx)零点的充要条件是ω为整数.

证明充分性f(x)=sinx的所有零点为x=kπ(∀k∈Z),则ωx=ωkπ=k1π(k1∈Z),sin(k1π)=0,得证.

必要性 反证法,假设ω不为整数,f(x)=sinx的零点为x=kπ(∀k∈Z),取k=1,x=π,则ωx=ωπ不是π的整数倍,因此sin(ωx)/=0,与f(x)=sinx的零点为f(x)=sin(ωx)的零点矛盾.

根据定理一的提示,考虑φ/=0的情况,得到定理二.

定理二f(x)=sin(x+φ)零点为f(x)=sin(ωx+φ)零点的充要条件是(ω∈Z,m∈Z,n∈Z).

证明充分性f(x)=sin(x+φ)的所有零点为x=-φ+k1π(∀k1∈Z),则

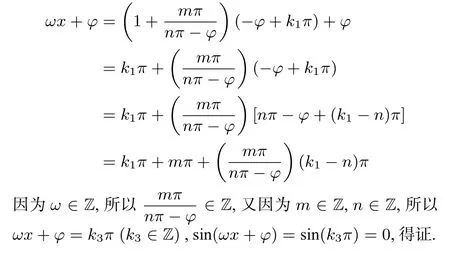
必要性f(x)=sin(x+φ)的所有零点为x=-φ+k1π(∀k1∈Z),因为f(x)=sin(x+φ)的零点为f(x)=sin(ωx+φ)的零点,所以不恒等于0,与f(x)=sin(x+φ)零点为f(x)=sin(ωx+φ)零点矛盾.

这样就解决了开始的问题,找到了使得f(x)= sin(x+φ)的所有零点也是f(x)=sin(ωx+φ)的零点的充要条件.那对称轴有没有类似的结论呢?经过笔者的思考,得到定理三.

那么使得f(x)=sin(x+φ)的所有零点是f(x)= sin(ωx+φ)的对称轴的充要条件以及f(x)=sin(x+φ)的所有对称轴是f(x)=sin(ωx+φ)的零点的充要条件分别又是什么呢?由于证明过程和定理二、三类似,下面的证明过程不再赘述.

定理四f(x)=sin(x+φ)零点为f(x)=sin(ωx+φ)对称轴的充要条件是(ω∈Z,m∈Z,n∈Z).

证明略.

通过研究函数f(x)=sin(ωx+φ)的性质,问题得到解决,但是过程繁杂,那有没有更简单的方法找出φ的取值呢?经过思考,发现中k2-k1与k1+k2的取值是有关联的,由数论的知识得

(1)若k2-k1是奇数,则k2,k1为一奇一偶,所以k1+k2必为奇数,这样也能解释φ值只能等于-二者之一,此时取

(2)若k2-k1是偶数,则k2,k1同为奇数,或者同为偶数,所以k1+k2必为偶数,此时取

A选项ω=11=1+2×5,k2-k1=5,对应同理可知C选项B、D选项对应这样能更快捷地找出φ的值.