初探三种垂直关系相互转化的基本活动经验

湖北省远安县第一高级中学(444200) 王康垣 王艳

初探三种垂直关系相互转化的基本活动经验

湖北省远安县第一高级中学(444200) 王康垣 王艳

1.问题提出在研究空间垂直关系问题中获得的以线面垂直为枢纽的三种垂直关系相互转化的经验.

2.内容界定

空间中的垂直关系是立体几何中重要的位置关系之一,线线垂直或面面垂直都可转化为线面垂直来解决.其关系为：线线垂直⇆线面垂直⇆面面垂直.这三者之间的关系非常密切,可以互相转化,从前面推出后面是判定定理,而从后面推出前面是性质定理,而线面垂直在三者中充当着承上启下的作用.

3.理由说明

图1

题目1(2008年高考文科湖北卷18题)如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1

(I)求证：AB⊥BC

(II)略.

图2

解析如右图,过点A在平面A1ABB1内作AD⊥A1B于D,则由平面A1BC⊥侧面A1ABB1,且平面A1BC∩侧面A1ABB1=A1B,得AD⊥平面A1BC.又BC⊆平面A1BC,所以AD⊥BC.因为三棱柱ABC-A1B1C1是直三棱柱,则AA1⊥底面ABC,所以AA1⊥BC.又AA1∩AD=A,从而BC⊥侧面A1ABB1,又AB⊆侧面A1ABB1,故AB⊥BC.

图3

评析此题需由已知的面面垂直证得线线垂直,中间必须要经过线面垂直这一环节,所以解析中的“作AD⊥A1B,得到AD⊥平面A1BC”就成了必经之路.

(2)重要性三种垂直之间的转换充分体现了这样一个动态的过程,我们在“转”的过程中需要不断明确转化的归属、去向、目标、目的地,从而以线面垂直为枢纽,实现三种垂直关系的不断转化.

题目2 (人教版必修2第二章2.3.1练习1)在三棱锥V-ABC中,V A=V C,AB=BC,求证：V B⊥AC.

解析如图,取AC的中点为M,连结V M、BM.由V A=V C,AC的中点为M,故V M⊥AC.同理,BM⊥AC.又V M∩BM=M,所以AC⊥面V BM,又V B⊆面V BM,所以V B⊥AC.

2005年，纽约南区的联邦检察长发出传票，指称美国国会多数党领袖比尔·傅利斯特 (Bill Frist)因涉嫌股票内线交易而遭调查。傅利斯特出身心脏外科医生，洁身自好，在朝野上下一度口碑甚佳，从政后也面临着如何出污泥而不染的考验。尽管长达18个月的外查内调后来无疾而终，这一事件对国会参、众两院的议员们都是一记不容忽视的警钟。

图4

点评(1)证明线线垂直往往化为线面垂直来解决,也即首先验证直线垂直于平面,从而得到这条直线垂直于这个平面内的所有直线.这是证明线线垂直的一条有效途径.(2)本题的转化过程：线线垂直→线面垂直→线线垂直.

题目3(人教版必修2第二章2.3.2例3)如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点,求证：平面PAC⊥平面PBC.

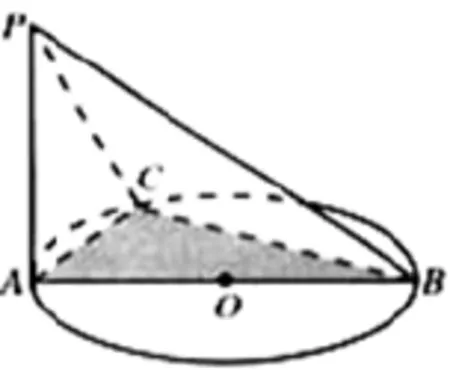
图5

解析由PA垂直于⊙O所在的平面,BC⊆面⊙O,所以PA⊥BC,又在⊙O中AB是⊙O的直径,所以AC⊥BC,而PA∩AC=A,所以BC⊥面PAC,又因为BC⊆面PBC,所以平面PAC⊥平面PBC.

评析由线线垂直⇋线面垂直⇋面面垂直可知,要证面面垂直需要从线面垂直入手要加以解决,即通过面面垂直的判定定理：如果一个平面经过另一个平面的垂直,则这两个平面互相垂直.而要得到线面垂直,又须从最基本的线线垂直入手来得到.

题目4(2016全国卷I文科第18题)如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连接PE并延长交AB于点G.

图6

(I)略;

(II)在图中作出点E在平面PAC内的正投影F(说明作法及理由).

分析探寻点E在平面PAC内的正投影F,即有EF⊥PAC.如何得到线面垂直?应该说有两种途径,一是由线线垂直得到线面垂直;二是由面面垂直得到线面垂直关系.由本题条件由面面垂直得到线面垂直是一种可行的思路,即寻找一个平面经过点E且与面PAC垂直,由已知条件易探寻出面PBA与面PAC垂直.当思考到这一点,我们要注意面面垂直向线面垂直转化过程中的条件：找交线、作交线的垂线等.故通过作EF⊥PA即探寻出点F的位置.

解析在平面PAB内,过点E作PB的平行线交PA于点F,F即为E在平面PAC内的正投影.

理由如下：由已知可得PB⊥PA,PB⊥PC,又EF//PB,所以EF⊥PC,因此EF⊥平面PAC,即点F为E在平面PAC内的正投影.

评析此问得分较低,主要原因是学生对该题设问方式的创新性(通过作图)不适应导致.但究其根本原因,还是在关键时候对三种垂直的“转换不灵”导致,此题只需抓住“PB⊥面PAC,通过平移(作平行线)的方式转换到EF⊥面PAC”.

综上所述,线面垂直“肩负着者上下起承转换”的重任,是空间三种垂直关系的中枢,学生一旦形成“以线面垂直为中轴,寻找其它垂直”的经验,就可在垂直关系的证明、空间距离、几何体体积等问题上大展身手.