对一类齐二次型最值问题的深究

浙江省宁波市第四中学(315016) 沈盈盈 魏定波

对一类齐二次型最值问题的深究

浙江省宁波市第四中学(315016) 沈盈盈 魏定波

一、问题再现

对任意不全为0的实数x,y,z,证明：

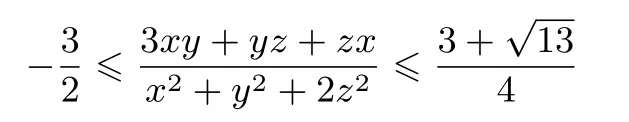
(第二届陈省身杯全国高中数学奥林匹克试题).

二、证明方法

评注对于这类最值问题,我们的解题方向是,借助变量x,y的对称性,以减少待定系数法运用中的参数个数,避免直接用基本不等式凑数法的不确定性.

例如,若实数a,b,c满足a2+b2+c2=1,则3ab-3bc+ 2c2的最大值为___.(2015浙江省五校联考试题.)

分析由3ab-3bc+2c2的结构,可以设

证法三(三角代换法)由于代数式3xy+yz+zx,x2+y2+2z2关于x,y对称,对于最大值来说,不妨设z≥0,x2+y2+2z2=1.于是有

评注对于类似上例关于x,y对称的不等式证明,通过基本不等式与三角函数的结合运用,避免了一些复杂方程的变换,不失为解决这类问题的又一个通性通法.

三、一般结论

定理1 对△ABC和任意的实数x,y,z恒有

证明设

由于

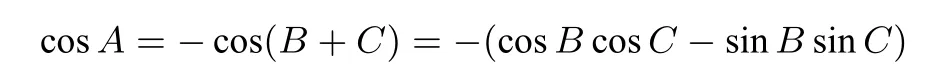
所以,

上式=[x-(zcosB+ycosC)]2+(zsinB-ysinC)2≥0等号成立的条件是：zsinB-ysinC=0且x-(zcosB+ycosC)=0.所以,不等式①成立,当且仅当

三式相加,即可证.在②式中,令a=b=1,得：

四、链接高数

我们用线性代数中的二次型的相关知识对这个问题进行解释.

定理n元二次型XTAX为半正定的充要条件是：矩阵A的各阶顺序主子式大于或等于零.

上述问题,等价于：

求f(x,y,z)=x2+y2+2z2-3axy-ayz-azx≥0恒成立的a的取值范围.

当XTAX为半正定,即

恒成立,由

[1]刘小东.也谈“怪异”不等式的证明[J].中学数学教学参考.2015(11)：40-41.

[2]姜坤崇.证明陈省身杯一赛题的简单实用方法[J].数学教学. 2015(10)：36-38.