玩转长方体 突破三视图

华南师范大学附属中学南海实验高级中学(528200) 孔小琼

玩转长方体 突破三视图

华南师范大学附属中学南海实验高级中学(528200) 孔小琼

三视图是新课程高考的一个新增内容,高考试题主要围绕空间几何体的结构特征、空间几何体的三视图以及表面积和体积等运算,核心考查学生空间想象能力及运算能力.《课程标准》对于空间几何体要求让学生经历“实物模型—三视图—直观图”这一相互转化的过程认识空间几何体.笔者在教学实践中发现,学生在解决这类问题上能力差异较大.空间想象能力稍好的学生,能通过自己的理解和想象顺利地解决问题,而对于能力较弱的学生来说,解决此类问题只能“碰运气”.有没有解决这类问题显化的、可操作性的通法呢?不妨回到三视图的定义,通过对定义的本质再认识去寻找答案.

所谓三视图,就是光线分别从几何体的前面向后面、左面向右面和上面向下面三个方向正投影,得到的投影图.一般地,侧视图在正视图的右边,俯视图在正视图的下边,它们都是平面图形,常用“长对正、高平齐、宽相等”来描述其数量关系.所以,给出了几何体的三视图,就从宏观上知道了“几何体的长、宽、高”,也就是说,以三视图中给出的几何体的长、宽、高可以构造出包含该几何体的最小长方体.有了长方体这样一个载体,接下来只需分别根据正视图、侧视图、俯视图的形状,按部就班地对长方体进行“切割”,最终获得几何体的直观图.因此,在解决三视图问题时,借助长方体可以有效解决一类三视图问题.

图1

例1 (2014年新课标卷I,理12)如图2,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的几条棱中,最长的棱的长度为( )

图2

分析本题以三棱锥的三视图为背景,计算其最长的棱长为素材创新设计,需要考生先根据三视图画出几何体,再计算各棱长.直接还原几何体需要考生具有较强的空间想象能力,但根据三视图中的网格和直角三角形两个显著特征,若以正方体为载体,可以帮我们较好的识图、想图和画图.

第一步,根据给出的三视图的数量关系,构造一个棱长为4的正方体;第二步,分别根据正视图、侧视图、俯视图的形状对正方体进行相应的切割,使切割后的几何体三视图与已知相符;第三步,画出直观图,得到如图的三棱锥A-BCD(其中A为正方体其中一条侧棱的中点).在正方体中由勾股定理易计算出六条棱长分别为因此,最长的棱为AD=6.

图3

例2 (2008年新课标卷,理12)某几何体的一条棱长为在该几何体的正视图中,这条棱的投影是长为的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为( )

分析可结合长方体的对角线在三个面的投影来理解计算,问题迎刃而解.如图,设长方体的高宽长分别为x,y,z,根据题意构造对角线则棱AC1在正视图中的投影为在侧视图中的投影为C1D=a,在俯视图中的投影为AC=b.则解得y=1,又所以(a2-1)+(b2-1)=6,解得a2+b2=8,从而(a+b)2=a2+2ab+b2=8+2ab≤8+a2+b2=16,得a+b≤4,当且仅当a=b=2时等号成立.故a+b的最大值为4.

图4

本题最大的特点是用文字语言描述三视图的特征,需要将其转化为具体的直观图.这其中最困难的是几何体的特征需要从文字描述的关系中获得,试题对能力的要求比较高：第一,要求考生有较高的阅读理解能力,能把题目的条件和所求读懂;第二,要求考生有较强的转化能力,能把文字的语言转化为图形语言;第三,要求考生有较好的空间想象能力,能根据三视图想象出该几何体;第四,要求考生有较强的逻辑推理能力,能根据不等式的性质对基本不等式进行变形和转化;第五,要求考生有一定的计算能力,能抓住图形中的数量关系并进行运算.借助长方体这一载体后,找投影、勾股定理、均值不等式等相关知识点自然就串联了起来,陌生的问题化归为熟悉的问题.

在三视图的教学中,建议深入挖掘正方体,在正方体中设计出探究活动,有效培养学生的空间想象能力.在教学中可设计如下两个探究活动：

探究活动1由正方体ABCD-A1B1C1D1(图5)可截得如图6至图10的几何体,分别画出这些几何体的三视图.

图5

图6

图7

图8

图9

图10

设计意图由正方体出发截得的几何体,学生画出其三视图较为容易,通过几何体的变化,一方面让学生养成依托正方体画三视图的习惯,另一方面可以让学生突破三视图的认识封闭,体会几何体和三视图之间的充要性.

学生作答图6的三视图为：

图11

图7的三视图与图6的三视图一致;

图8的三视图为：

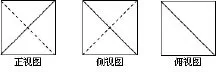
图12

图9的三视图为：

图10的三视图与图9的三视图一致.

由此还可以让学生体会：不同的几何体可以有相同的三视图,即说明三视图不能完全唯一表达一个几何体.如下面这道高考题：

例3 (2010年福建卷,理12)若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于___.

图14

分析给出的参考答案是显然是将该几何体视着底面边长为2的正三角形,侧棱长为1的直三棱柱进行求解.由此正视图就一定能确定该几何体是直三棱柱吗?其实容易看出,题目给出的三棱柱可以说斜三棱柱(有无穷多个),其表面积并不是常数,当然体积是定值,所以题目可以修改为求三棱柱的体积.

由此可以让学生进一步体会：一个几何体的位置确定之后,它的三视图是唯一的,但反过来,相同的三视图可以对应不同的几何体.稍有不慎,高考题都会犯错误,更需要我们有辩证的思考能力.

探究活动2 根据下列三视图还原该几何体.

设计意图在历年各省市的高考题中,不乏很多已知几何体的三视图求面积或体积的题目,下面的题目改编自模拟题或高考题,目的是让学生进一步体会借助正方体解决三视图问题.

图15

图16

图17

图18

学生作答依次还原几何体为：

图19

图20

图21

图22

认识柱、锥、台及其简单组合体的结构特征,能根据三视图识别和设计制作几何模型,这是《课程标准》要求考生具备的技能.三视图是立体几何中一个重要的概念,也是历年高考中的常考题,建议从对空间几何体的整体观察入手,认识整体图形,再以长方体为载体,培养识图、画图和想图能力.而长方体的面刚好可以起到投影面的作用,较好的帮助学生无图想图,有效的降低空间想象能力要求.而且我们通过将三视图具有的特征和原几何模型对照研究,将长方体中的三棱锥模型化,以及通过对不同类型三视图的分类处理,会有效地提高学生分析问题、解决问题的能力,更加有效的培养学生的逻辑推理能力.

[1]数学课程标准研制组.普通高中数学课程(实验)解读[M].南京：江苏教育出版社,2004.

[2]杨林军.宏观 本质 思维[J].数学通报,2015,54(12).