数学文化高考题举隅(I)*
北京丰台二中(100071) 甘志国
数学文化高考题举隅(I)*
北京丰台二中(100071) 甘志国
2016年10月8日,教育部考试中心公布了《关于2017年普通高考考试大纲修订内容的通知》(教试中心函〔2016〕179号).关于数学科目修订的内容主要是以下两条:
(1)在能力要求内涵方面,增加了基础性、综合性、应用性、创新性的要求,增加了数学文化的要求.同时对能力要求进行了加细说明,使能力要求更加明确具体.
(2)在现行考试大纲三个选考模块中删去“几何证明选讲”,其余2个选考模块的内容和范围都不变.考生从“坐标系与参数方程”“不等式选讲”2个模块中任选1个作答.
著名数学教育家、华东师范大学数学系张奠宙(1933~)教授在《数学教学》2015年第9期封底的“教育随笔”栏发表了文章《多一点数学文化的考题》[1],该文诠释了数学文化的内涵:“数学文化指数学的思想、精神、方法、观点、语言,以及它们的形成和发展.数学作为一种文化现象,早已是人们的常识.狭义的数学文化指数学的思想、精神、方法、观点、语言,以及它们的形成和发展;广义的数学文化除上述内涵以外,还包含数学家,数学史,数学美,数学教育.数学发展中的人文成分、数学与社会的联系、数学与各种文化的关系,等等.在即将公布的高中数学课程标准中给予了特别的重视,数学文化是一个单独的板块.”
本文将谈谈以前高考中出现过的数学文化试题的特点,旨在师生对2017届高考复习备考有所裨益.
1 以数学史为背景的数学文化高考试题
1.1 中国古代数学名著及数学家
题1 (1)(2011年高考湖北卷文科第9题)《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第5节的容积为( )

(2)(2011年高考湖北卷理科第13题)《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第5节的容积为___升.
解(1)B.(2)
这两道小题实质是同一道题,解法也相同:设这9节竹子自上而下各节的容积形成公差为d升的等差数列{an}(升),可得

评析在两千多年的世界数学发展史上,大数学家灿若明珠,数学著作浩如烟海,这些著作对世界科学的发展产生了深远的影响,比较起来,现在各国数学家普遍认为下面七部名著对数学的发展影响最大:
古希腊数学家欧几里得(公元前330年~公元前275年)的《几何原本》,中国古代的《九章算术》(其作者不详,大约成书于公元前3世纪至公元前1世纪,它的出现标志着中国古代数学体系的形成),阿拉伯数学家花拉子米(约780~约850)的《代数学》,法国哲学家和数学家笛卡尔(Rene Descartes,1596~1650)的《几何学》,英国科学家牛顿(Isaac Newton,1642~1727)的《自然哲学的数学原理》,瑞士数学大师欧拉(Leonhard Euler,1707-1783)的《无穷分析引论》,德国数学家和物理学家高斯(C.F.Gauss,1777~1855)的《算术研究》.
“竹九节”问题,就出自《九章算术》,考生见到该题,自然会从内心产生强烈的民族自豪感,所以该题也是对学生进行爱国主义教育的好材料.
这两道小题还是一对姊妹题,考查的知识点相同,都是等差数列的性质及通项公式的求法.
题2 (1)(2012年高考湖北卷理科第10题)我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一.所得开立方除之,即立圆径.“开立圆术”相当于给出了已知球的体积V,求其直径d的一个近似公式人们还用过一些类似的近似公式.根据π=3.14159···判断,下列近似公式中最精确的一个是( )

(2)(2013年高考湖北卷文科第16题)我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水,天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是___寸.
(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)
(3)(2014年高考湖北卷理科第8题即文科第10题)《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:“置如其周,令相乘也.又以高乘之,三十六成一.”该术相当于给出了由圆锥的底面周长L与高h,计算其体积V的近似公式它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式相当于将圆锥体积公式中的π近似取为( )

(4)(2015年高考湖北卷文科、理科第2题)我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮,有人送米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )
A.134石 B.169石 C.338石 D.1365石

(2)3.由题设可得,天池盆盆口的半径为14寸,盆底的半径为6寸,得盆口的面积为196π寸2,盆底的面积为36π寸2.

评析这四道题均出自于中国古代的重要数学著作,它们对考生的阅读能力有较强的考查;还对近似计算,球、圆台、圆锥的体积计算,分层抽样都有较好的考查.
题3 (2015年高考全国卷I文科、理科第6题)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图1,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )
A. 14斛 B. 22斛 C. 36斛 D 66斛

图1

题4 (2015年高考全国卷II文科、理科第8题)下边程序框图14的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a=()

图2
A.0 B.2 C.4 D.14
题5 (2016年高考四川卷理科第6题)秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图3所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为( )
A.9 B.18 C.20 D.35

图3
答案:B.(此题与2016年高考四川卷文科第8题实质一样,只是后者的选项变成了“A.35 B.20 C.18 D.9”.)
评析普通高中课程标准实验教科书《数学3·必修· A版》(人民教育出版社,2007年第3版)(下简称《必修3》)第34-45页讲述了“辗转相除法”和“更相减损术”、“秦九韶算法”、“进位制”这三个算法案例.以上题4,5考查的就是其中的内容.
秦九韶(1202~1261),生于山东,是南宋杰出的数学家,他所著《数书九章》中载有多项中国首创的、世界领先的重大数学成果,其中继承发展自刘益、贾宪以来的我国求高次方程近似解的“秦九韶法”与欧洲人的“霍纳-鲁菲尼法”相同,而且时间上“秦九韶法”要早五百多年.
题6(1)(2015年高考湖北卷理科第19题)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
如图4所示,在阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.
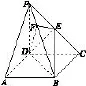
图4
①证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由.
②若面DEF与面ABCD所成二面角的大小为求的值.
(2)(2015年高考湖北卷文科第20题)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
在如图5所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,点E是PC的中点,连接DE,BD,BE.

图5
①证明:DE⊥平面PBC.试判断四面体EBCD是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由.
②记阳马P-ABCD的体积为V1,四面体EBCD的体积为V2,求的值.
答案(1)① 四面体DBEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB.②
(2)①四面体EBCD是一个鳖臑,其四个面的直角分别是∠BCD,∠BCE,∠DEC,∠DEB.②4.
评析该题又是出自我国古代的重要经典著作《九章算术》,同时该题也是立体几何的一道好题,注重基础常规,对空间想象能力和基本计算的考查到位.
1.2 阿波罗尼斯圆
题7 (2008年高考江苏卷第13题)若AB=2,AC=
解由于AB为定长,因此△ABC的面积由AB边上的高决定,而动点C满足AC=所以可如图6所示建立平面直角坐标系,求出点C满足的方程.

图6

评析可以证明:在平面内到两个定点的距离之比是不为1的正常数的点的轨迹是圆(这个圆就是阿波罗尼斯(Apollonius of Perga,公元前262~公元前190)圆).
普通高中课程标准实验教科书《数学2·必修·A版》(人民教育出版社,2007年第3版)(下简称《必修2》)第140页的例题“已知点P(2,0),Q(8,0),点M与点P的距离是它与点Q的距离的用《几何画板》探究点M的轨迹,并给出轨迹的方程.(答案:轨迹方程是(x-1.75)2+y2=1.252)”及第144页复习参考题B组第2题“已知点M(x,y)与两个定点M1,M2距离的比是一个正数m,求点M的轨迹方程,并说明轨迹是什么图形(考虑m=1和m/=1两种情形)”都是阿波罗尼斯圆的问题.
对于题7,考生若不知道其背景是阿波罗尼斯圆,就会用解三角形的知识来求解,运算量会大不少:

下面的题8~11的背景也都是阿波罗尼斯圆:
题8 (2006年高考四川卷理科第6题)已知两定点A(-2,0),B(1,0),如果动点P满足|PA|=2|PB|,则点P的轨迹所包围的面积等于( )
A.πB. 4πC. 8πD. 9π
答案:B.
题9 (2014年高考湖北卷文科第 17题)已知圆O:x2+y2=1和点A(-2,0),若定点B(b,0)(b/=-1)和常数λ满足:对圆O上任意一点M,都有|MB|=λ|MA|,则


题10 (2013年高考江苏卷第17题)如图7,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4.设圆C的半径为1,圆心在l上.

图7
(1)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
答案(1)y=3或3x+4y-12=0.(2)
题11 (2015年高考湖北卷理科第14题)如图8所示,圆C与x轴相切于点T(1,0),与y轴的正半轴交于两点A,B(B在A的上方),且|AB|=2.
(1)圆的标准方程为____;

图8

评析1)以上解答并没有用到题设“三点M,A,N共线”.
2)可把该题的结论推广为:若圆C与x轴相切于点T(1,0),与y轴的正半轴交于两点(a是已知的正数),则
(1)圆C的标准方程为

1.3 米勒问题
题12 (2005年高考天津卷文科、理科第20题)某人在一山坡P处观看对面山项上的一座铁塔,如图9所示,塔高BC=80(米),塔所在的山高OB=220(米),OA=200(米),图9中所示的山坡可视为直线l且点P在直线l上,l与水平地面的夹角为试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)?

图9
解可如图10所示建立平面直角坐标系xOy,可求得直线PA直线PA与y轴的交点T(0,-100).
可以证明“当且仅当过点B,C的圆与射线AP相切于点P(点P在第一象限)时,∠BPC最大”:
对于射线AP上不同于点P的点P′,设直线BP′交圆于点D,可得∠BP′C>∠BDC=∠BPC.由切割线定理,可得|TP|2=|TB|· |TC|=(100+220)(100+
评析在图10中,在射线AP上寻找点P使∠BPC最大的问题就是米勒(Joannes miiller,德国数学家)问题,其起源是米勒于1471年向诺德尔(Christion roder)教授提出的一个类似问题.

图10
下面的题13~16的背景也都是米勒问题:
题13 (2005年高考浙江卷理科第17题)如图11,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|:|A1F1|=2:1.

图11
(1)求椭圆的方程;
(2)若直线l1:x=m(|m|>1),P为l1上的动点,使∠F1PF2最大的点P记为Q,求点Q的坐标(用m表示).
解(1)(过程略).
(2)由米勒问题的解答可知,当且仅当过点F1,F2的圆与线l1相切时∠F1PF2最大(如图12所示).此时,设线l1与x轴交于点M,由切割线定理,可得|MQ|2=|TF1|·|TF2|=|m+1|·|m-1|=m2-1,|MQ|=所以点Q的坐标是

图12
题14 (2005年高考浙江卷文科第19题)如图13,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|:|A1F1|=2:1.

图13
(1)求椭圆的方程;
(2)若点P在直线上运动,求∠F1PF2的最大值.
解(1)(过程略).
(2)由米勒问题的解答可知,当且仅当过点F1,F2的圆与线l1相切时,∠F1PF2最大(如图2所示).

题15 (2010年高考江苏卷第17题)某兴趣小组测量电视塔AE的高度H(单位:m),如图14,垂直放置的标杆BC的高度h=4m,仰角∠ABE=α,∠ADE=β.

图14
(1)该小组已经测得一组α、β的值,算出了tanα=1.24,tanβ=1.20,请据此算出H的值;
(2)该小组分析若干测得的数据后,发现适当调整标杆到电视塔的距离d(单位:m),使α与β之差较大,可以提高测量精度.若电视塔的实际高度为125m,试问d为多少时,α-β最大?
解(1)略.

题16 (1986年全国高考理科第19题)如图15,在平面直角坐标系中,在y轴的正半轴(坐标原点出外)上给定两点A,B.试在x轴的正半轴(坐标原点出外)上求点C,使∠ACB取得最大值.

图15
解可设点A,B的坐标分别是(0,a),(0,b)(0<a<b).
由米勒问题解法可得,当且仅当过点A,B的圆与x轴的正半轴相切于点C时,∠ACB取得最大值.此时,由切割线定理可得|OC|2=|OA|·|OB|=ab,|OC|=所以所求点C的坐标是
1.4斐波那契数列
题17 (2013年高考北京卷理科第4题即文科第6题)执行如图16所示的程序框图,输出的S值为( )

答案:C.
评析笔者注意到运行图16所示的程序后得到的分数的分子和分母中出现的数1,2,3,13,21,610,987均是斐波那契 (Leonardo Fibonacci,约 1170~1250)数列{Fn}:1,1,2,3,5,8,13,21,34,55,89,···中的项(数列{Fn}由“F1=F2=1,Fn+2=Fn+Fn+1(n∈N∗)”确定),所以笔者发现了该题的背景是Fibonacci数列{Fn}:

斐波那契数列(也叫兔子数列,1963年美国创刊《斐波那契季刊》来专门研究该数列),即满足F1=F2=1,Fn=Fn-1+Fn-2(n=3,4,···)的数列{Fn}.普通高中课程标准实验教科书《数学5·必修·A版》(人民教育出版社,2007年第3版)第32-33页的阅读与思考《斐波那契数列》对该数列作了详细介绍,有不少高考题都是以该数列为背景的,比如下面的题18~21(其中的题18~20很好的考查了归纳推理).

图16
题18 (2011年高考湖北卷理科第15题)给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相连的着色方案如图17所示:

图17
由此推断,当n=6时,黑色正方形互不相连的着色方案共有____种,至少有两个黑色正方形相连的着色方案共有___种.(结果用数值表示)
解设按题设要求给n(n=1,2,···)个自上而下相连的正方形着色的方案数是an.当n≥3时,这种着色方案包括两种情形:(1)第1个正方形着白色,则后面的n-1个正方形的着色方案数是an-1;(2)第1个正方形着黑色,则第2个正方形着白色,后面的n-2个正方形的着色方案数是an-2.所以a1=2,a2=3,an=an-1+an-2(n=2,3,···),进而得数列{an}的各项依次是2,3,5,8,13,21,···,所以第一空填“21”.
因为给6个自上而下相连的正方形着黑色或白色的方案数是26=64种,所以第二空的答案是64-21=43.
题19 (1)(2009年高考福建卷理科第15题)5位同学围成一圈报数,规定:
①第1位同学首次报出的数为1,第2位同学首次报出的数也为1,之后每位同学所报出的数都是前2位同学所报出的数之和;
②若报出的数为3的倍数,则报该数的同学需拍手1次.已知甲同学第1个报数,当5位同学依序循环报到第100个数时,甲同学拍手的次数为____;
(2)(2009年高考福建卷文科第16题)五位同学围成一圈依序循环报数,规定:
①第一位同学首次报出的数为1.第二位同学首次报出的数也为1,之后每位同学所报出的数都是前两位同学所报出的数之和;
②若报出的是为3的倍数,则报该数的同学需拍手一次.当第30个数被报出时,五位同学拍手的总次数为___.
解(1)5.设所有人第n次报的数为Fn,则数列{Fn}为 1,1,2,3,5,8,13,21,34,55,89,144,···,Fn,···,F100由条件②知,只有所报的数是F4k(k∈N∗)时才拍手.
又因为甲报的数是F5l+1(l∈N),所以当且仅当两者均满足即甲报的数是F16,F36,F56,F76,F96时,甲才拍手,所以甲拍手的次数为5.
(2)7.解法同(1).
题20 (2012年高考江西卷理科第6题)观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,···,则a10+b10=( )
A.28 B.76 C.123 D.199
解C.可观察出数1,3,4,7,11,···的特点是后一个数总是它前面两个数的和,从而可算得答案.还可对此答案给予严格证明:由a+b=1,a2+b2=3,得2ab=(a+b)2-(a2+b2)=12-3=-2,ab=-1,所以a10+b10=(a5+b5)2-2(ab)5=112-2(-1)2=123.


当n=1时,已证命题成立.
假设当n=k时命题成立,即x2k>x2k+2.
易知x2k>0,得

即x2(k+1)>x2(k+1)+2,说明当n=k+1时命题也成立,所以要证结论成立.

评析题21(2)中的数列{Fn}就是斐波那契数列,这也说明高考题21(1)有此背景.
[1]张奠宙.多一点数学文化的考题[J].数学教学,2015(9):封底
[2]甘志国.高考压轴题(上)[M].哈尔滨:哈尔滨工业大学出版社,2015.28-29
(未完待续)
*该文为连载文章,共有三个部分,这是其中的第I部分—编者注.

