借力“三度开放”探究设计，点燃课堂思维之花

冷蓉晖

摘 要：在小学数学教学中，教师往往会运用各种课堂设计，以此激发学生的数学思维。随着信息技术和社会形态的多元发展，学校教育应当更加开放，以培养学生的创造性思维。本文根据教学实践，提出立足思路引领、自主过程、思维层次三个维度的开放探究，加强多元开放的数学课堂探究设计，培养学生解决问题的能力。

关键词：问题解决能力；开放性课堂；多元练习设计；教学策略

随着信息技术的发展，以及社会形态日益多元，学校教育也面临着创新和改革。笔者认为，教师应当立足思路引领、自主过程、思维层次三个维度的开放探究，给学生开放性的课堂探究机会，让学生经历探究过程，主动参与课堂探究，设计开放性的数学探究，由此培养学生问题解决的能力。现笔者根据自己在《平行四边形的面积》这一课的教学实践，谈谈体会和思考。

一、 借力思路引领探究

在小学数学教学中，依据新课标的要求，教师要培养学生数学猜想和实验的能力。然而在教学中，学生往往会根据自己的直觉做出胡乱的猜测和假设而忽略了实验验证。究其原因，主要是缺乏有序的数学思路，逻辑思维未能充分发挥作用。为此，教师要建立思路探究模式，设计开放性的数学练习，为学生提供丰富的现实背景，引导学生从不同的角度进行大胆猜想，让学生在观察、归纳、类比等逻辑推理的过程中培养创新思维的能力。

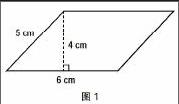
比如在教《平行四边形的面积》这一课时，笔者设计了一个开放性的数学练习：用多媒体展示一个长方形和一个正方形的小球场，问学生如何求出面积？刚一开始，笔者并没有告诉学生相关的数据，学生立刻指出，不知道长宽是多少，因此没办法求出。此时，笔者展示出一个方格图，并且告诉学生，每个方格的边长为1厘米，追问学生如何求面积。学生根据之前有过的求长方形、正方形面积的经验，认为可以将方格图覆盖在长方形和正方形上面，通过数方格的方式求出面积。在此基础上，笔者出示一个平行四边形（如图1）。已知平行四边形的长为6厘米，宽为5厘米，高为4厘米，笔者设置疑问：猜想一下，这个平行四边形的面积怎么计算呢？学生根据自己的经验进行大胆的假设，由于受到长方形和正方形面积计算的影响，提出了如下三种方法：6×5，6×4，5×4。在尊重三种假设的基础上，笔者引导学生思考：三种都正确吗？如何才能确定哪一种正确呢？学生提出，可以采用方格图的方法来进行验证。通过这一过程，学生认识到，假设是问题解决的第一步，必须要寻找方法进行验证，才能知道到底哪一种假设是正确的。借此时机，实际上教给了学生探究的思路，即“假设—验证”，为学生继续深入学习奠定了基础。

以上教学环节，教师借助多元化练习设计，从长方形和正方形的面积计算引入，带领学生对旧知进行回顾，并顺利过渡到新知，而后让学生根据已有经验展开猜想。在学生都有了假设之后引导探究问题解决的思路，从而帮助学生建构了数学探究的基本逻辑，为进一步发展学生的数学能力做足了准备。

二、借力自主过程探究

借助实验探究过程，可以提高学生的认知，判断数学猜想的真假性，并由此理解特例与归纳的内在关联，发展学生的数学推理能力。对于数学学科而言，实验并不是唯一的路径，但在小学数学教学中，引导学生进行实验探究，却能够帮助学生寻找到问题解决的思路和办法。

比如，在教学《平行四边形的面积》这一内容时，学生受到长方形面积计算的思维定式的干扰和影响，产生了思维的负迁移：认为平行四边形的面积等于两条邻边的乘积。显然，如何突破学生的这一思维困境，就成了课堂教学的重点和难点。为此，笔者立足开放的过程设计，带领学生放开手脚，大胆进行猜想验证。

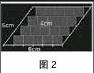
学生提出，可以用数方格的方法来进行实验，于是笔者将学生分为几个小组进行合作实验。有学生发现，用边长为1厘米的小正方形来铺满平行四边形，结果发现不能用到20个完全一样的正方形。这说明假设当中的5×4是不成立的（如图2）。

其他小组继续用小正方形来铺满平行四边形，结果发现，铺上28个小正方形时，整个面积大于平行四边形的面积。这个实验说明假设平行四边形的面积为5×6=30（平方厘米）是不正确的（如图3）。

那么，既然推翻了前两种假设，是不是第三种假设就一定正确呢？学生继续展开实验探究，借助剪切和拼接的方式，得到结论发现，平行四边形的面积正好是6×4=24平方厘米（如图4）。

在这个过程当中，学生找出了平行四边形一组对应的底边和高，并概括出平行四边形的面积等于底边乘高。那么，是不是实验到了这里就结束了？不然！这几个实验仅仅证明了一个特例，不具有普遍性。这个个例是否具有普适性，还需要进一步的归纳和推理来进行证明。为此笔者又设计了两个层次的开放性练习，让学生进行归纳和类比。笔者先出示了图5，让学生猜想这两个面积是否相等。

学生在课件演示下，认识到通过剪切、拼接的方式，将不规则图形转化为规则的长方形，并且面积不会改变。此时，学生在思想上已有了初步的认知。接着，笔者让学生通过小组合作展开实证，即将一个平行四边形转化为一个面积相等的长方形。学生分组展开，采用不同的剪切、拼接、移动的方法，顺利完成转化，并填写以下表格，进行比对（如表1）。

通过以上实证练习与不完全归纳，学生一步步逼近数学概念的本质，对平行四边形的面积有了更为直观的认知。

以上环节，教师借助过程的开放探究这一维度，让学生亲身参与，采集数据、分析数据、归纳推理，由此自主建构概念形成的过程，最终实现了“四基”的双向达成。

三、借力思维层次探究

对于小学生来说，基本知识的习得和基本技能的训练，都需要一定数量的练习才能达成，但传统经验已经向笔者证明，只有从不同思维层次的维度展开练习，才能打开学生的数学思路，发展学生的数学思维能力。

为此，在教学《平行四边形的面积》时，笔者特意设计了三个层次的练习，其目的是在帮助学生掌握基础知识的基础上进行变式练习，进而上升到开放性练习。基本练习主要让学生掌握平行四边形的面积计算公式，强化学生掌握底边乘高的基本原则（如图6）。而变式练习的目的，则是让学生全面贯彻理解这一基本概念。笔者设计了这样的习题：将一个长方形的木框，拉动变形，可以变成平行四边形，请问拉动前后，长方形和平行四边形有什么变化？学生借助这个变式练习，不仅有了再次动手操作的机会，而且能够再次强化平行四边形面积的教学难点，即通过直观呈现长方形和平行四边形拉动前后的变化，让学生直观感受到周长不变、面积变小的数学事实，深刻理解“变与不变”的内在关联。

在开放性练习中，笔者设计了这样的问题：在方格图上画一个面积为12平方厘米的平行四边形。针对这个问题，很多学生突破了练习的束缚，根据自己问题解决的思路，展开实验探究，这实际上是对学生的空间想象能力、发散思维力的一个挑战，也是深化学生数学思维的有效路径。根据已有学情，在四年级的时候，学生已经具备了画平行四边形的经验，但是因为长方形面积的长期思维定式的影响，学生不能深刻理解等底等高的平行四边形，受到这个认知的局限，也就不能有效地解决数学问题。为此，笔者追问学生：想象一下，如果是同一个底边，可以画出多少个平行四边形？学生循着这个思路，展开操作，很快得到启发，展开合作探究，认为可以就某一底或者某一高画出面积相同的平行四边形，也可以从不同的底边和不同的高着手，画出平行四边形来。由此，在小组合作中，学生画出来的平行四边形不仅数量众多，而且更加丰富，大大突破了封闭性题目的思维局限，提升了学生的创新思维。

以上环节，教师借助三个层次的多元设计练习，不仅循序渐进地带领学生巩固新知，同时在变式练习的基础上，为封闭性的思维体系注入了活水，有效地实现了课堂难点的突破，推进了学生发散性思维的深化。

总之，在小学数学教学中，开放作为一个有效教学的重要特征，不仅体现在习题的设计上面，更体现在课堂的思路引领、过程探究、思维层次三个维度上。笔者相信，只要以开放课堂为抓手，就一定能够牵引著学生的思维向纵深发展，进而提升学生的数学素养。