数学概念教学生活化的思考

祁燕丽

摘 要：根据小学数学500多个概念存在的五种不同类型的关系，总结出了从概念的“引入—建立—巩固—应用”一整套的教学模式，该模式具有提供丰富实例，创设生活情景，强调关键属性，重视实践应用，突出信息反馈五个特色。本文选出了与之匹配的五条教学策略，此策略旨在引入阶段要结合实际，借助充分的感性材料，在巩固阶段要重视变式、对比训练，在应用阶段要与生活接轨，在概念形成后，要及时纳入知识系统中使其融会贯通。

关键词：模式；特点；策略；生活化

一、问题的提出

概念是反映客观事物本质属性的思维形式。它是在对事物感性认识的基础上，经过分析、综合、抽象、概括等思维过程，区分事物的本质属性与非本质属性，把本质属性提取出来加以概括而形成的。每个概念都有自己的内涵和外延，内涵是指概念所反映的本质属性，外延是指概念所反映的事物范围。

小学数学中，有关概念共有500多个，主要有数的概念、数的关系方面的概念、几何形体的概念、量与计量单位的概念、比和比例的概念、统计方面的概念等九大类。它们的存在方式有五种类型：从属、同一、交叉、对立、矛盾。这些概念都来源于生活，都是现实世界中某一空间形式或数量关系的本质属性在人脑中的反映，反之，这些概念又指导着人们的实践生活。小学生由于生活经验积累少，感性知识贫乏，又受应试教育的影响，概念教育模式单一，面对高度抽象、概括、理性的数学概念，学生主要靠的是有意识地记忆，致使学生只会背概念，而不会运用所学概念去灵活解释生活中的数学现象、解决生活中的数学问题。

加强对数学概念教学生活化的探讨，使学用衔接、学以致用，是培养学生实践能力、创新能力的有效途径。

二、概念教学生活化的一般模式

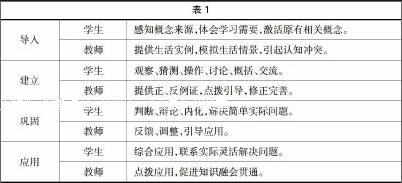
概念的学习主要通过以下两种途径获得：概念形成与概念同化。概念形成是从大量具体例子中抽象出事物的共同本质特征的过程，通常采用“直观→概括→具体化”的教学过程。概念同化是指利用认知结构中已有的知识来理解新的概念的过程，一般采用“旧知→同化→具体化”的教学过程。两种学习途径，最后都要落实到“具体化”上。所谓具体化，即把有实践得来的概念再拿到实践中去检验应用的过程。概念的具体化主要表现在：能否判断某一具体事物是否属于某一概念；能否举出属于某一概念的具体事物；能否举出不属于同一概念的具体事物等。如学习了长（正）方形的周长与面积后，可这样练习：操场四周围上栏杆是求面积吗？黑板的面积是指哪部分？给奖状做镜框，所需木条与玻璃是同一回事吗？可见，这里的具体化，很大程度上是生活化。尝试把两种途径有机地结合起来，经过四年的教学实践，初步形成了概念教学生活化的一般模式（如表1）。

这个概念教学模式，主要有以下特点：

·提供丰富实例——在概念教学中，离不开大量的反映概念本质特征的实例，教师的责任就在于选出最有助于学生形成概念的良好的实例，这个实例就必须来源于学生的生活经验、生活实际或原有知识。

·创设适当情景——注重为学生创设一个与新概念有关的有意义的生活情景，使学生能更好地再现与需要学习的概念有关的已有知识，为概念的形成、建立、应用创设有效平台。

·强调关键属性——概念教学的关键是要学生理清所学概念的关键属性。这个模式强调要求学生通过观察、猜测、操作、讨论、质疑、交流等课堂教学基本形式，学会舍弃非本质的属性，抓住概念的关键属性，理解和掌握所学概念的上位概念和下位概念。

·重视实践应用——应用是理解概念的最好方法。重视选择充分体现概念特性与多样性的正例和学生易混淆的反例，进行变式训练和对比训练，让学生不断地判断、辩论、概括，内化为自己的知识与技能。注重开放性训练和解决实际问题的能力训练。

·突出信息反馈——教学心理学证明：学习必须获得信息的反馈，没有反馈的学习收效甚微，甚至无效。在概念学习过程中，教师更要把握机会，及时肯定他们的猜测、操作、归纳等活动是否正确，不断修正完善。

三、概念教学生活化的策略

1. 导入概念要新、奇、快

布鲁纳说：学习的最好刺激，乃是对所学材料的兴趣，要想使学生上好课，就得千方百计点燃学生心灵上的兴趣之火。要想上好概念课，要想使学生对枯燥的概念感兴趣，导入必须新、奇、快。新：是指提供的学习材料要新颖，富有吸引力和挑战性。奇：是指能引起学生的认知冲突，能激起学生的求知欲和好奇心。快：是指导入要简洁明了，不要创设一种古怪复杂的“迷魂阵”，绕了半天还云里雾里。如：学习《分数的初步认识》，笔者手拿三个苹果和一把水果刀进教室，笑着问学生：今天老师来上课，你感到与往常有什么不同？学生说：老师拿来了苹果和水果刀。接着笔者拿出一只苹果，问：可用数字几表示？再拿出一个呢？再添一个呢？如果老师把一个苹果平均分成两份，这半个苹果用数字几表示呢？如果老师随便切一片，这一片能用■表示吗？学生原有的认知冲突与新现象产生了冲突，而且随着教学进度的推进，刚建立的认知结构与新现象又产生了冲突，思维的大门被一扇一扇开启了。又如：学习“圆的认识”，笔者上课第一句话就是：伟大的数学家、美学家毕达哥拉斯说，世界上最美最美的图形是——圆，这节课我们就一起来认识圆。

2. 建立概念要加强变式训练

所谓变式，就是提供给学生的各种感性材料不断变换其表现形式，使非本质属性时有时无，而本质属性始终保持不变。如：角的认识，展示的角要有不同位置不同角度的，角的边要有长有短的，让学生清楚地看出每个角的特征。如应用题题目的数量关系不变，取材变来变去，叙述方式换来换去都一样，不要被“换汤不换药”的把戏所迷惑。

如学习了长方形、正方形后，先让学生说一说它们的特征，再让学生辩一辩为什么正方形是特殊的长方形。用自己的语言来阐述理由，在阐述的过程中，学生越辩越清，不被表面现象所迷惑，从而更好、更深刻地掌握长方形、正方形的特征以及它们的异同。当学到平行四边形的时候，同样可以这样提问——为什么说长方形是特殊的平行四边形。

3. 巩固概念要重视比较训练

烏申斯基指出：“比较是一切理解和思维的基础。”一个数学概念一旦建立后，要重视对比训练，尤其是一些易混淆的概念。最好用生活中看得见、摸得着的事例去分析错误原因，尝试进行矫正。从正反两方面、横纵两侧面进行训练，让学生真正弄清概念的内涵和外延，及时反馈，及时点评。

如“时间、时刻”“质数、质因数、因数、互质数”“增加、增加到、增加了”等。如果说变式是从材料方面促进理解的话，那么比较则是从方法方面促进理解。如为帮助学生建立倍的概念，可以设计如下练习：（1）有5个□，○的个数是□的7倍，○有多少个？（2）有16个□，□的个数是○的2倍，○有多少个？（3）有56个□，8个○，□的个数是○的多少倍？

4. 应用概念要突出与生活接轨

现代教育理论认为，教育的目的在于发展，能力的核心是思维，思维的基础是实践。苏霍姆林斯基说过：“把知识加以运用，使学生感到知识是一种使人变得画龙点睛高起来的力量，这是兴趣的重要来源。”是啊，学习了一个新概念，学生正兴奋不已，跃跃欲试，为什么不放手让学生在实践中露一手呢？如学了计量单位后回家去看一看、比一比，哪些东西标有kg、g、l、ml等；学了几何方面的概念后，动手去量一量、做一做；学了百分数后去试着解释电视新闻中播出的“今年第一季度工农业总产值比去年同期增长了2.8个百分点”是什么意思，帮妈妈算算利息、本息、保险费等。只有这样，学生所学的概念才具有活力，才能真正提高学生的实践能力与创新能力。

5. 新概念形成后，要及时把它纳入知识系统中，以利于沟通相关概念之间的联系

如：学了乘法分配律后，就要与乘法交换律、乘法结合律进行比较，搞清它们之间的联系与区别。学了比例的基本性质后，就要与商不变的性质、分数的基本性质相沟通，使知识横成块，纵成线。

数学概念多而且抽象，有的概念与概念之间极易混淆，如何创设生活情景，提供给学生丰富、典型、具有研究价值的生活实例，还需要进行仔细深入的研究探讨。只要心中装着学生，做生活的有心人，就一定能让枯燥的概念教学生动具体化、形象生活化。