多元视角，探寻高中数学解题捷径

☉江苏省苏州实验中学 缪海峰

多元视角，探寻高中数学解题捷径

☉江苏省苏州实验中学 缪海峰

数学解题是高中数学“教”与“学”的重要内容，在处理一道数学问题时，思路不同，解题方法自然不同.“常规”解法是按照一般的思路进行解题，是基础，是重点，是雪中送炭；“简捷、技巧”解法都是按照特殊思路进行解题，是提高，是难点，是锦上添花.实践表明，只有切实掌握基本方法、基本技能，灵活运用，准确把握“常规”，才能有“技巧”；抛开“规”只想寻“巧”是不切实际、毫无意义的.因此，在掌握“常规”解法的基础上，适时探寻捷径，能够有效提升学生观察能力、思维创新能力、分析问题和解决问题的综合能力.本文借助于几道典型案例进行剖析，重点阐述从多角度探寻高中数学解题捷径的具体措施，以飨读者.

一、细心观察，让解题捷径“应运而生”

观察能力是学生进行数学解题的重要保障，也是提升学生能力的窗口.高中数学习题并不是盲目地套公式，缺乏细致地观察分析具体题目的特征，难以获取数学解题的捷径；相反，若能够细心观察、仔细挖掘内在本质特征，往往能自然而然地获取解题的简捷途径与方法.

例1已知方程（ac-bc）x2+（bc-ab）x+（ab-ac）=0存在两个相等的根，试证明可组成等差数列.

剖析：此题属于难度适中的基本题，常规处理的方法是：根据题意中“存在两个相等的根”，可令Δ=0，结合配方手段进行分解因式，从而得出要证明的结论，显然这种思路比较复杂、烦琐！如果我们细心观察不难发现，给出的方程中存在“系数之和为零”的显著特征，借助于这个特点，可以巧妙地证明此题.

证明：根据观察发现，（ac-bc）+（bc-ab）+（ab-ac）=0显然存在一根为1，由于原方程存在相等的根，则两根均为1；根据韦达定理可知=2，即2（ac-bc）= bc-ab，即2ac=ab+bc，故

评析：上述案例中，主要是根据方程系数之间存在一定的特殊关系（各项系数和为零），结合题设条件得出两个相等根均为1，从而获取巧法.可见，从题设条件和题目给出的结论特殊关系上，进行仔细观察能够出“捷径与巧妙解法”，提醒我们教师在教学中应该引导学生增强这方面的意识.

二、活用概念，让解题捷径“水到渠成”

数学概念是数学教学中的主要内容之一，数学概念的理解与应用是掌握数学基础知识、基本技能的前提，有助于获取数学解题的捷径，有助于提升处理数学问题的实际能力.实践表明，高中学生在数学学习中，往往容易忽视对数学概念的透彻理解与应用，导致舍近求远、舍巧求拙的情形出现.

例2如图1所示，线段AB长为L，且两端点A和B均在抛物线上移动，点M为线段AB的中点，试求：当M距离x轴最近时的纵坐标.

图1

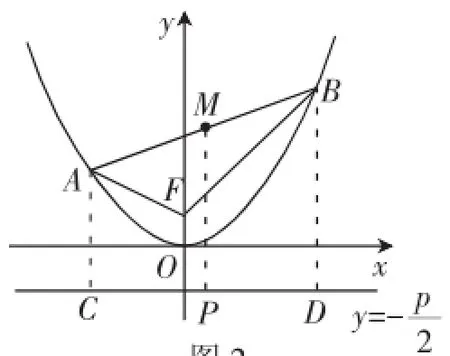
图2

分析：本题侧重于考查圆锥曲线方面的数学知识，常规思维是先求出动态线段AB的中点M的轨迹方程为f（x，y）=0，在此基础上求出纵坐标y的最小值.显然，这种处理方法的运算过程比较复杂，耗时且解题的正确率不高，解题效率比较低下.若从抛物线的定义出发，将梯形中线段关系有效转化成三角形的三边之间的关系，再利用两点之间线段最短的原理得出结论.

解析：根据题意作出抛物线的准线，如图2所示，根据抛物线定义可知

评析：上述案例中主要利用抛物线的概念和定义，大大简化了直接选择代数法处理问题的烦琐计算，体现思路清晰、步骤简捷的特征，能够有效拓展锻炼学生思维的深度与广度，提升处理问题的能力.

三、广泛联想，让解题捷径“顺理成章”

学生思维的拓展离不开丰富的联想，联想是思维的重要手段，也是数学解题分析的动力.在解题中，将数学知识与题目特征结合在一起，从不同角度进行广泛联想，往往能获取各种不同的解法，能够有效打破题目形式所限，不致于在几个数学定理和公式中打转，方便探寻优化解题的方案.

例3如图3所示，在⊙O：x2+y2=r2外存在一点Q（a，b），现过Q点作⊙O的割线交圆于A、B两点，试求：弦AB的中点P的轨迹方程.

图3

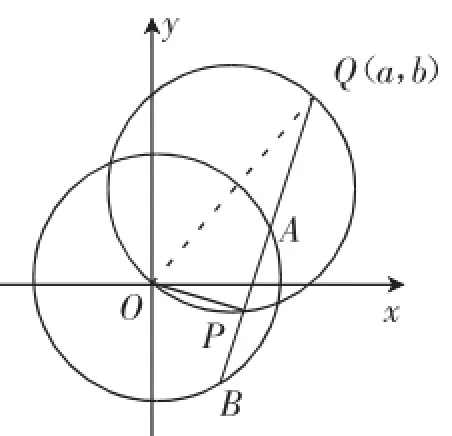
图4

分析：本题关于圆锥曲线问题，常规的处理手段是“设点、列方程、代换、化简”等求解轨迹方程的步骤，显然是比较麻烦的.若依据题目几何特征进行思考与联想，容易发现P点为AB的中点，OP⊥AB，则中点P的轨迹为以OQ为直径的圆（如图4所示），此处理方法简捷、易懂.

解析：根据题意可令弦AB的中点P（x，y），由于OP⊥ AB，所以kOP·kAB=-1，即=-1，即x2-ax+y2-by=0，则弦AB的中点P的轨迹为圆：x2-ax+y2-by=0在⊙O：x2+ y2=r2内部的一段圆弧.

评析：本题属于典型的求轨迹问题，从上述分析和解析中可以发现，借助于纵横联想手段获取解题的捷径，提醒我们一线的高中数学教师，在平时课堂教学中，注重对学生广泛联想（纵横、结构、逆向、类比等）意识的引导，促进学生解题能力的进一步提升.

四、数形结合，让解题捷径“瓜熟蒂落”

数形结合是解决数学问题的重要思想方法，高中数学问题中，许多问题都可以采取以“形”代“数”的方式进行处理，能够将“数”的抽象转化成“形”的形象化、直观化，便于抓住问题的本质内涵，探寻解题的突破口，获取解题的捷径.

例4在平面直角坐标系中，第一象限内存在一等边三角形，其中两个顶点为（1，0）、（2，1），如图5所示，试求：此等边三角形的第三个顶点的坐标.

图5

图6

分析：常规的处理方法是假设第三个顶点的坐标（x，y），根据两点的距离公式结合等边三角形的边长和角度性质联立得到二元二次方程组进行求解x和y，此过程运算量较大，繁杂易错.若能充分考虑数形结合的数学思想方法，灵活运用复数的几何性质进行求解，大大简化解题过程.

解析：根据题意在复平面上构建等边三角形的三个顶点分别为Z1（1，0），Z2（2，1），Z3（x，y），如图6所示，复数形式表示为：Z1=1，Z2=2+i，Z3=x+yi.由于对应的复数运算为：（2+i）-1=1+i，可以用向量表示，则其中A的坐标为（1，1）；现将向量绕坐标原点O逆时针旋转60°后得到向量对应的复数为：（1+i）绕点Z1逆时针旋转60°后得到向量对应的复数运算为：（x+yi）-（1+0i）=（x-1）+yi.

点评：数形结合是数学学科的显著特点，由数向形的转化能够将抽象的数学问题变得形象化、直观化，便于学生的理解和接受，便于巧解方法的获取.高中数学解题中数形结合思想确实应该受到教师和学生的重视，尽可能地发挥其解题的强大功效.

总而言之，高中数学解题中应该有效挖掘题设中的基础知识、基本方法和解题技巧，作为一线数学教师积极引导学生探寻简捷、合理的解题方法，进而提升高中数学解题的效率和能力.