谈“转化思想”在三角函数教学中的妙用

广东省梅州市梅县区径义中学(514781) 熊永华

谈“转化思想”在三角函数教学中的妙用

广东省梅州市梅县区径义中学(514781) 熊永华

转化是数学中最常用的思想,通常由一种形式变为另一种形式,一个问题变化为另一个问题,由繁到简,由特殊到一般,最终解答问题的一种数学思想.在直角三角形的边角关系的教学中,从三角函数概念建立、推理认证、计算化简到实际问题的解决,始终贯穿着转化思想的运用,如利用三角函数定义可以实现边与角的转化；利用三角函数之间互余关系,实现对“正、余弦”间进行灵活地相互转化；利用添加辅助线,实现非直角三角形向直角三角形转化；利用根据题意画出图形,实现将现实问题向数学模型上转化等.

一、利用三角函数定义实现边与角的转化

在Rt△ABC中,若∠A、∠B、∠C的对边分别为a、b、c,且∠C=90°.

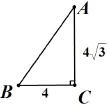
图1

要求出∠B的度数,根据已知条件,运用三角函数中的正切,可求出∠B的正切值,用特殊角三角函数值求出∠B的度数,从而利用三角函数的定义,由直角三角形中除直角外的已知边和角,求出所有未知的边和角,实现边与角的转化.

二、利用三角函数之间互余关系,实现对“正、余弦”间进行灵活地相互转化

因为直角三角形中两锐角互余,所以三角函数正弦、余弦存在cosA=sin(90°-A),sinA=cos(90°-A)、的等量关系,利用互余三角函数关系,实系“正、余弦之间”的转化,来解决数学问题.

三、利用添加辅助线,实现非直角三角形向直角三角形转化

例3. 如图所示,在四边形ABCD中,AB=2,CD=1,∠A=60°,∠D=∠B=90°,求此四边形ABCD的面积.

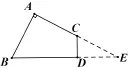
图2

解: 延长BC、AD相交于E.

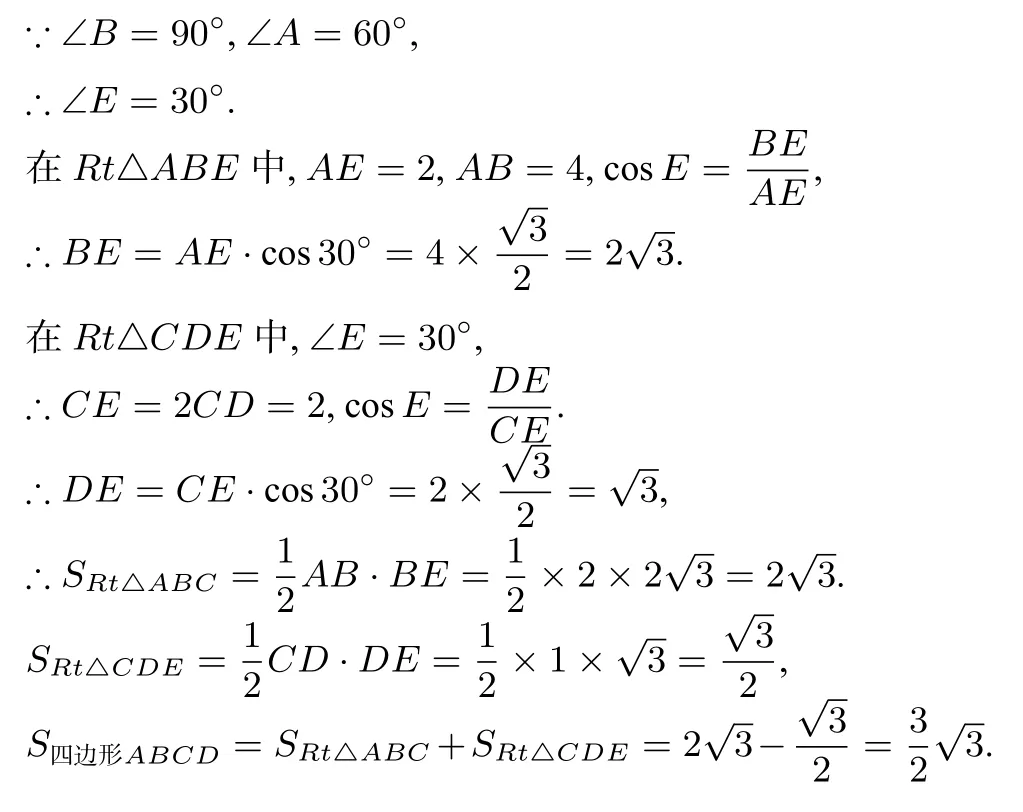
对于非直角三角形有关问题的解决方式,往往是通过作辅助线将它们补全或分割成直角三角形,从而利用直角三角形的有关性质和三角函数的知识来解决问题,此题四边形问题转化为三角形,尤其是转化为直角三角形的问题来解决,是数学思想中转化思想的又一体现.

四、利用根据题意画出图形,实现将现实问题向数学模型上转化

例4. 某水库大坝的横断面是等腰梯形,坝顶宽6米,坝高10米,斜坡AB的坡度为1: 2,现要加高2米,在坝顶宽度和斜坡坡度均不变的情况下,加固一条长为50米的大坝,需要多少土石料？

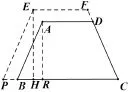
图3

解: 根据题意,画出图形,过E作EH⊥BC于H.

∵梯形EPCF为等腰梯形,∴PC=2PH+EF,

∵梯形ABCD为等腰梯形,AR⊥BC,

∴BC=2BR+AD.

∴V=50(S梯形EPCF-S梯形ABCD)=50×(360-260)=5000(立方米).

有关大坝加固的问题是近几年较常出现的数学问题,这些题往往图形较为复杂,计算步骤较多,有一定难度.解此类题,首先应根据题意画出相应图形,将现实生活中的事例转化到数学问题上来,再者是建立数学模型,找出变量(如坝高增加2米)和不变量(如斜坡坡度,四边形形状仍为等腰梯形),利用三角函数坡度即是解决本题的关键.

实践证明: 在直角三角形边角关系的教学课堂中,运用转化思想,进行问题间的转化,使问题由繁到简,由特殊到一般,能更好地培养和提高学生的解题能力和发散逻辑思维,从而达到教学目的.