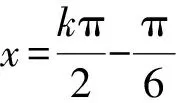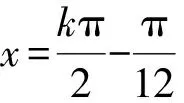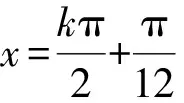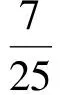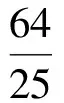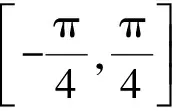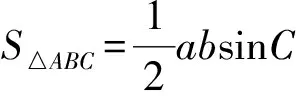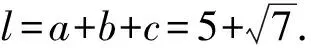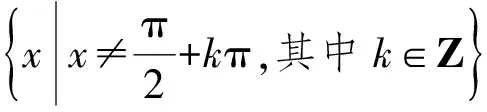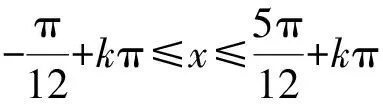例谈高考三角函数复习备考策略*
●曲文瑞 (平湖中学 浙江平湖 314200)
例谈高考三角函数复习备考策略*
●曲文瑞 (平湖中学 浙江平湖 314200)
三角函数是中学数学中非常重要的组成部分,它既是对前面函数知识的延伸,又是三角形知识的拓展,同时也是历年来考试的热点.因此在学习及备考中必须要抓住三角函数的本质,把握好三角恒等变换的方向,以提高三角函数复习的备考质量.
三角函数;解三角形;等价转化
1 知识内容
在高考中,三角函数考查的主要内容包括:三角函数的定义、三角函数的图像和性质、三角恒等变换及运算、三角函数与解三角形的知识交汇.解三角形考查的主要内容包括:正弦定理、余弦定理、三角形内角和定理及三角形面积公式的应用.
2 课后反思
本节课的设计是先让学生总结解题的基本方法,再以一题多解促进学生尽可能穷尽解题方向,再把图7进行旋转演变成2015年浙江省宁波市中考压轴题,引导学生解决.整堂课的设计简洁明了,没有精彩的情境引入,也没有华丽的多媒体展示,但学生整堂课学习下来兴致盎然,关键是抓住了课堂的根本.
2.1 以问题引领课堂
本堂课中,教师充分发挥引导者作用,为学生提供了3个互相关联、层层递进的问题,生动地诠释了以学为中心的教学理念,为初三的复习课打开了一个从基本图形出发、让学生经历综合题的生成过程的基本思路.同时,相似三角形的知识始终贯穿课堂,主题明确,本质清晰.
2.2 以联想拓展思维
整堂课以相似三角形的线段比为知识原型,以共有一个顶点的2个相似三角形为基本图形,积极引导学生在现有的问题上去发现所有的解题方向,对知识点的联想,对思想方法的联想,从图形的静态变化到动态旋转,不断发散学生的思维,不断诱发学生从已有的图形进一步向上拓展,再通过解决问题去丰满、完善已有的知识,真正做到了以学生为主体的课堂教学.思维的激荡让教师的引导更加有效,从而激起了学生求知、探究的欲望,使整个课堂变得生动起来.
2.3 以实例调适心态
整堂课提供了3个问题,由易到难,层层递进,引导学生归纳总结基本解题方法并熟练掌握.由于最终演变得到的是一道中考压轴题,因此大大激发了学生的成就感和获得感.由于前面做足了铺垫,很多学生在课堂氛围的带动下,最终找到了解题的方案,攻克了平时没有头绪的难题.课堂上的成功让他们感觉到原来中考压轴题也是用基本方法解决的,无形中消除了惧怕心理,有利于学生以平常的心态应对解决中考难题.中考压轴题的难点在于图形比较复杂,解题分析中容易受到各种干扰,因此突破的关键是平时对所研究的一些重要的基本图形的结构与性质烂熟于心,形成基本模型,这样才能从较复杂的图形中分离出基本图形,迅速进行解答.
2 命题分析
三角函数是中学数学中一种非常重要的函数,是浙江省数学高考对基础知识和基本技能考查的重要内容.在2016年的浙江省数学高考中,三角函数内容文、理科均考了2个小题和1个大题,所占分值为25分,但考题难度不大,均属于中等难度题.复习时,除了要重视三角函数的必考点(三角恒等变换)、重点(三角函数的图像和性质)、热点(三角函数与解三角形的知识结合)外,还应深刻领会三角函数中所蕴含的数学思想(数形结合、转化与化归、整体思想、换元思想).
3 典例剖析
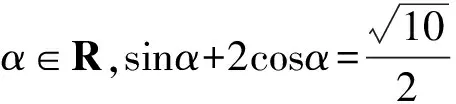
( )

(2013年浙江省数学高考理科试题第6题)
解法1 (方程思想)由
得


于是

进一步
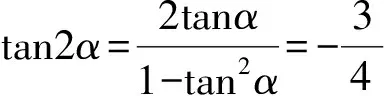
点评 此法主要是从同角三角函数的基本关系入手,构造方程组,直接解出sinα,cosα.此题还可以利用




化简得
3tan2α-8tanα-3=0,

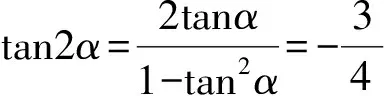
点评 此法主要是利用齐次式直接求出tanα,进而求得tan2α.
解法3 (引入辅助角)因为

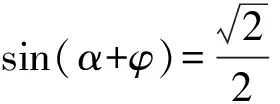

或

故
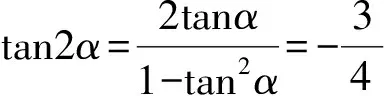
点评 此法主要是利用辅助角公式,解得α与φ的关系,通过φ的正切值求得α的正切值.
例2 在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB.
1)证明:A=2B;

(2016年浙江省数学高考理科试题第16题)
1)证法1 (从正弦定理入手)由正弦定理得
sinB+sinC=2sinAcosB,
从而 2sinAcosB= sinB+sin(A+B)=
sinB+sinAcosB+cosAsinB,
于是
sinB=sin(A-B).
又A,B∈(0,π),从而
0 于是 B=π-(A-B)或B=A-B, 即 A=π(舍去)或A=2B, 故 A=2B. 证法2 (从余弦定理入手)由余弦定理得 从而 bc=a2-b2, 于是 b+c=2acosB, 即 亦即B为锐角,因此 又bc=a2-b2,故 所以 cosA=cos2B, 故 A=2B. 点评 已知式中既含有边又含有角,证法1和证法2利用正、余弦定理进行等价转化,实现边角统一,然后再进行处理,水到渠成. 证法3 (从射影定理入手)在△ABC中,c=acosB+bcosA,又b+c=2acosB,从而 b+acosB+bcosA=2acosB, 于是 b=acosB-bcosA. 又b=acosC+ccosA,从而 acosC+ccosA=acosB-bcosA, 由正弦定理得 sinAcosC+cosAsinC=sinAcosB-cosAsinB, 于是 sin(A+C)=sin(A-B), 即 sinB=sin(A-B). 又A,B∈(0,π),从而 0 于是 B=π-(A-B)或B=A-B, 即 A=π(舍去)或A=2B. 故 A=2B. 证法4 (恒等变形为二倍角正切关系)由正弦定理得 sinB+sinC=2sinAcosB, 从而 2sinAcosB= sinB+sin(A+B)= sinB+sinAcosB+cosAsinB, 即 sinAcosB=sinB+cosAsinB=sinB(1+cosA), 于是 sinAcosB=sinB(1+cosA), 即 亦即 因为sinB≠0,所以 sinC=cosB, 又B,C∈(0,π),于是 解法2 (从正弦定理入手进行等价转化)由正弦定理及A=2B,得 从而 a=2bcosB. 2bsin3B=a=2bcosB, 即 sin3B=cosB. 又A,B∈(0,π),从而 即 故 1)求f(x)的最小正周期; 分析 欲求f(x)的最小正周期、最值,首先要将f(x)化为y=Asin(ωx+φ)+B的形式. 解 1)由已知得 点评 本题主要考查两角和与差的正弦公式、余弦公式、二倍角公式,三角函数的最小正周期、单调性,以及基本运算能力. 例4 在△ABC中,内角A,B,C所对的边分别是a,b,c.已知acosB=bcosA,边BC上的中线长为4. 2)求△ABC面积的最大值. (2016年浙江省高三数学测试理科试题第16题) 1)解法1 (从正弦定理入手)由acosB=bcosA及正弦定理得 sinAcosB=sinBcosA, 从而 sin(A-B)=0, 于是 故 由余弦定理得 解得 解法2 (从余弦定理入手)由acosB=bcosA及余弦定理,得 整理得a=b,从而 令边BC上的中线长AD=4,在△ABD中,由余弦定理得 从而 于是 即 82+a2=2(b2+c2)=2(a2+3a2), 从而 于是 即 2)解法1 (转化为角A)由第1)小题得A=B,从而 c=2acosA, 及 解得 于是△ABC的面积 解法2 (转化边)由A=B,a=b,在△ABD中,由余弦定理得 从而 于是△ABC的面积 在△ABD中, 解得 解法3 (转化为角C)由A=B,a=b,在△ABD中,由余弦定理得 从而 于是△ABC的面积 因此 进而 9S2≤322, 即 当且仅当sin(C+φ)=1时等号成立. 解法4 (利用基本不等式)由第1)小题的解法3知 82+a2=2(b2+c2)=2(a2+c2), 从而 a2+2c2=64. 设边AB上的高线长为h,则 ( ) ( ) ( ) ( ) ( ) A.11 B.9 C.7 D.5 7.方程3sinx=1+cos2x在区间[0,2π]上的解为______. 8.△ABC的内角A,B,C对边分别是a,b,c,已知2cosC(acosB+bcosA)=c. 1)求c; 1)求f(x)的定义域与最小正周期; 1)证明:a+b=2c; 2)求cosC的最小值. 参 考 答 案 1.B 2.D 3.A 4.C 5.B 8.解 1)在△ABC中,由正弦定理化简可得 2cosC(sinAcosB+sinBcosA)=sinC, 整理得 2cosCsin(A+B)=sinC. 因为角A,B,C为△ABC的内角,所以 sinC≠0,且sin(A+B)=sinC, 因此 又0 2)在△ABC中,由余弦定理得 c2=a2+b2-2abcosC, 即 从而 ab=6, 于是 (a+b)2-18=7, 即 a+b=5, 所以f(x)的最小正周期为π. 10.1)证明 由题意知 化简得 2(sinAcosB+sinBcosA)=sinAsinB, 即 2sin(A+B)=sinA+sinB. 因为A+B+C=π,所以 sin(A+B)=sin(π-C)=sinC, 从而 sinA+sinB=2sinC, 故由正弦定理得a+b=2c. ��2016-12-29; 2017-01-30 曲文瑞(1977-),女,吉林德惠人,中学高级教师.研究方向:数学教育. O124 A 1003-6407(2017)03-42-06
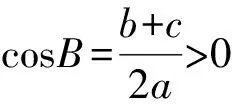


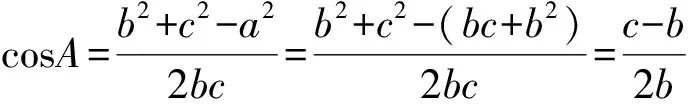

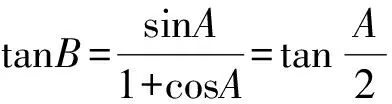
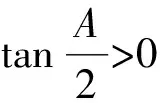
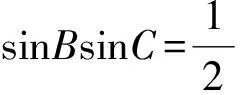

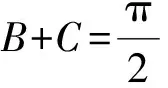

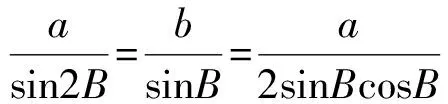
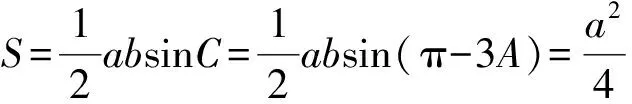
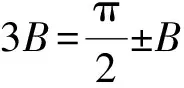


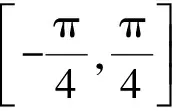

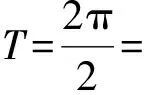



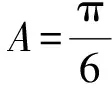



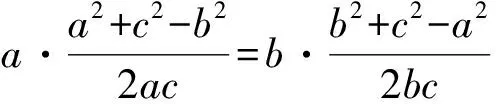


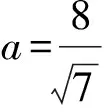


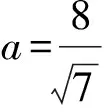





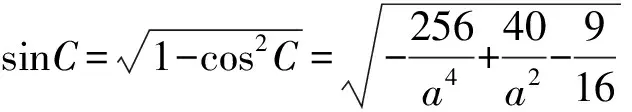




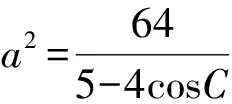
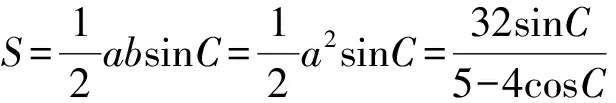





4 精题集萃