如何促进学生数学地思考——基于陶维林老师的课堂教学分析*

●求莲萍 叶国芳 (嵊州中学 浙江嵊州 312400))

如何促进学生数学地思考
——基于陶维林老师的课堂教学分析*

●求莲萍 叶国芳 (嵊州中学 浙江嵊州 312400))

在数学课堂教学中，如何促进学生数学地思考，如何为学生数学思考提供机会，这是非常重要的.基于对陶维林老师“基本不等式”一课的分析，发现陶老师在促进学生数学思考上的一些有益的做法：少而精的课堂问题驱动、教师表述与板书，这不仅为学生的数学思考提供了框架，也提供了学生冷静思考的时间与空间.

学生；数学思考；课堂教学

2015年6月的一天，笔者所在学校迎来了一位尊贵的客人——南师大附中的数学特级教师陶维林老师.陶老师是人民教育出版社新课标教材的参编者，也是新课程教材培训的讲师团成员，他10多年前写的《几何画板教程》已成经典.陶老师虽年届七旬，但精神抖擞，思维敏捷,并亲自为青年教师们上了一堂示范课——“基本不等式”.课上得很成功，对青年教师们的震动很大，大家感觉茅塞顿开，惊呼“课原来可以这样上”，纷纷撰文书写体会，效仿实践.那么，陶老师的课到底是如何上的，特色在哪呢？

1 课堂简录

上课伊始，师生互致问候后，教师借助多媒体展示问题1.

问题1 大家学习等差数列与等比数列时，曾经接触到2个重要概念——等差中项、等比中项.2个数的等差中项与等比中项哪个大？

问题1展示后，学生没动手，教师提示后，学生开始动手演算.在学生独立思考、演算后，教师请学生回答.

生1：等差中项大于等比中项.

(学生有的赞同，有的不赞同.教师请其中1位不赞同的学生回答.)

生2：等差中项大于等于等比中项.

(部分学生赞同.)

师：有不同的答案吗？

(有4位学生举手，教师请其中1位学生回答.)

生3：当2个数为负数时，它的等差中项为负数，等比中项为正数，等比中项大于等差中项.

(部分学生赞同该想法.)

师：等差中项和等比中项哪个大？首先，什么叫做2个数的等差中项？什么叫做2个数的等比中项？这2个概念都没搞清楚，怎么可能去判断哪个大呢？比如：2和-4，它们的等比中项是什么？

(学生齐答：没有.)

师：那么这个问题的前提条件是什么？知道的请举手.数学是玩概念的，不是玩技巧的.若概念不清楚，怎么能把数学学好呢？

(学生齐答：这2个数应同号.)

师：首先这2个数是同号的.第2个问题：2个同号的数的等比中项是什么？比如a和b，这2个数的等比中项是什么？

(教师沉默，给学生一定的时间思考、演算，然后师生一起归纳，教师板书结果如下：

师：好，现在知道这个问题应该怎么分析了吧，首先要把概念搞清楚，然后分类讨论.今天我们主要讨论第1种情况，即2个数都是正数的情况……

(教师借助多媒体呈现以下内容：

师：你能用文字语言来表述这个不等式吗？

生4：2个正数和的一半大于等于2个正数……

(学生回答遇困.)

师：“2个正数和的一半”描述得很形象，我们把它称为算术平均.还可以怎样描述？

生5：2个正数的算术平均大于等于这2个正数的几何平均.

师：2个正数的算术平均大于等于这2个正数的几何平均.或者说2个正数的算术平均不小于这2个正数的几何平均.

接着教师展示问题2：

(让学生独立思考、演算，教师巡视、指导，然后逐一请学生板书，展示过程.)

生6：方法1 由(a-b)2≥0,得

a2+b2+2ab≥4ab,

即

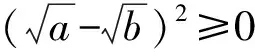
即

从而

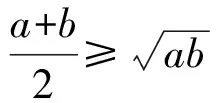
师：你是怎么想到的？

生6：方法1中不等式2边平方；方法2是作差，证明差大于等于0.

师：生6想到了平方与作差，这些方法非常重要.还有其他方法吗？

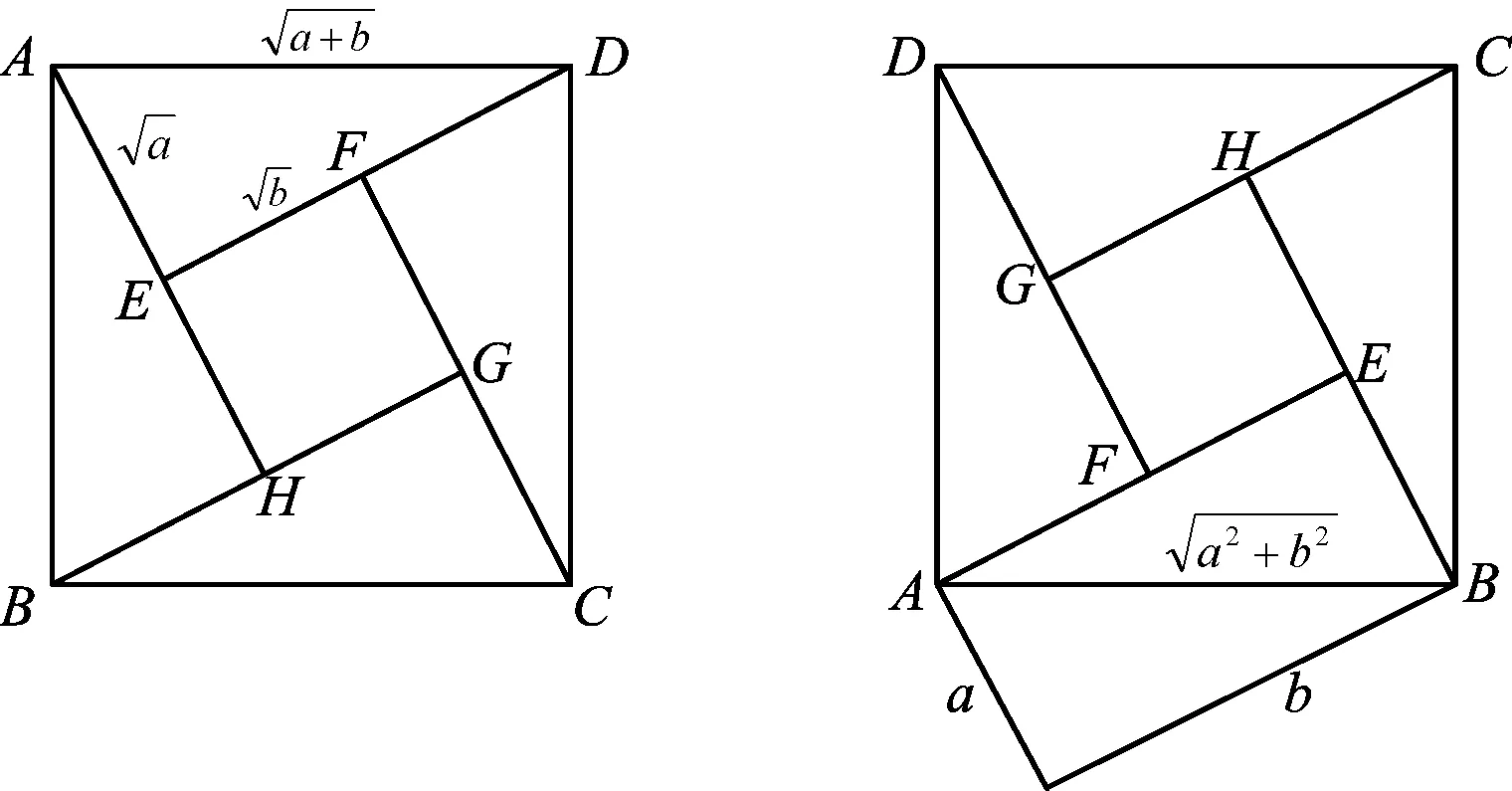
图1 图2

生9：如图2，S正方形ABCD=a2+b2≥4S△ABE=2ab.

(此时，下课铃响，学生10举手，经教师同意后板书自己的解法.)

(众生发出惊叹声.)

师：能想到反证法，很好.由于时间限制，还有许多方法没有时间展示，课后，请同学们把刚才的几种方法整理一下，相互交流，可能还会有第7、第8种证法.下节课我们再进行探讨.

2 课后反思

陶维林老师曾说：把时间还给学生，就是把原本属于学生的时间还给学生，把练习的时间还给学生，把活动的时间还给学生，把思考的时间还给学生……让他们来观察、来归纳、来概括、来探究、来交流、来参与举例、来参与定义、来参与再创造……，教师不要去占、去争、去抢，而是参与到学生的活动中去[1].在这堂课中，陶老师以实际行动践行了上述理念，设身处地把时间留给学生，有效地促进了学生数学地思考.具体体现在以下几个方面：

2.1 提出的问题少而精

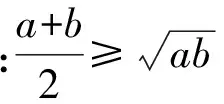
当代美国著名数学家哈尔莫斯曾说：“数学真正的组成部分应该是问题和解，问题才是数学的心脏，把问题作为数学教学的出发点，是现代数学教学的又一条原则.”然而在数学课堂中，部分教师缺乏对问题的深入研究，泛泛而问，表面上看，学生回答问题不断，师生互动频频，但由于提出的问题过于肤浅或琐碎而无法触及学生的思维深处.在这堂课里，陶老师结合学生前面已学的知识，从学生的最近发展区出发，只设计了2个问题，就将本课内容串起，而学生在问题驱动下能思、能说、能做，积极思维.由此可以看到，一个好的精炼的问题能“牵一发而动全身”，从而能留出尽可能多的时间让学生思考.

2.2 教师的话少而精

整堂课里，陶老师自己的话语不多，除了在2个概念(等差中项、等比中项)的辨析阶段，师生间开展了必要且有成效的交流外，其余时间只是说一些简短的提醒语、激励语，但给学生留出了总共近17分钟(整堂课课时40分钟)的独立思考、演算时间，很多时候课堂处于一种“静”的状态.上课一开始，师生互致问候后，教师多媒体展示问题1，但陶老师一言不发，在看到学生还没动笔时，陶老师说了几句提醒话，于是学生开始动手演算.该阶段共有近3分30秒的时间供学生思考、演算，然后在明确2个中项的大小比较要分情形讨论后，又给学生一定的演算时间，最后在证明不等式时，给了学生11分钟的思考、演算时间.同时，每当一个学生回答或解决了问题，总是叫答题者引导其余学生来评价，而不是首先由教师评价.

在当前的课堂教学中，常有这样的现象：教师提出问题后，没过几秒，马上就让学生回答，给学生思考的时间很短，甚至没有，导致学生的思考未及深处，其发言也往往不得要领.而此时，有的教师马上转问他人或开始新的提问；有的教师唯恐学生回答不完整或不正确，自己主动去补充或纠正答案.整堂课，总是充斥着教师个人的“噪音”，总是越俎代庖，从而使课堂教学成了教师的个人秀.显然，这样的教学只能使学生成为“熟练工”，但很难成为“思想者”.

古语云：“宁静致远.”教师要有意识地去精炼自己的语言，控制自己的“噪音”，把省下的时间留给学生思考，从而创造出数学教学的“静”界.我们的课堂不能仅仅是秩序井然，更要有民主与宽松的氛围.学生自己能学会的，尽量不教；学生应该想办法学会的，尽量少教；学生难以学会的，尽量去搭“脚手架”间接教.本堂课，陶老师有意地控制自己的讲授时间，很多时候一言不发，只在关键处作些追问与接话，而学生在这种时而宁静、时而热烈的和谐氛围中思维被激活、智慧在放飞，我们真切地感受到的是一堂如沐春风般的、富有生命力的高效课堂.

2.3 教师的板书少而精

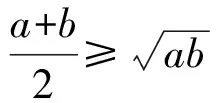
目前，高中数学课堂上还存在着教师讲得过多、写得过多的问题，部分教师对于学生课堂板演环节的必要性认识不足.在课堂上，我们常能看到：教师边讲边写，从黑板左上角写到右下角，满黑板都是个人的杰作，完全剥夺了学生板演的时间和空间，还自鸣得意.实际上，教师的板演突出的是讲授和示范，但如果只有教师的板演，学生则只能永远被动地接受，不利于调动学生学习的积极性和主动性.而通过让学生板演，则能改变以上弊端，弥补教师板演的不足.将学生的不同思路和念头展示出来，应视为一种思想与精神的交流和享受，从而让学生亲历成功所带来的认可与肯定，进一步强化其积极的自我评价.

诗人陆游说：“纸上得来终觉浅，绝知此事要躬行.”通过板演，就是要给学生搭起一个可以“躬行”的舞台，让学生在这个舞台上说出自己的想法，秀出自己的精彩，充分激发、揭示学生的思维活动，培养学生的课堂参与意识，从而进一步调动学生的学习积极性和主动性.本堂课，陶老师自己写得很少，而把时间、空间毫不吝啬地留给学生，于是就有了学生6种证法的精彩展示，从而给课堂带来了一波又一波的高潮.

章建跃曾指出：“数学教师区别于数学家，关键是他能在自己理解好数学的前提下，对数学知识做出符合学生认知水平的解释，使静态的、结果性的现成知识转化为生动的、易于被学生理解的形式.”[2]德国数学家第斯多惠认为：“教育的艺术不在于传授知识和本领，而在于激励、唤醒和鼓舞.”本堂课的设计，正顺应了这一导向，由于陶老师做到了对教材内容的本质把握和内在联系的深入理解，作出了与众不同的巧妙设计.综观整堂课，教师在往少而精努力——少而精的课堂问题驱动、少而精的教师表述、少而精的教师板书，而学生却在不停地思考，积极地交流，从而使教学有序、和谐、高效地展开，这种教学理念与实践值得我们去践行、去丰富.

[1] 陶维林.从“把时间还给学生”说起[J].数学通讯，2011(7)：1-4.

[2] 章建跃.数学学习与智慧发展[J].中学数学教学参考，2015(7)：4-10.

��2016-10-17；

2016-11-22

求莲萍(1983-)，女，浙江绍兴人，中学一级教师.研究方向：数学教育.

O122.3

A

1003-6407(2017)03-13-04