一堂从基本图形衍生的中考专题复习课*

●翁海芳 (仁爱中学 浙江宁波 315200)

一堂从基本图形衍生的中考专题复习课*

●翁海芳 (仁爱中学 浙江宁波 315200)

通过基本图形，层层推进，最终衍生为中考压轴题，引导学生在不断解决问题、不断收获成功的喜悦中，克服解题障碍，建立解题模型，提高能力素质.文章全程记录了一堂从基本图形衍生的中考专题复习课，课后反响较好.

中考复习课；基本图形；压轴题；衍生；建模

中考数学总复习是初中学生进行系统学习的最后阶段，复习效果将直接影响学生对数学知识的掌握程度.如何把复习课上得既生动活泼又务实高效，是每一位教师都必须深入研究的课题.现将笔者执教的一堂复习课介绍如下，供同行参考.

1 解决问题的3个步骤

第1步 提出问题，提炼基本模型

问题1 如图1，给你一个锐角△ABC和一条直线MN，你能用直线MN去截边BA与CA(或其延长线)，使截得的三角形与原三角形相似吗？

图1

学生在解决的过程中，发现直线MN所截的三角形有以下2种类型：

第1种可归结为“A”型(如图2～4所示)：

图2 图3 图4

第2种可归结为“X”型(如图5～6所示)：

图5 图6

以平行作为基本条件，以图2和图5作为基本图形，作进一步的构造设计.

第2步 设计问题，构造基本模型

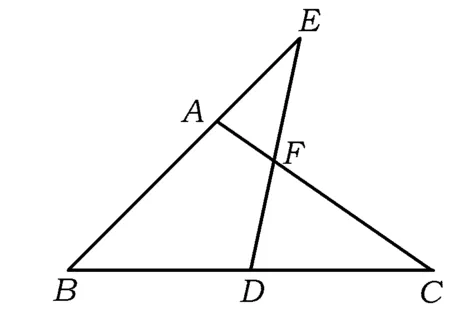
图7

问题2 如图7，若D为BC的中点，ED交AC于点F，且FC∶FA=3，求BA∶AE的值.

教师先让学生独立思考，然后让考虑成熟的学生上黑板板演.在课堂巡视中教师发现：除小部分学生不敢尝试添辅助线外，很多学生过点F或点A作平行线，也有一些学生过中点D作平行线.最终学生共想出6种添辅助线的方法，其中过点A,D,F各有2种添法.但没有一个学生想到过点B,E,C也可作辅助线.最后在教师的引导下，归纳总结得出结论：过图7中的每个点都有2种不同的平行线添法(如图8～13所示)：

图8 图9

图10 图11

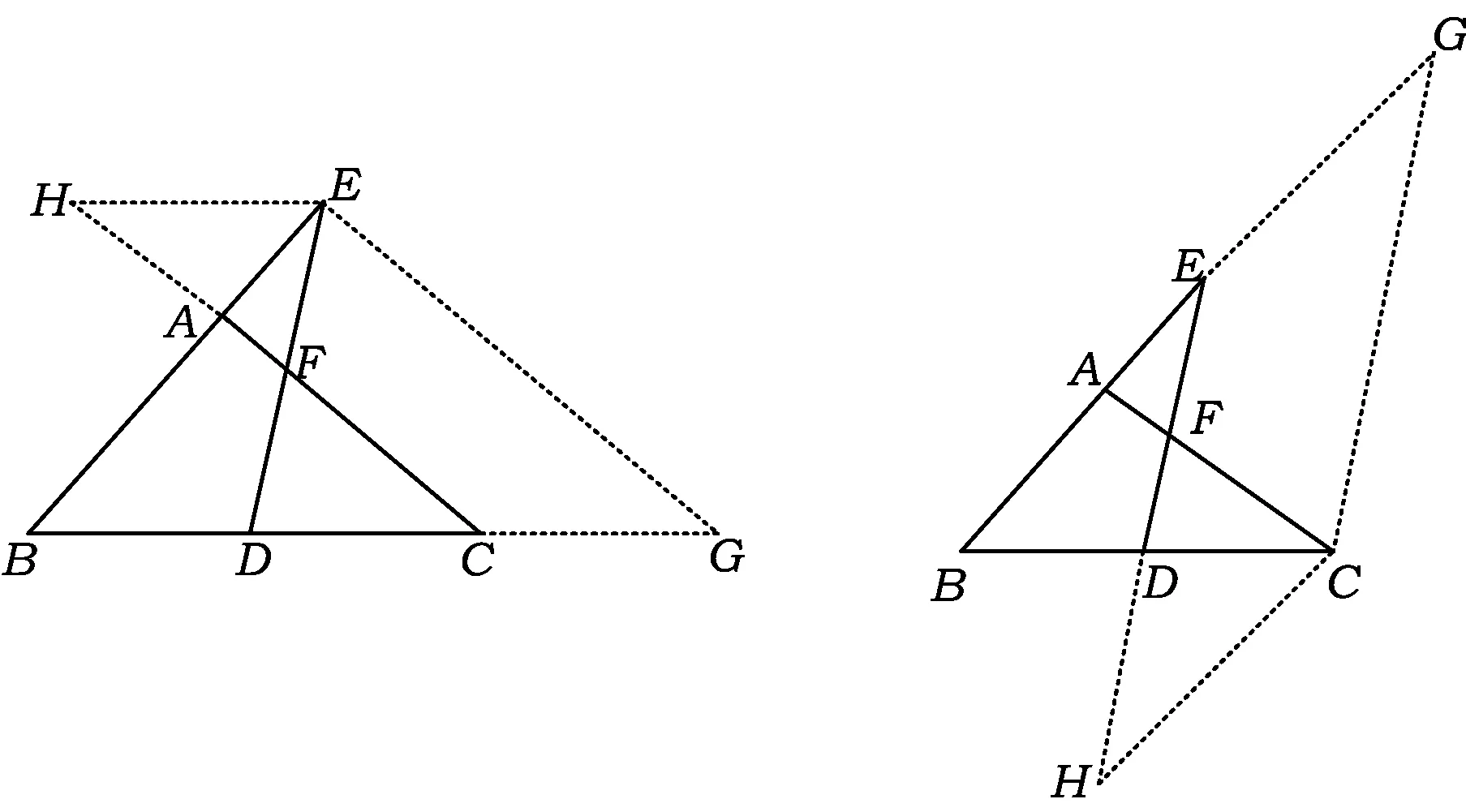
图12 图13

12种不同的辅助线添法相应有12种解答过程，从解题中可以看出，解决此类问题的关键是作平行线，也就是构造图2或图5这2种基本图形.它不一定是一种基本图形的简单运用，更多的是2个或2个以上的A型或X型基本图形的综合运用.学生看着这12种不同的解法不禁感叹：“居然有这么多方法，为什么我一种也想不出呢？”主要原因还是不敢尝试，缺乏面对困难勇于探索的精神.

第3步 拓展提升，强化学生的获得感

将问题2中的基本图形顺时针旋转90°，过2条相交线段的4个顶点作外接圆，再把外面的图形补全为一个直角三角形.学生们惊喜地发现:这正是2015年浙江省宁波市中考压轴题中的图形(如图14).本节课演变至此，学生的获得感和成就感油然而生，许多学生对解决平时望而生畏的中考压轴题更加有信心了.

问题3 如图14，在Rt△OAB中，M是斜边AB的中点,以OM为直径的⊙P分别交线段OA，OB于点C，D，交线段AB于点E，联结DE交OM于点K.若OK∶MK=3，求∠OBA的度数.

图14 图15

方法1 “X”型辅助线

如图15，联结DP，DM，易证DP∥BA，由△DKP≌△EMK，得DK=KE.根据垂径定理得OM⊥DE.

在Rt△DKP中，由DP=2KP，知

∠PDK=30°，

从而

∠DEB=30°，

于是

∠B=∠BOM=∠DEB=30°.

方法2 “X”型辅助线

如图16，联结DM，易证DM∥OA，可得DM∶OA=1∶2.延长DE交OA延长线于点H，联结OE，由△DMK∽△OKH，可证DM∶OH=1∶3，则有DM=AH.由△DME∽△HAE，可证ME=AE.又OE⊥AM，因此OA=OM.

在Rt△ODM中，由DM∶OM=DM∶OA=1∶2，知

∠DOM=30°，

从而

∠OBA=∠DOM=30°.

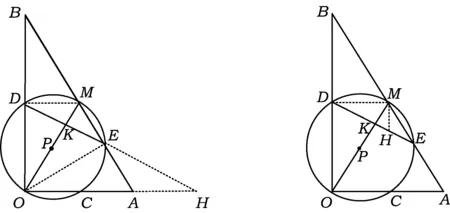
图16 图17

方法3 “X”型辅助线

如图17，过点M作MH∥BO交DE于点H.由△DKO∽△MKH，得

MH∶DO=MK∶OK=1∶3.

联结DM，易证DM∥OA，又点M是AB的中点，从而BD=DO，于是

MH∶DB=1∶3，

进而

EM∶MB=1∶2，

故点E为AM的中点，以下同方法2.

方法4 “A”型辅助线

如图18，过点K作KH∥OB交AB于点H，联结OE.由△MKH∽△MOB，得

MH∶MB=HK∶BO=1∶4，

易证D为OB的中点，从而

HK∶BD=1∶2.

由△EHK∽△EBD，得

EH∶EB=HK∶BD=1∶2.由以上关系可推得E为AM的中点，以下同方法2.

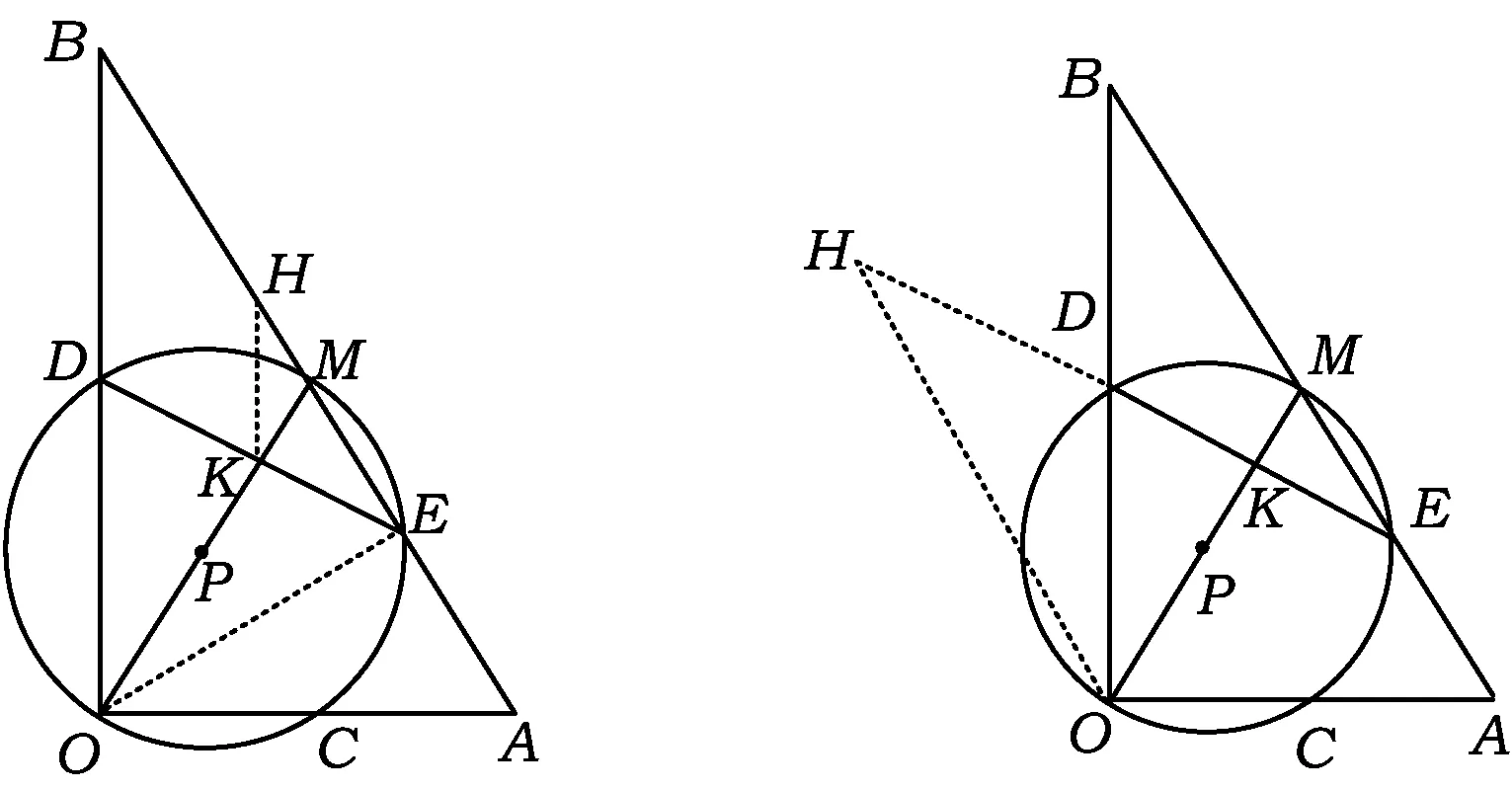
图18 图19

方法5 “X”型辅助线

如图19，过点O作AB的平行线与ED的延长线交于点H.由△MKE∽△OKH,得

ME∶OH=1∶3，

易证点D为BO的中点.由△BDE≌△ODH，知BE=HO，进一步可得E为AM的中点，以下同方法2.

��2016-10-13；

2016-11-16

翁海芳(1974-)，女，浙江宁波人，中学高级教师.研究方向：数学教育.

O123.1

A

1003-6407(2017)03-40-03