立体几何复习要点例析*

●孙军波 闫大贵 (温岭中学 浙江温岭 317500)

立体几何复习要点例析*

●孙军波 闫大贵 (温岭中学 浙江温岭 317500)

文章根据《2017年浙江高考考试说明(数学)》的知识要求和能力要求，结合近几年的浙江省数学高考命题，重点研究了“立体几何与空间向量”，归纳分析了一些经典问题：线面角、动态轨迹和翻折等问题，并整合一些经典试题供读者参考.

线面角；动态轨迹；翻折

1 知识内容

根据《2017年浙江高考考试说明(数学)》，立体几何的主要内容分以下几类：一是掌握三视图所表示的空间几何体，会计算柱、锥、台、球的表面积和体积，从宏观上了解几何体；二是理解空间点、线、面位置关系的定义，掌握可以作为推理依据的公理和定理，对几何体的位置关系进行论证；三是理解直线与平面所成角的概念，了解空间角的向量求法，对几何体的数量关系进行求解.

2 命题分析

纵观近几年的浙江省数学高考试卷，立体几何一直围绕考查学生的空间想象能力，要求学生能根据空间几何体的图形或几何形体的描述想象出相应空间形体(以三视图问题考查为主)，同时考查学生对几何形体进行分析、提取、概括来揭示其本质特征的能力，考查灵活运用几何形体的特性进行论证与求解的能力(以平行与垂直关系的判定和求空间角的问题为主)，往往还会涉及翻折等一些综合问题，考查学生的空间想象能力、逻辑思维推理的严密性和运算能力.

图1

3 典题剖析

考点1 线面角

例1 如图1，已知三棱锥D-ABC，记二面角C-AB-D的平面角是θ，直线DA与平面ABC所成角是θ1，直线DA与BC所成的角是θ2，则

A.θ≥θ1B.θ≤θ1C.θ≥θ2D.θ≤θ2

(2016年浙江省高中数学统测试题第9题)

分析 答案选A.本题可以用特殊值等多种方法解决.透过本题注意到线面角用直线和射影所成角来定义的合理性.根据最小角定理，斜线和它在平面内的射影所成角是这条斜线和这个平面内的任一条直线所成角中最小的角，它揭示了定义的合理性，考查了学生对概念的理解程度.二面角定义的合理性(唯一性)也是考查学生数学素养的有效途径.这样的考查在近几年的学考、高考试题中已多次出现.

图2

例2 如图2，某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB，某目标点P沿墙面的射击线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小.若AB=15 m，AC=25 m，∠BCM=30°，则tanθ的最大值______(仰角θ为直线AP与平面ABC所成角).

(2014年浙江省数学高考理科试题第17题)

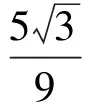
评注 虽然最小角定理不要求掌握，但是对于核心概念定义的合理性仍是值得探讨的一个问题，很好地考查了学生的数学素养.

图3

考点2 动态轨迹

例3 如图3，斜线段AB与平面α所成的角为60°，B为斜足，平面α上的动点P满足∠PAB=30°，则点P的轨迹是

( )

A.直线 B.抛物线

C.椭圆 D.双曲线的一支

(2015年浙江省数学高考文科试题第7题)

分析 立体几何动态轨迹问题的考查也是学生数学素养的考查(2008年浙江省数学高考理科试题第10题就是这样的题型)，这也是对圆锥曲线定义的深层次挖掘.古希腊数学家阿波罗尼奥斯采用平面切割圆锥的方法来研究这几种曲线，用纯几何方法将圆锥曲线的性质网罗殆尽.虽然课本是朝着解析法的方向发展，即通过坐标系得到圆锥曲线的方程，再用方程研究几何性质，以期达到抽象化的目标，不过阿波罗尼奥斯的想法仍然值得学习.学生可以观察如图4所示的4个图形，它们分别所对的曲线是圆、椭圆、双曲线和抛物线.

图4

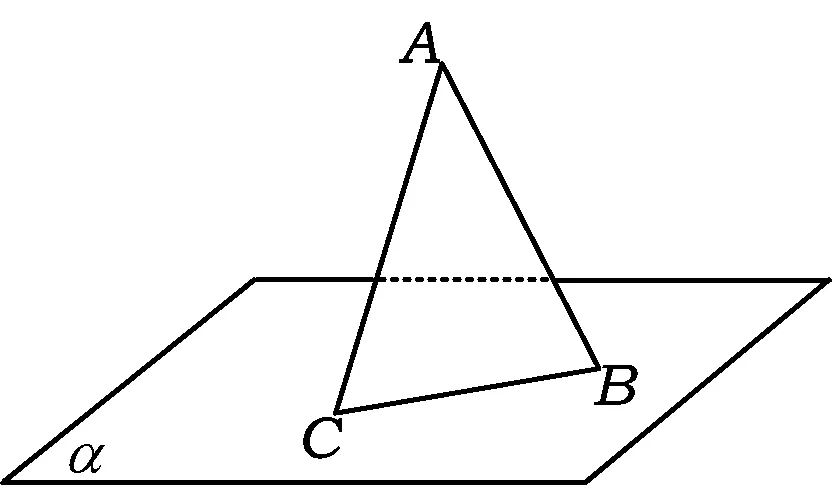
图5

例4 如图5，AB是平面α外固定的斜线段，B为斜足.若点C在平面α内运动，且∠CAB等于直线AB与平面α所成的角，则动点C的轨迹为

( )

A.圆 B.椭圆

C.双曲线 D.抛物线

分析 首先应关注∠CAB是个定角，由此确定点C在以AB为旋转轴的圆锥表面上;再考虑平面α和直线AB所成角等于∠CAB，以此确定平面平行于某条母线;最后确定其轨迹是抛物线.

评注 动态轨迹问题既考查了几何条件下的动点轨迹，又考查了基本几何体，是很好的命题点.

考点3 翻折问题

例5 如图6，在边长为1的正△ABC的边AB，AC上分别取点D，E，使沿线段DE折叠三角形时，顶点A正好落在边BC上，则AD长度的最小值为______.

(2008年浙江省高中数学竞赛试题第12题)

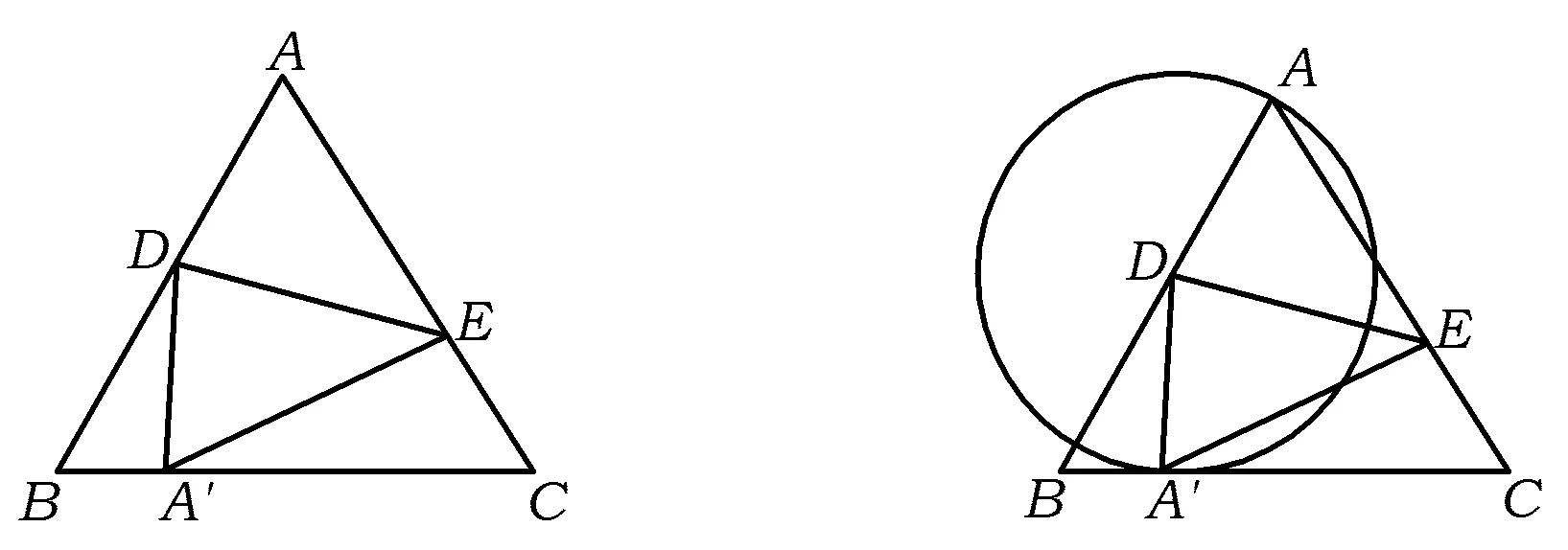
图6 图7

分析 折叠问题是立体几何中常见的问题，关键应抓住折叠前后的变量与不变量(角度、长度等)，然后根据相似三角形等构建等式求解，例如：

从而

解法2 如图7，点A,A′落在以D为圆心的圆上，当AD最短时圆与BC相切，从而

得

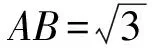
图8

分析 用向量来判断位置关系，运算量略为繁琐.在翻折问题中可以尝试抓住折叠中的运动量即二面角，不难发现随着二面角的变化，几何体随之发生改变.若翻折的角度确定，则几何体就确定.抓住翻折过程中的二面角就抓住了折叠的变化幅度.为叙述方便，如图9，不妨称直线BD为折痕线，称垂直于BD的直线AO为垂痕线.不难发现如下一些结论:

图9 图10

1)在翻折过程中，点A的轨迹是一个以O为圆心的圆;

2)在翻折过程中，点A在平面ABCD的射影都在直线AO上;

3)在翻折过程中，∠AOA′即为二面角A-BD-A′的平面角.

评注 解决翻折问题的核心在于抓住哪些是变量、哪些是不变量.在研究翻折问题中的轨迹、最值等一些问题，往往可以通过抓住“垂痕线”这个线索来解决.

考点4 三视图问题

例7 某几何体的三视图如图11所示,则此几何体的体积为

( )

图11

(2016年北京市数学高考理科试题第6题)

图12

分析 理解三视图与直观图的联系，并由三视图还原出简单几何体，是立体几何的基本要求，是高考的常考内 容，难点在于如何还原为空间几何体.在遇到复杂的几何体时，不妨考虑把它置于一个长方体中(如图12所示)，则更容易想象.该考点若出现在填空题的一题两空题型时，还应同时关注求表面积的相关问题.

考点5 证明和计算问题

1)求证：PD⊥平面PAB.

2)求直线PB与平面PCD所成角的正弦值.

(2016年北京市数学高考理科试题第17题)

图13 图14

分析 1)由面面垂直性质定理知AB⊥平面PAD，根据线面垂直性质定理可知AB⊥PD，再由线面垂直判定定理可知PD⊥平面PAB.

评注 空间垂直与平行的证明是考查学生逻辑推理的绝佳题型.引进空间向量后，如果空间几何体确定，特别是线面垂直关系明确后，无论证明或求解空间角，都可以转化为向量的运算.因此,在一般情况下，证明环节往往侧重逻辑推理，求解空间角时可以尝试多种方法求解.《2017年浙江高考考试说明(数学)》对空间向量的要求降低了一些，在选择题和填空题中出现的可能性减小，向量回归于工具角色的可能性较大.

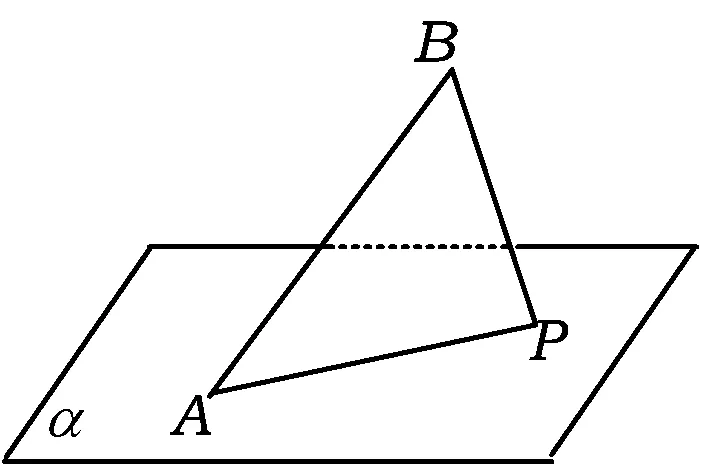
图15

4 精题集萃

1.如图15，AB是平面的一条斜线段，A为斜足，若点P在平面α内运动使得∠ABP=60°，则动点P的轨迹不可能是

( )

A.圆 B.椭圆

C.双曲线的一支 D.抛物线

2.如图16，在菱形ABCD中，∠BAD=60°，线段AD，BD的中点分别为E，F.现将△ABD沿对角线BD翻折，则异面直线BE与CF所成角的取值范围是

( )

图16

图17

3.如图17，已知△ABC，CD为∠ACB的角平分线，沿直线CD将△ACD翻折成△A′CD，所成二面角A′-CD-B的平面角为θ，则

( )

A.∠A′DB≤θ,∠A′CB≤θ

B.∠A′DB≤θ,∠A′CB≥θ

C.∠A′DB≥θ,∠A′CB≤θ

D.∠A′DB≥θ,∠A′CB≥θ

4.如图18，已知在矩形ABCD中，AB=2，AD=5，E在线段AD上，且AE=1，F为线段BC上一动点，现沿EF将四边形AEFB折成四边形A′EFB′，使得平面A′EFB′⊥平面CDEF.若点B′在面CDEF上的射影为H，则点H轨迹的长度为______.

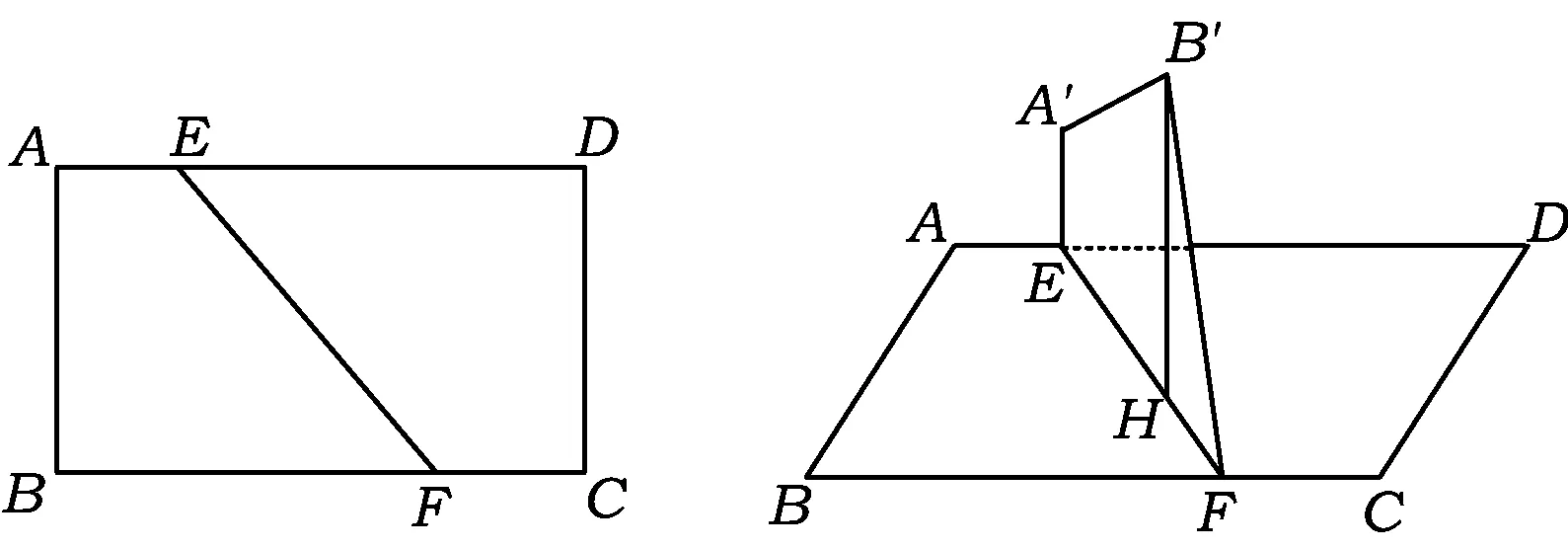
图18

5.某几何体的三视图如图19所示，其中侧视图和俯视图都是边长为2的正方形，则该几何体的体积为______，表面积为______.

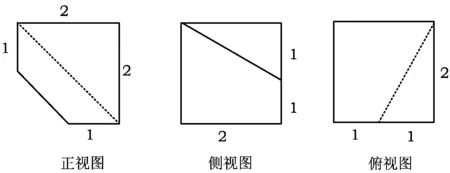
图19

6.已知点P,Q分别为正四面体A-BCD棱AB,BC上的动点(不包括端点)，则直线PQ与底面BCD所成线面角正弦值的最大值为______.

7.如图20，正四面体A-BCD的棱CD在平面α上，E为棱BC的中点.当正四面体A-BCD绕CD旋转时，直线AE与平面α所成最大角的正弦值为______.

图20 图21

8.如图21，已知在正三棱柱ABCD-A1B1C1中(底面是正三角形,侧棱垂直于底面)，AA1=AB，D为线段AC上的动点(包括端点).

1)若AB1∥平面BDC1，试确定点D的位置；

2)求直线AB1与平面BDC1所成角的正弦值的取值范围.

图22

1)求证:PO⊥平面ABCD；

2)求直线AP与平面PBC所成角的正弦值.

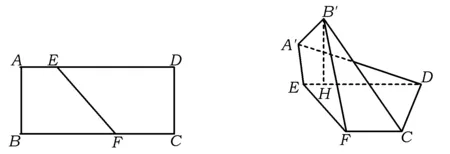
图23

10.如图23，已知在矩形ABCD中，AB=2，AD=5，点E，F分别在AD，BC上，且AE=1，BF=3.沿EF将四边形AEFB折成四边形A′EFB′，使点B′在平面CDEF上的射影H在直线DE上.

1)求证:A′D∥平面B′FC;

2)求直线B′H与平面A′ED所成角的大小.

参 考 答 案

1.A 2.C 3.C

8.解 1)联结B1C，交BC1于点E，联结DE，则平面BDC1∩平面AB1C=DE.因为AB1∥平面BDC1，所以AB1∥DE.又E是B1C的中点，故D是AC的中点.

图24

2)取AC的中点O,建立如图24所示的空间直角坐标系.不妨设AA1=AB=2，D(x,0,0),其中-1≤x≤1,则

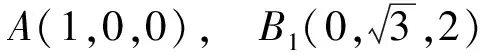
从而平面BDC1的法向量为

9.1)证明 由题意，在菱形ABCD中，BD⊥AC，因为平面PAC⊥平面ABCD，BD⊂平面ABCD，所以BD⊥平面PAC，从而BD⊥PO.

PO2+AO2=4=PA2，

于是

AO⊥PO.

又因为BD∩AO=O，所以PO⊥平面ABCD.

图25

于是

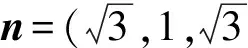
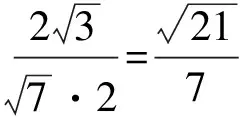
10.1)证明 因为翻折后A′E∥B′F，且A′E⊄平面B′FC，而B′F⊂平面B′FC，所以A′E∥平面B′FC.同理可得DE∥平面B′FC,从而平面A′DE∥平面B′FC，于是A′D∥平面B′FC.

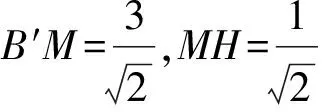
图26 图27

如图27，作HN⊥CF于点N，因为B′H⊥CF，所以CF⊥平面B′HN，从而平面CFB′⊥平面B′HN，于是点H在平面CFB′上的射影在B′N上，故∠NB′H即为所求角.在Rt△B′NH中，B′H=HN=2，从而∠NB′H=45°，即直线B′H与平面A′ED所成角为45°.

��2017-01-02；

2017-01-28

2016年浙江省台州市教科研课题

孙军波(1982-)，男，浙江温岭人，中学高级教师，教育硕士研究生.研究方向：数学教育.

O123.2

A

1003-6407(2017)03-35-05