“平面向量数量积在三角形中的应用”观摩的思考
——基于偶伟国老师的一节示范课*
●仝 建 (南京市大厂高级中学 江苏南京 210044)
“平面向量数量积在三角形中的应用”观摩的思考
——基于偶伟国老师的一节示范课*
●仝 建 (南京市大厂高级中学 江苏南京 210044)
基于偶伟国老师执教的一节示范课“平面向量数量积在三角形中的应用”,探究高效课堂形成的原因,提出高效课堂需注意留白的艺术、善用变式、营造积极心理场、注意“过渡”的设计、敢于放手.文章指出提高课堂实效,教师必须苦练“内功”,不断提高自身对数学学科、所教学生、教学艺术的理解水平.
数量积;三角形;示范课;高效课堂;原因分析
1 背景
2015年12月,江苏省苏州市第十中学举行的江苏省“师陶杯”颁奖会上,省特级教师偶伟国以“平面向量数量积在三角形中的应用”为题上了一节示范课,授课对象为该校某高一班级学生.笔者有幸到现场学习了这节课,感触颇深,收益良多.在偶老师的课堂上,学生情绪愉快,思考积极,教师引导合理、高效.课后通过学生访谈、反复学习偶老师这节课的教学录像,发现偶老师高效课堂形成的原因,并谈谈自己的几点思考.
2 教学实录
2.1 知识回顾
师:今天我们要用平面向量数量积解决三角形中的问题.数量积大家熟悉吧?
生(众):熟悉.
师:能把数量积的计算公式说一下吗?
生(众):a·b=|a|·|b|cosθ.
师(板书,并和学生一起说出公式):这里的θ是什么?
生(众):2个向量a与b的夹角.
师:夹角要注意什么?
生(众):共起点.
师:2个向量要共一个起点,2个向量夹角的范围知道吗?
生(众):[0,π).
师:数量积还有其他公式吗?
生(个别):没了.
师:假如把向量a的坐标记成(x1,y1),把向量b的坐标记成(x2,y2),还可以得到什么公式?
生(众):a·b=x1x2+y1y2.
评注 偶教师开门见山地直接提出研究课题,一句“数量积大家熟悉吧”唤起了全体学生的对课题的注意.从学生熟悉的内容(数量积计算公式)出发带动全体学生回顾基础知识,使每一个学生都能走进课堂,同时不留痕迹地指出学生在知识理解上的易错点——向量的夹角要使2个向量共起点.同时注意到:偶老师在课的开始阶段,多是“口语化”的交流,看似零碎,但师生交流的氛围好,学生能积极愉快地参与.笔者认为在课的开始阶段,“口语化”应多于“书面化”表达,这样更容易拉近师生的距离,把学生的注意力吸引到课堂中来.相反地,若一节课开始阶段,“书面化”表达过浓,则会导致师生无法共鸣,学生的思维难以被激活,从而可能导致师生在不同“频道”交流的尴尬现象.当然,教师要根据学生的情况作好“口语化”与“书面化”的平衡.
师:一个是跟向量模及夹角有关,一个是与坐标有关.同学们,你们前面用向量的数量积解决了什么问题?
生(个别):没解决什么问题,解决了数学问题.
师:解决了数学问题,看来老师问的问题不太好.大家看看数量积的公式跟什么有关?
生(众):跟角有关,跟模有关.
评注 偶老师说“看来老师问的问题不太好”,坦诚地在学生面前指出自己提问不好,把学生的不正确回答归因到自己身上,这样可以有效减少学生由于担心答错问题而产生的不敢回答问题、不敢展示自己想法的现象,有助于学生积极、主动地思考.接着,偶老师马上又修改了自己的问题“数量积的公式跟什么有关”,为学生思考指出了更加明确的方向.通过由远及近的问题,激活了学生的思维,并及时根据学生情况,调整问题的开放度.这当然不是偶老师的问题不好,而是教学艺术和智慧的体现.
师:通过向量的数量积可以研究向量的模、向量的夹角.当然,它还可以研究其他的内容.今天这堂课,我们用向量的数量积研究与三角形有关的问题.
2.2 例题评析

图1
教师用PPT投影并读题如下:

师(见没有学生抢答):口算不行了吧?大家算算看,困难来了.
(学生们开始安静思考、计算, 教师在黑板上画出△ABC.)

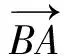

(教师根据生1的回答进行板书.)
生(众):转化.
生(众):基底.
师:同学们说得很好!
师:这个三角形是确定的吗?
生(众):是的,2条边夹1个角.
师:你能把这条边AB算出来吗?
(学生安静思考片刻后,教师提醒有困难的学生可以一起讨论.)
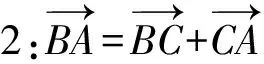
师:设想一下,能算吗?
生(众):可以,接下来拆开.
师:生2的想法是把一个向量转化为一组基底向量,最后通过平方的办法转化为长度.这个想法好不好?
生(鼓掌):好!
师:还有其他不同的想法吗?
(教师注意到学生的表情,示意一位学生回答.)
生3:过点A作AH⊥BC,交BC的延长线于点H,在Rt△ABH中,即可解得.
师(结合黑板上的图形):这就是“化斜为直”,用初中的知识就能解决了,但初中肯定没有向量的方法.大家看,向量很奇特吧,现在△ABC的3条边都是确定的.在这道题的条件下,你能提出其他问题吗?
生4:求∠B的大小可以通过∠B的余弦值求得.
(其他学生提出的问题此处从略.)
评注 波利亚给出解题的4个步骤:理解题意,拟定计划,执行计划,回顾[1]. 偶老师的教学中,特别重视解题后的回顾,这恰是不少教师在解题教学中容易忽视的地方.在生1解答之后,马上引导学生总结出解题的策略(向量转化)及解题方法(基底法), 使例题的功能得以充分发挥,解题方法得以固化. 通过追问“求边AB的长”,巩固例题教学形成的成果,同时也充分展示学生的不同想法,在通法(基底法)和巧法(化斜为直)中达到平衡.
2.3 变式练习
师:已知三角形的2条边和它们的夹角,借助向量可以求出第3条边和其他的2个角.
再看下面的问题(PPT展示变式1):


师(点评后):这3个数量积在等边三角形中是相等的.现在提这么一个问题:假如这3个数量积都相等,这个三角形是不是等边三角形呢?
PPT投影变式2:
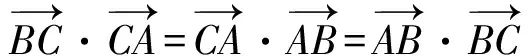
(学生们安静思考.)
生6:考虑到向量数量积的几何意义与投影有关.作BT⊥AC,垂足为T,则
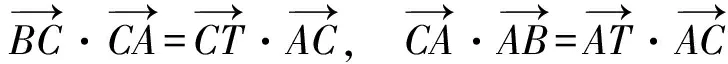
从而


(师板书并对该学生的说的式子用数量积进行解释).
师:用向量投影概念进行快速处理,太棒了!
(学生自发鼓掌,其他学生对变式2的回答此处从略.)
师:将变式2中的问题反过来,看下面的问题.
PPT展示变式3:

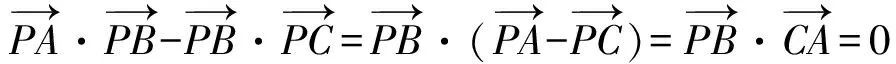
(教师板书并画图说明点P是△ABC的垂心,即3条高线的交点.)
师:三角形除了垂心,还有重心(3条中线的交点)、外心(3条中垂线的交点)、内心(3个内角平分线的交点),它们都与向量有相应的关系.请感兴趣的同学课后研究.下面我们看2道练习题.
2.4 感受高考

A.|b|=1 B.a⊥b

(2015年安徽省数学高考理科试题第8题)
(2015年福建省数学高考理科试题第9题)
(学生解答及教师评讲过程从略.)
评注 “如何保证课堂教学的后半段,学生也能思维活跃、不知疲倦地积极参与”是不少一线教师困惑的问题.注意到偶老师设计的例1特殊化就是变式1,通过调换变式1中的条件和结论得到变式2,变式3是变式2的一个反问题,这是一串紧密联系的问题组合,吸引学生不断深入下去,使学生的思考更加深入. 2道练习题是当年的高考题,对学生来说颇具新鲜感,有想试一试、挑战一下的冲动. 精心选择的问题加上教师充满激情的讲解与引导,使得学生在本节课的后半段也一直处在智力振奋的状态.
2.5 回顾总结
(此处从略.)
3 课后的访谈
课后笔者对部分学生进行简单访谈,并参与了偶老师对这节课的座谈会.
3.1 学生访谈
课后笔者随机对上课的学生进行访谈.
笔者:你对这节课的总体感受如何?
生1:感觉时间过得特别快,很开心.
生2:后面的问题很“烧脑子”,有意思.
笔者:你对老师的总体感受如何?
生3:老师上课很有趣,听他的课很愉快.
生4:这位老师上课我肯定不会睡觉的,他的课很有意思.
3.2 偶老师谈本节课课题的确定
偶老师在课后的交流中谈到:“一开始接到的课题是‘平面向量数量积的应用’,题很大,可以围绕向量的数量积、求模、求夹角这3个方面铺得很开,但容易散,难以深入.因此我选择了‘平面向量数量积在三角形中的应用’,这个课题切口小,好深入. ”
4 几点思考
4.1 注意留白的艺术
“留白”起源于绘画艺术,在作品中留有空白,可以增加艺术美感和想象空间.在本节课中,偶老师为学生留足了思考的时间,学生有思考的余地.如变式问题提出后,总能出现学生安静思考的状态.有的问题(如变式3之后偶老师提到重心、外心、内心都与向量有相应的关系.请感兴趣的同学课后研究),不讲完,留一点,留给学生思考的空间,这个思考的时空可以是课上,也可以是课下.偶老师恰当使用“留白”的艺术,延展了课堂时空,增强了课堂实效.
4.2 善用变式教学
变式教学是指教师有目的、有计划地对命题进行合理地转化.教师通过不断变更问题中的非本质特征、变换问题中的条件或结论、转换问题的内容和形式等,但应保留问题中的本质因素,从而使学生掌握数学问题的本质属性.当下市场上的复习资料,大多会在例题后面给出一道或几道所谓的“变式”,但实际上多是同类问题的累加,并非真正的变式,甚至和例题只是形似,并无本质关系.
4.3 善于营造积极心理场
美国心理学家、拓扑心理学的创始人勒温认为:人就是一个场,人的心理现象具有空间的属性,人的心理活动也是在一种心理场或生活空间中发生的.也就是说,人的行为是由场决定的.心理场主要是由个体需要和他的心理环境相互作用的关系所构成[2].
本节课是借班上课,上课地点是学校的阶梯教室,后面还有不少听课教师.这种情况下,师生难免都会有些紧张.上课的一开始,偶老师通过 “拉家常”的一问群答式,营造轻松愉快的课堂氛围,后续其间有个别回答,有教师真诚的鼓励,也有委婉的批评和激将,又有学生对学生由衷的赞叹,还有教师的自我批评等等.这些都构成了师生积极愉快的心理场, 就像访谈时几位学生所说“时间过得快,很开心”“有趣、愉快、有意思”. 学生在这样的课堂环境中,思维更容易被激活, 参与更有深度,课堂效果更好.
4.4 注意“过渡”的设计,打造自然的课
一节课除了设计出各个教学环节,还要注意各个环节之间的“过渡”的设计,就像主持节目,要“串好词,连成线,构成一个整体”. 偶老师指出:“向量数量积可以研究模,可以研究夹角.当然,它还可以研究其他的内容.今天的这堂课,我们用向量的数量积研究与三角形有关的问题.”由此自然引入例题,实现了从数量积知识的回顾到例题讲评的过渡.例题评讲中的追问也是自然产生,例题和变式之间以及后面的反馈练习,环环相扣,层层递进,不同环节的转换都有好的“过渡语”. 各个环节之间“过渡”自然,使本节课成为有机整体,这也应是高效课堂的成因之一.
4.5 敢于放手源于学科功底深厚
经常有专家在评课中提到,要敢于放手,潜台词是教师放手还不够.是什么原因使得教师不敢放手呢?在笔者和其他教师的交流中发现:很多教师不是不知道放手的好处,而是缺少放手的底气,放开了,还能引导好学生吗?能解决课堂上学生提出的问题吗?能收得了场吗?
本节课偶老师基于学生,敢于放手.课堂上的不少问题是由学生自己提出来的,如“在例1的条件下,提出求∠B”等.大胆放手,自然有利于培养学生思维的灵活性和创造性.《孟子·尽心下》中说:“贤者以其昭昭,使人昭昭. ”我们无法交给别人自己没有的东西,同样地也无法教会别人自己不会的东西. 偶老师敢于放手,正是源于他深厚的学科功底,及由此产生的高度教学自信(包括偶老师对课题作了一定的修改),可谓是艺高人胆大. 章建跃博士认为:教学设计能力是教师专业水平和教学能力的关键,其本质是理解数学、理解学生、理解教学的水平和能力[3]. 可见要提高课堂实效,教师必须苦练“内功”,不断提高自身对数学学科、所教学生、教学艺术的理解水平.
5 结语
偶老师的这一节课基于数学的深刻理解和学情的精准把握,充分地展现了精湛的教学艺术.特级教师的特别之处在哪里?笔者认为在于教师对数学学科特别深刻的理解,是学科知识的行家里手;在于对学生的理解与尊重,在此基础上形成良好的教学方法和教学艺术,组织学生切实地做好了“数学地交流和互动”,并形成了自己的独特风格.
[1] 波利亚.怎样解题[M].上海:上海科技出版社,2007.
[2] 仝建. 高立意低实效之追因[J].中小学数学:高中版,2016(6):26-28.
[3] 章建跃.在“落实立德树人根本任务全面深化课程教学改革”中再立新功[J].中国数学教育:高中版,2015(1/2):3-5.
��2016-11-03;
2016-12-06
仝 建(1980-),男,安徽灵璧人,中学一级教师.研究方向:数学教育.
O123.1
A
1003-6407(2017)03-09-04

