绝对值三角不等式的基本模式及其应用*

●周顺钿 (杭州高级中学 浙江杭州 310003)

绝对值三角不等式的基本模式及其应用*

●周顺钿 (杭州高级中学 浙江杭州 310003)

文章对绝对值三角不等式的基本模式进行解析，并结合近几年浙江省数学高考、学考和竞赛试题，分析了该模式的解题功能，肯定了思维定势正迁移的积极作用.

绝对值三角不等式；2边夹逼；模式识别；思维定势.

静心细思近年来浙江省数学高考、学考和竞赛试题，对绝对值三角不等式这个基本模式的考查频率之高，令人印象深刻.尤其是2016年浙江省数学高考，选择、填空、解答这3种题型的压轴题，都能找到绝对值三角不等式的影子，几乎达到了登峰造极的地步.

1 绝对值三角不等式的基本模式

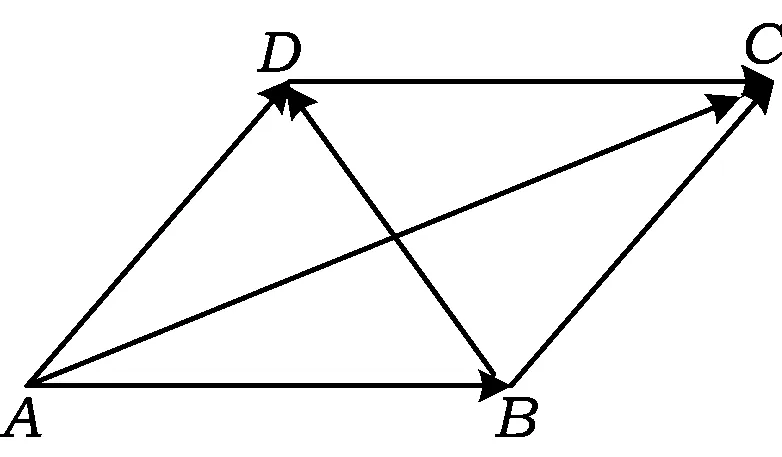
图1

在△ABC中，由“三角形两边之和大于第三边、两边之差小于第三边”可得

||a|-|b||<|a+b|<|a|+|b|，

对任意向量a,b，有不等式

||a|-|b||≤|a+b|≤|a|+|b|

成立，其中：

1)当a,b至少有1个为零向量时，有

|a+b|=|a|+|b|.

2)当a,b均为非零向量时，

①当a,b不共线时，

||a|-|b||<|a+b|<|a|+|b|；

②当a,b共线同向时，

|a+b|=|a|+|b|；

③当a,b共线反向时，

||a|-|b||=|a+b|<|a|+|b|.

评注 以-b替代b，有不等式||a|-|b||≤|a-b|≤|a|+|b|成立，它也可以由△ABD边的关系得到几何解释.

这就是向量形式下的绝对值三角不等式.特别地，当向量a,b的起点与坐标原点O重合、终点落在x轴上时，上述不等式就转化为实数形式下的绝对值三角不等式：

||a|-|b||≤|a±b|≤|a|+|b|.

其中等号成立的条件是：

①|a+b|=|a|+|b|⇔ab≥0；

②|a-b|=|a|+|b|⇔ab≤0；

③|a+b|=|a|-|b|⇔(a+b)b≤0；

④|a-b|=|a|-|b|⇔(a-b)b≥0.

推论 |a-c|≤|a-b|+|b-c|.

推广 |a1+a2+…+an|≤|a1|+|a2|+…+|an|.

一般情况下所讨论的向量空间(如实数空间、复数空间、Rn)都是很特殊的距离空间(线性赋范空间)，其中有一个很重要的性质叫做三角不等式，这正是绝对值不等式的一个缩影，这里的绝对值就是一个范数.

绝对值三角不等式是人教版《数学(选修4-5)》“不等式选讲”中的内容，《浙江省高考数学考试大纲》明确要求考生：掌握不等式||a|-|b||≤|a±b|≤|a|+|b|及其应用，它是数学解题的一个重要模式，也是浙江省数学高考的重要考点之一[1].

2 绝对值三角不等式的模式应用

2.1 基本模式的正用

( )

(2016年4月浙江省数学学考试题第18题)

分析 由题意：总存在x0∈[1,2]，使得f(x0)≥m成立，只需m≤f(x)max,x∈[1,2].记f(x)max=h(a,b),对任意的实数a,b，总存在x0∈[1,2]，使得f(x0)≥m成立，即m≤h(a,b)min，亦即

m≤(f(x)max)min,其中x∈[1,2].

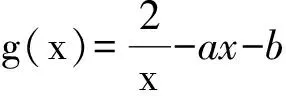
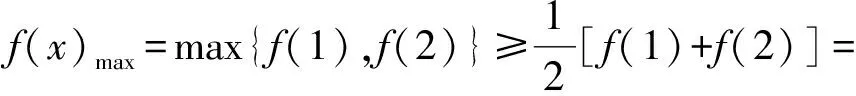
,当且仅当(2-a-b)+(1-2a-b)=0时，等号成立，因此

评注 对既有存在又有任意的函数问题，常常转化为相应函数的最值问题.

例2 已知函数f(x)=x2+ax+b(其中a,b∈R)，记M(a,b)是|f(x)|在区间[-1,1]上的最大值.

1)证明：当|a|≥2时，M(a,b)≥2；

2)当a,b满足M(a,b)≤2时，求|a|+|b|的最大值.

(2015年浙江省数学高考理科试题第18题)

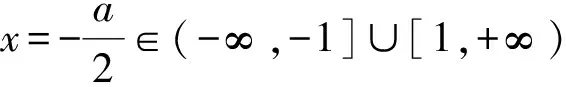
M(a,b)= max{|f(-1)|,|f(1)|}≥

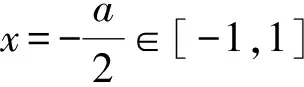
图2

即

而|a|+|b|=t>0在aOb坐标系内表示的图形是以O为中心、对角线与坐标轴重合的正方形(如图2所示)，由数形结合可知，当a=±2，b=-1时，|a|+|b|的最大值为3.

当ab≥0时，

|a|+|b|=|a+b|≤3；

当ab<0时，

|a|+|b|=|-a+b|≤3.

故当a=±2,b=-1时，|a|+|b|的最大值为3.

评注 特殊赋值、合理配凑并结合不等式的基本性质，是证明含绝对值不等式的行之有效的方法.

(2016年浙江省数学高考理科试题第15题)

a2+2a·b+b2≤6.

a2-2a·b+b2≤6.

(或从极化恒等式入手

|a+b|2+|a-b|2=2(|a|2+|b|2)=10，

评注 向量问题的核心是向量的加、减运算及其几何意义，以及数量积的几何意义.本题解法很多，但结合绝对值三角不等式求解，独辟蹊径，呈现了数学的和谐之美.

1)证明：|an|≥2n-1(|a1|-2)；

(2016年浙江省数学高考理科试题第20题)

分析 本题是以不等关系给出的递推数列.这是近年来罕见的，许多考生望题生畏，轻言放弃，实在是很可惜.

1)根据绝对值三角不等式，已知条件可以弱化为

即 |an+1|≥2|an|-2.

(1)

如果将式(1)中的不等号改为等号，那么数列{|an|}满足的递推关系就是我们熟知的一阶线性递推式，它可以往“等比、等差”2个方向进行转化.

等比方向：式(1)可进一步转化为

|an+1|-2≥2(|an|-2)，

依此传递可得

|an|-2|≥ 2(|an-1|-2)≥22(|an-2|-2)≥…≥

2n-1(|a1|-2),

于是

|an|>|an|-2≥2n-1(|a1|-2).

等差方向:式(1)的2边同除2n+1，得

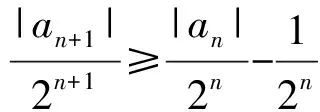
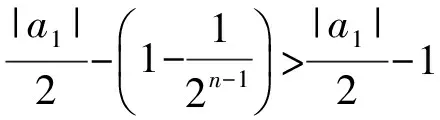
于是

|an|>2n-1(|a1|-2).

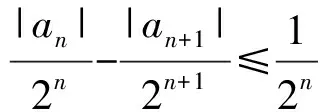
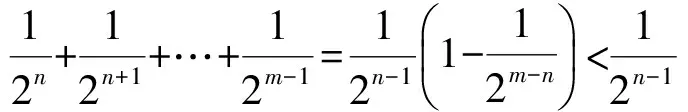
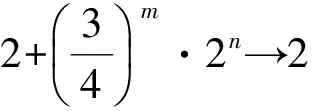
(或用反证法来说明.假设存在n0∈N*，使|an0|>2，则

于是

这与m的任意性矛盾.)

评注 本题有2个转化是很关键的：一是通过绝对值三角不等式将已知不等式弱化，化归为一阶线性递推关系；二是再将弱化的不等式化归为等比或等差累加这2个基本类型.第2)小题证明该数列项的有界性，这在《数学分析》课程里是比较常见的变形技巧，如今出现在2016年的数学高考中，可能又会形成日后新的热点.

3 取等条件的应用

分析 因为

1= sin2x-f(x)+f(x)+cos2x≤

|f(x)-sin2x|+|f(x)+cos2x|≤

所以

即

评注 “2边夹逼，化不等为相等”是解决本题的关键.

例6 设复数z1=(2-a)+(1-b)i,z2=(3+2a)+(2+3b)i,z3=(3-a)+(3-2b)i,其中a,b∈R.当|z1|+|z2|+|z3|取得最小值时，求3a+4b的值.

分析 观察易得

z1+z2+z3=8+6i，

于是

|z1|+|z2|+|z3|≥|z1+z2+z3|=10.

|z1|+|z2|+|z3|取得最小值当且仅当

解得

从而

3a+4b=12.

(2016年浙江省数学高考理科试题第8题)

分析 本题要确认哪个选项的条件能保证a，b，c是有界的.对于选择题，宜从特例入手，避免小题大做.

取a=b,c=-a2-a，则a的取值范围无界，故不合题意；

则a的取值范围无界，故不合题意；

下面证明选项D是正确的.

根据绝对值三角不等式

1≥|a2+b+c|+|a+b2-c|≥|(a2+b+c)+(a+b2-c)|，

当且仅当(a2+b+c)(a+b2-c)≥0时取到等号，

于是

a2+b+a+b2≤1，即

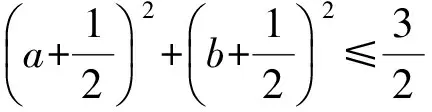
于是

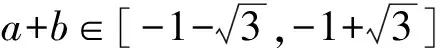
故

再由绝对值三角不等式

|c|-|a2+b|≤|a2+b+c|≤1,

得

|c|≤1+|a2+b|，

同理可得

|c|≤1+|a+b2|，

相加得2|c|≤2+|a2+b|+|a+b2|≤ 2+a2+b2+|a|+|b|.

若ab≥0，则

评注 解决数学问题应该从正确理解概念出发，抓住概念的本质，制定解题的策略.根据绝对值三角不等式，4个选项的条件依次可以弱化为

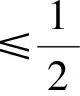
模式识别是重要的解题思想，绝对值三角不等式是数学解题的一个重要模式.在学习数学的过程中，所积累的知识经验经过加工，会得出有长久保存价值或基本重要性的典型结构与重要类型——模式，将其有意识地记忆下来，并作有目的地简单编码，当遇到一个新问题时，我们辨认它属于哪一类基本模式，联想起一个已经解决的问题，以此为索引，在记忆贮存中提取出相应的方法来加以解决，这就是模式识别的解题策略.

从思维的角度看，模式识别的解题策略体现了思维定势正迁移的积极作用.“遇新思陈，推陈出新”无非是为了在当前问题与头脑中已有的知识、经验之间建立联系，以诱发积极有用的思维定势.专家与普通人在解决问题时之所以会有区别，一个很重要的原因就在于专家能迅速找出贮存在大脑中的模式，作为检索问题解法的索引，从而大大减少搜寻的时间[2].

[1] 人民教育出版社课程教材研究所.普通高中课程标准实验教科书·数学(选修4-5)[M].北京：人民教育出版社，2005.

[2] 罗增儒.数学解题学引论[M].西安：陕西师范大学出版社，1997.

��2016-09-23；

2016-10-25

周顺钿(1965-)，男，浙江绍兴人，浙江省特级教师.研究方向：数学教育.

O122.3

A

1003-6407(2017)03-16-05