例谈高中数学中的定点问题研究

例谈高中数学中的定点问题研究

☉江苏省宝应县安宜高级中学 鲜黎

“定点”问题是解析几何试题中常见的一类题型，在近几年的高考或模拟试题中频繁出现，因为这类题型不仅体现了数学文化美，而且体现了哲学中动与静的辩证统一的关系，所以备受命题专家的青睐.下面笔者结合平时的教学实践，谈谈对这类定点问题的研究.

一、直线与圆的一类定点问题探究

高中数学直线方程和圆方程中有一类涉及定点和定值的问题.这类问题中一般都有变量或动点，但最终的数值或点却是一定的.解决这类问题，一般都用方程思想探得定值或定点，利用等式恒等的性质，可求出定点、定值.

例1如图1，已知圆M：x2+（y-2）2=1，Q是x轴上的动点，QA，QB分别切圆M于A，B两点.求证：直线AB恒过定点.

证法1：如图1，设A（x1，y1），B（x2，y2），Q（x0，0），

图1

x1x+（y1-2）y-2y1+3=0.同理x2x+（y2-2）y-2y2+3=0.

把Q（x0，0）代入上面两式得到x1x0-2y1+3=0，x2x0-2y2+ 3=0，

所以A（x1，y1），B（x2，y2）同时满足直线方程xx0-2y+ 3=0，即直线AB方程为xx0-2y+3=0，由x0的任意性得到定

证法2：设Q（x0，0），以MQ为直径的圆（x-0）（x-x0）+（y-2）（y-0）=0，即x2+y2-x0x-2y=0.圆M：x2+（y-2）2=1，即x2+y2-4y+3=0，两圆相减得到公共弦所在的直线方程x0x-2y+3=0，由的任意性得到定点（0，）.

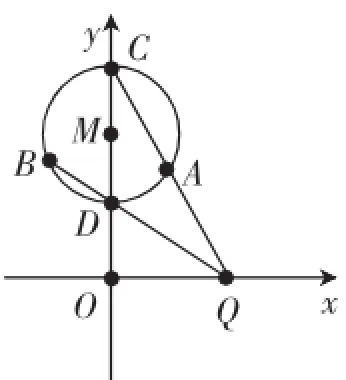
图2

证法3：直线AB也可以看成是以Q为圆心，MA或QB为半径的圆，和圆M的公共弦，证法如证法2.

变题1如例1中的圆M交y轴从上而下于C，D，如图2，连接QC，QD交圆M于A，B，证明：直线AB经过定点.

证明：设Q（x0，0），C（0，3），D（0，1）.

又因为Q关于原点的对称性，这个定点一定在y轴上，令x=0，得到

变题2若把圆M改为x2+（y-2）2=r2（0＜r＜2）.

（1）例1的定点又是什么？有什么发现？

（2）若把圆M改为x2+（y-b）2=r（20＜r＜b）呢？

11111

把Q（x0，0）代入上面直线方程得到x0x1-2y1-r2+4=0.

同理可以得到x0x2-2y2-r2+4=0.

所以A（x1，y1），B（x2，y）2同时满足直线方程x0x-2yr2+4=0.

由x0的任意性知

11111

把Q（x0，0）代入得到x0x1-by1-r2+b2=0.

同理可以得到x0x2-by2-r2+b2=0.

所以A（x1，y1），B（x2，y2）同时满足直线方程x0x-byr2+b2=0.

由x0的任意性知，

二、抛物线定点问题

当抛物线的弦所在直线过定点时，抛物线对称轴上一点与弦的两个端点形成的直线斜率或夹角平分有一定的定点性质，另外，在抛物线中还有其他几条定点问题，现例举说明几条结论.

结论1抛物线C：y2=2px与直线y=k（x-m）交于A，B两点，O是坐标原点，则k·k=-

OAOB

证明：设A（x1，y1），B（x2，y2），则

逆命题1抛物线C：y2=2px上两动点A，B，O为坐标原点，若·k=-，则直线AB过定点（m，0）.OB

结论2抛物线C：y2=2px与直线y=k（x-m）（其中m＞0）交于A，B两点，已知点E（-m，0），则∠AEB的平分线是x轴.

图3

12120，代入（*）得直线AE，BE的倾斜角互补，结合图3知，∠AEB的平分线是x轴.

逆命题2已知点E（-m，0）（其中m＞0），抛物线C：y2=2px上两动点A，B，若∠AEB的平分线是x轴，则直线AB过定点（m，0）.

结论3抛物线C：y2=2px与直线y=k（x-m）（其中m＜0）交于A，B两点，已知点E（-m，0），则∠AEB的平分线平行于y轴.

图4

12120，代入（*）得直线AE，BE的倾斜角互补，结合图4知，∠AEB的平分线平行于y轴.

逆命题3已知点E（m，0）（其中m＞0），抛物线C：y2= 2px上两动点A，B，若∠AEB的平分线平行于y轴，则直线直线AB过定点（-m，0）.

三、圆锥曲线中的定点问题

圆锥曲线中的定点问题是近几年高考中的热点，题型变化多端，灵活新颖.现举例说明圆锥曲线中定点问题的解题策略.

（1）求双曲线C的方程；

（2）过双曲线C的右焦点F作直线与双曲线左，右两支分别交于点A，B，点B在直线x＝上的射影是D，求证：直线AD过定点.

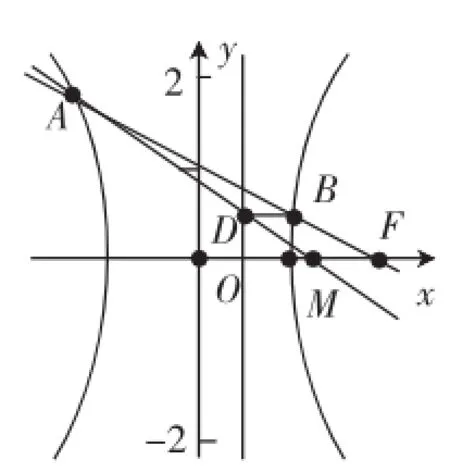
图5

解：（1）双曲线方程为x2-＝1（过程略）.

（3-k2）x2+4k2x-（4k2+3）＝0，Δ＝36（k2+1）＞0恒成立.

设A（x1，y1），B（x2，y2），则D

x1x2＝①设直线AD与x轴交于点M（t，0），只要证明t为常数即可.

证法1其思路很自然.亮点在于，根据双曲线C关于x轴对称，预设定点在x轴上，即D（t，0）.先将t表示为x1，y1，x2，y2的关系式；再消y1，y2转化为关于x1，x2的关系式；最后再消x1，x2转化为关于k的关系式，化简得结果，体现了化归与转化的思想.避免了复杂思路：将AD的方程设为y-变形得形如方程y-y0＝f（k）（x-x0），从而直线AD过定点（x0，y0）.

证法2，体现了整体消参的思想，计算过程明显简单.

下推广：

类比双曲线，可得椭圆与抛物线相关结论：

图6

结论3如图6，过抛物线焦点F的直线交抛物线于A，B两点，点B在抛物线准线上的射影为D，则直线AD必过抛物线顶点（定点）.（证明略）

几种圆锥曲线概念具有共生性，性质也有统一性，通过举一反三还可发现更多结论，如以上变式等.