关注教材旁白浸润数学文化提升核心素养*——由“数列”中的一个旁白引发的思考

☉重庆复旦中学 简榆新

关注教材旁白浸润数学文化提升核心素养*
——由“数列”中的一个旁白引发的思考

☉重庆复旦中学 黄益全

☉重庆复旦中学 简榆新

一、问题源起

1.关注教材旁白，拓展教学空间

在人教A版教材必修5［1］P29例1的旁边，教材编者给出了一个旁白“根据数列的前若干项写出数列的通项公式的形式唯一吗？请举例说明.”教材P32“阅读与思考”栏目又提供了“斐波那契数列”的阅读材料.数学教材中“旁白”“阅读与思考”等拓展栏目的素材常成为教师彰显自身教学风格的“自留地”，既拓展了教师的教学空间，又为学生自主学习搭建了平台，渗透着数学文化和数学思想，融理性思辨与实践智慧于一体，同时也是高考命题专家比较青睐的命题素材.可以说，教材“旁白”等拓展栏目及教材中的数学史料在积淀学生数学文化、提升学生核心素养方面起着相当重要的作用.教材没有太多的笔墨，但教师却不能没有思考.

2.浸润数学文化，提升核心素养

目前，新一轮课程改革正在积极酝酿中，中国基础教育课改正处于“再出发”阶段，与之相伴的则是核心素养的提出.数学课标修订组提出了六大数学核心素养：数学抽象、数学推理、数学建模、直观想象、数学运算、数据分析，它是五大基本能力（空间想象能力、抽象概括能力、推理论证能力、运算求解能力和数据处理能力）的延续和深化.学生核心素养的培养应当依托一定的载体，以构建“数学文化背景下的思维活动”为价值取向的教学设计是一种较好的选择［2］.在文化取向的教学设计中，我们的课堂教学不仅仅关注知识，还包括知识在内的整个文化.

二、旁白引发的思考

1.通项公式显魅力，深探妙赏育素养

数列的通项公式相当于函数的解析式，有了它，无异于抓住了数列的全貌，为我们计算数列的任意项和研究数列的性质提供了一个关键的抓手.那么“根据数列的前若干项写出数列的通项公式的形式唯一吗？”事实上，除等差数列、等比数列和一些项与序号n的函数关系明显的数列，可以直接凭归纳法写出通项公式外，一般有限数列通项公式的获取，其途径丰富多彩，过程妙趣横生.

例1数列｛an｝由1，-1，1，-1，…交替构成，其通项公式可表示为an=（-1）n+1，或an=cos（n+1）π，或an=sin或，也可表示为

以上构建过程均不失严谨，从不同角度体现出数学的抽象美.

例2斐波那契数列的前三项：1，1，2，我们可以设an=an2+bn+c，其图像过点（1，1），（2，1），（3，2），那么an的表达式不也是该数列的通项公式吗？［3］

再看该数列的前四项：1，1，2，3.在以上解法的基础上，可设前四项的通项公式为an=an3+bn2+cn+d，则有

显然，前后两个通项公式大相径庭，但却都满足前三项.实际上，斐波那契数列还有一个完整的通项公式：至此，有限数列通项公式不唯一的问题得以佐证.

这个问题引发了我们无限的遐想和追问：对于任意有限数列“a1，a2，…，an”，是否总可以构造一个次数至多是n-1次的多项式函数an=f（n），使其图象经过n个点A1（1，a1），A2（2，a2），…，An（n，an）呢？答案是肯定的.同时，我们还可以发现，在有限数列“a1，a2，…，an”之后任意增补一项an+1，都可得新数列的通项公式，该公式又同时是原数列“a1，a2，…，an”的通项公式，所以，数列“a1，a2，…，an”的通项公式随增项an+1的变化而变化，于是，可得数列的通项公式有无限多个.

以上构建多元方程组模型来确定有限数列通项公式的方法，对于缺乏线性代数基础的中学生而言，有较大的计算障碍.那么，能否规避障碍，让中学生在充满乐趣的心境中解决问题呢？答案是肯定的.事实上，早在18世纪，法国数学家拉格朗日就为中学生提供了一个可以掌握的、万能的插值公式［4］.

按照拉格朗日插值公式的构想，设an=f（1n）×（-1）+ f（2n）×π+f（3n）×10+f（4n）×，只需想法做到f（in）=，an的表达式即为所求.那么，f（in）如何构造呢？

事实上，只需取f1（

因此，对于任意k阶有限数列，只需构造an=f（n）=，其中

至此，任意有限数列的通项公式的存在性与构造性问题得以解决.其中，fi（n）（i，n=1，2，3，4，…，k）的构建，更展现了数列的韵律美，使运算过程充满了情趣.

2.数学文化入高考，核心素养润无声

事实上，高考试题中也常出现数列通项公式的背影，学生在解答高考试题的同时，对古典数学及数学文化进行了悄无声息的浸润.

例4［2008湖北卷理15题］观察下列等式：

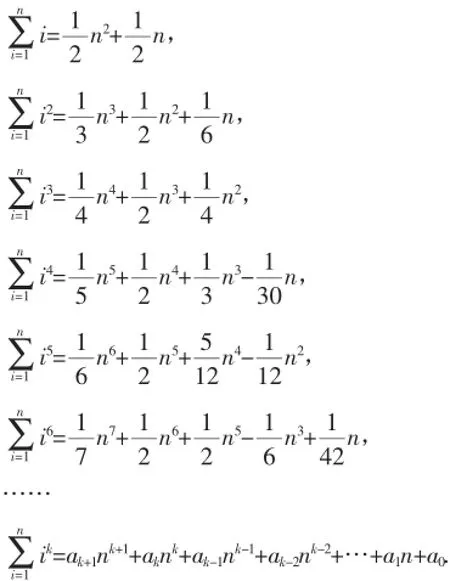
解析：由观察可知，当k≥2时，每一个式子的第三项的系数是成等差数列的，所以，第四项均为零，所以ak-2=0.

评注：此试题的命制背景是基于正整数幂和等式.设k，n为整数，n≥1，k≥1，记Sk（n）=1k+2k+3k+…+nk，规定S（0，k）=0，称S（n，k）=Sk（n）为前n个正整数的k次方幂和.正整数幂和的研究是一个古老而极具魅力的数论问题，它与G.Giuga猜想、伪素数、费马数、伯努利数等都有关系，长期吸引着古今中外众多杰出数学家如阿基米德、朱世杰、欧拉、陈景润等倾心研究.13+23+33+…+n3=（1+2+ 3+…+n）2是著名华裔数学家陶哲轩少年时期最钟爱的幂和恒等式.中国清代著名数学家李善兰先生也研究过幂和正整数，并于1859年在《垛积比类》一书中首次提出了“李善兰恒等式的组合公式”：该式驰名中外，自20世纪30年代以来，受到国际数学界的普遍关注和赞赏.

例5（2012湖北卷文17题）传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如下图所示的三角形数：

将三角形数1，3，6，10，记为数列｛an｝，将可被5整除的三角形数按从小到大的顺序组成一个新数列｛bn｝，可以推测：

（1）b2012是数列｛an｝中的第_____项；（2）b2k-1=______.（用k表示）

解析：由以上规律可知三角形数1，3，6，10，…，的一个通项公式为写出其若干项有：1，3，6，10，15，21，28，36，45，55，66，78，91，105，110，发现其中能被5整除的为10，15，45，55，105，110，故b1=a4，b2=a5，b3=a9，b4=a10，b5=a14，b6=a15.

故b2012=a2×1006=a5×1006=a5030，即b2012是数列｛an｝中的第5 030项.

评注：事实上，公元前6世纪，还没有纸，用小石子来研究数的性质，既方便又直观，也是认识数的一种有趣方法.英语中的“计算”（Calculation）一词来源于拉丁文“Calculus”，是小石子的意思.最早把正整数和几何图形联系在一起的是古希腊毕达哥拉斯学派，他们把数描绘成沙滩上的小石子，又按小石子所能排列的形状，把正整数与正三角形、正方形……等图形联系起来，将数分为三角形数、正方形数……这样一来，抽象的正整数就有了生动的形象，寻找它们之间的规律也就容易多了.以此为原形编制的高考试题在考查学生观察问题、分析问题、解决问题的能力及归纳推理能力、猜想能力的同时，也让学生感受古代数学家的智慧.真可谓“小石子中蕴藏大天地”！

例6（2013湖北卷理14题）古希腊毕达哥拉斯学派的数学家研究过各种多边形数.如三角形数1，3，6，10，…，第n个三角形数为记第n个k边形数为N（n，k）（k≥3），以下列出了部分k边形数中第n个数的表达式：三角形数

正方形数N（n，4）=n2，

六边形数N（n，6）=2n2-n，

……

可以推测N（n，k）的表达式，由此计算N（10，24）= _______.

评析：此例以“形数”知识为背景，有着深厚的文化底蕴，如三角平方数构成的数列的通项公式为fn=·另外斐波那契数列的通项公式为，这两个含有无理数的通项公式，给出的解却都是正整数，神奇之处如此一致，不得不令人叹服！

在前几年的高考自主命题中，湖北省对数学文化的考查可谓独树一帜，从教材正文、教材旁白、阅读与思考等拓展栏目，到传世名著、古典数学史料、数学猜想、历史名题等，都成为湖北省命制高考数学试题的素材，由此逐渐形成了“依托数学史料，嵌入数学名题，彰显数学文化”的鲜明特色.

人教A版高中数学教材非常关注对学生数学文化的熏陶和感染，在必修5中多次出现了古代数学家研究数学问题的文化背景，如P28毕达哥拉斯学派研究三角形数和正方形数，P30“谢宾斯基（Sieipinski）三角形”，P32“斐波那契数列”，P42“高斯求和”问题，P48以我国古代学者在《庄子.天下篇》中的一句话：“一尺之棰，日取其半，万世不竭.”来引入等比数列，P55以国际象棋起源的故事引入等比数列求和问题，P59中国古老智力游戏“九连环”等.例5、例6就取材于此，这类试题“巧妙地将数列问题融于其中，要求考生充分挖掘信息，根据图形规律归纳推理出数量关系.既合理引用了经典史料，又不刻意增加难度，同时对考生的‘数感’进行了有效的考查，让学生在数学史的背景中体会数学的文化价值.”［5］与此同时，学生的六大核心素养在悄无声息中得以提升.教师如能对教材中的这些内容加以关注，通过课堂教学和选修课加以拓展，则是培养学生核心素养的一种重要途径.

三、结束语

随着素质教育的深入推进和立德树人教育改革目标的实施，学生学科核心素养的培养已正式提上日程，数学文化也将渐入高中数学课堂.核心素养理念支撑下的数学教学应当是以知识教学为核心的文化教学，是数学文化背景下的思维活动，是孕育学生核心素养的重要载体之一.关注和培养学生核心素养的课堂，不应忽视教材的拓展性栏目.诚然，自新课程改革以来，课时紧张，高考压力增大是不言的事实.但对学生核心素养的浸润和培养更是我们中学数学教师不二的选择.在不断重视过程性教学和学科核心素养的今天，我们的课堂教学要对局部核心知识的学习、重要数学方法的体验、拓展栏目涉及的古典数学史料的追寻等数学学习过程以“慢”来浸润，需要有意拉长被压缩了的思维过程和数学发展历程来丰富学生发现、探索、体验的过程，提供文化背景，创建文化氛围，挖掘文化内涵，浸润文化根基，促使学生在思维的慢镜头和历史的长河中感知、体验数学及数学文化.教师可以通过开设选修课，以小专题形式对教材拓展栏目的内容加以深化、拓展，开阔学生视野，丰富学生的数学意识，增强数学文化的感染力和渗透力，为提升学生的学科核心素养做应有的努力.

1.人民教育出版社等.普通高中课程标准实验教科书（A版）：数学5（必修）［M］.北京：人民教育出版社，2007.

2.陈敏，吴宝莹.数学核心素养的培养——从教学过程的维度［J］.教育研究与评论.中学教育教学，2015（4）.

3.孙泰.数列好玩［J］.中学数学教学参考（上旬），2015（4）.

4.连春兴.一个可被中学生掌握的插值公式［J］.数学通报，1990（3）.

5.梅磊.题题充满数学味十年辛苦不寻常——十年高考数学湖北卷“亮点”题赏析［J］.中学数学（上），2014（1）.

*本文系重庆市教育科学“十二五”规划2015年度基础教育课程改革专项重点课题“人教版初高中数学课标教材中旁白的功能价值与教学应用研究”（课题批准号：2015-JC-041，课题负责人：黄益全）研究成果.