以“含参数不等式恒成立问题”为例谈高三复习策略

以“含参数不等式恒成立问题”为例谈高三复习策略

☉江苏省无锡市青山高级中学 陈波

高三复习是临门一脚，复习质量直接关系到学生高考的成败，尤其是二轮复习.笔者以“含参数的不等式恒成立问题”为例，笔者就如何有效复习谈几点思考.

一、宏观上对考点要有整体性的把握

二轮复习是针对考点的专题性复习，我们在实施复习课教学时，必须对考点有清晰、全面的认识，当然如何认识？是不是仅仅针对本省（江苏）高考题进行分析呢？显然这样是不够的，我们需要对全国各地的考题有一个系统的把握，考题是考试命题专家集中了群体智慧精心打磨直击考点的最佳问题，通过对高考真题的分析继而了解，这部分内容有哪些重要的题型，涉及哪些数学思想方法，继而接近专题的本质.

“含参数不等式恒成立问题”是近几年各地高考的一个热门题型，在解决这类问题的过程中涉及了“函数与方程”“化归与转化”“数形结合”“分类讨论”等数学思想，是考查学生对函数理解的重要题型.解决这类问题，主要是运用等价转化思想，把不熟悉不规范的、复杂的问题转化为熟悉规范甚至模式化、简单的问题.笔者认为，不等式恒成立问题的本质就是求最值问题.

二、微观上对数学方法有准确的拿捏

仅仅停留在宏观上是不够的，我们必须将问题和解决问题的方法呈现出来，在具体教学实践中可以给学生提供典型的例题和解析，借此引导学生对专题中涉及的问题和解决问题的方法进行归类、总结，唯有如此才能让学生明白：这部分内容考什么？怎么考？如何作答？有没有其他的解决办法？便于学生以后解决此类问题时可以很顺利地完成知识、方法的提取，准确的拿捏继而得分.

例如，笔者在复习课上和学生对于“恒成立问题”进行了如下的归类解析，在解析归纳中有方法的延伸和思维的提炼.

（一）直接构造函数解决

例1设函数f（x）=ln（1+x），g（x）=xf′（x），x≥0，其中f′（x）是f（x）的导函数.若f（x）≥ag（x）恒成立，求实数a的取值范围.（2014，陕西，理）

解：已知f（x）≥ag（x）恒成立，

当a≤1时，φ′（x）≥0（当且仅当x=0，a=1时等号成立），所以φ（x）在［0，+∞）上单调递增，

又φ（0）=0，所以φ′（x）≥0在［0，+∞）上恒成立，

当a＞1时，对x∈（0，a-1］，有φ（′x）＜0，

所以φ（x）在（0，a-1］上单调递减.

所以φ（a-1）＜φ（0）=0.

所以，当a＞1时，存在x＞0，使φ（x）＜0，

综上可知，a的取值范围是（-∞，1］.

方法拿捏：此题不等式两边都含有相同的变量x，且含有整体变量（x+1），所涉及的函数较简单，故考虑直接移项作差，构造函数，运用导数求最值问题.若不等式f（x）＞A在区间D上恒成立，则等价于在区间D上［f（x）］min＞A（或者f（x）的下界大于A）；若不等式f（x）＜B在区间D上恒成立，则等价于在区间D上［f（x）］max＜B（或者f（x）的上界小于B）.例如，含参数的一元二次不等式或含有指数、对数函数的恒成立问题，如果将不等式转化成函数或相应的方程，再通过求最值、特殊值和对称轴等性质可使问题顺利解决.

（二）利用参变分离解决

方法拿捏：参数分离是一种常见的方法，常常在题目中避免了很多分类讨论.学生在面对不等式恒成立问题时，首先就会想到参变量分离，但本题g（0）不存在会导致学生仅利用高中知识体系无法求出b的最小值.而且本题在学生解决问题后，应该进一步进行方法的牵引，帮助学生进行思维的扩散，促进新方法的生成.

（三）利用分类讨论解决

仍以例2为例说明：

方法拿捏：如何对参数进行分类是学生运用分类讨论思想解题时的一大难点，引导学生关注端点函数值是否为零以及导数的变号零点是分类的关键.此题当0＜c＜1时，零点不可解出，为讨论增加了难度.当然，学生在两种解法的对比过程中思维方法得到了进一步的提升.

（四）利用放缩法解决

（2）若不等式ax+x2++2（x+2）cosx≤4对x∈［0，1］恒成立，求实数a的取值范围.（2013，辽宁，文）

解：（1）（作差求导法）略.

（2）因为当x∈［0，1］时，ax+x2++2（x+2）cosx-4=

当a＞-2时，不等式ax+x2++2（x+2）cosx≤4对x∈［0，1］不恒成立.下面给出证明：

因为x∈［0，1］时，ax+x2++2（x+2）cosx-4 x∈［0，1］恒成立.

所以存在x0∈（0，1）满足

故当a＞-2时，ax+x2++2（x+2）cosx-4≤0对x∈［0，1］不恒成立.

综上，实数a的取值范围是（-∞，-2］.

方法拿捏：第（2）题中的不等式涉及了三角函数和多项式是一种复杂函数，让人感觉无从下手.第（1）题是证明不等式成立，为其作了很好的铺垫，也极易想到利用所证得的不等式去解决问题.对参数a进行分类讨论时，根据a不同的范围选择不同的不等式进行放缩，目的是把复杂的函数简化成一类函数.若不等式中涉及不只一类函数且是复杂函数，可考虑利用已知的不等式或函数的相关性质对其进行放缩，进而转化为简单函数或一类函数，化繁为简.

（五）利用数形结合的思想解决

例4若不等式（x-1）2＜logax在x∈（1，2）内恒成立，则实数a的取值范围为______.

解：设f1（x）=（x-1）2，f2（x）=logax，要使当x∈（1，2）时，不等式（x-1）2＜logax恒成立，只需f1（x）=（x-1）2在（1，2）上的图像在f2（x）=logax图像的下方即可.

当0＜a＜1时，显然不成立；当a＞1时，如图1所示，要使x∈（1，2）时，f1（x）=（x-1）2的图像在f2（x）=logax的图像下方，只需f1（2）≤f2（2），即（2-1）2≤loga2，loga2≥1，所以1＜a≤2，即实数a的取值范围是（1，2］.

方法拿捏：本题只适合用图像分析法解决，用参变分离或者转换为求函数的最值都很难进行.

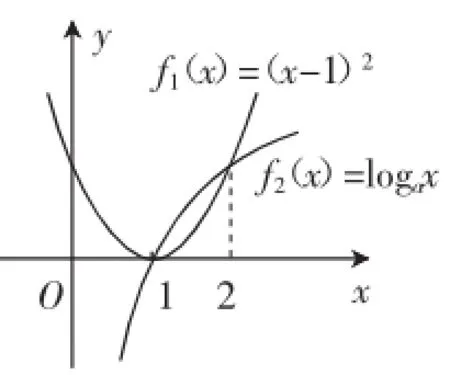
图1

三、自主总结与提升

我们的专题复习课不能仅仅只有解题，还应该有反思与总结，尤其是在完成了多道例题后，应该引导学生进行及时的总结，这样学生对该专题的认识才会更为深刻.

例如，含参数不等式恒成立问题的关键词是“恒”字，但也有其他意思相近的词，如“总”“始终”“都”等，解题时需要认真审题，在审题后能建立模型，得出恒成立问题.至于采用哪种求解策略，各有利弊，需要结合题目的具体特征.总之，我们应学会看透问题本质，提升思维与分析能力.