对一道课本例题的变式探究

安徽省宁国中学 (242300)

陈晓明

对一道课本例题的变式探究

安徽省宁国中学 (242300)

陈晓明

普通高中课程标准实验教科书《数学》选修2-1(人教A版)第70页例5：过抛物线焦点F的直线交抛物线于A，B两点，通过点A和抛物线顶点的直线交抛物线的准线于点D，求证：直线DB平行于抛物线的对称轴.

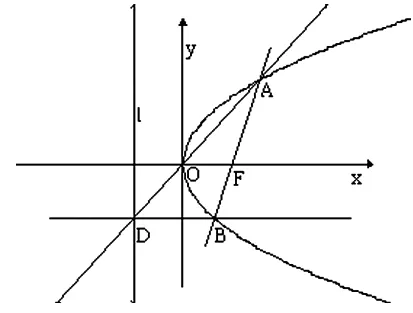
图1

在过去的教学中笔者直接讲解此例，发现绝大多数学生难以掌握，春去秋来，又是一届学生，我改变了教学方式.首先将此例具体化为特殊的抛物线y2=4x进行研究，然后推向一般即得例题结论，再进一步进行变式探究.收到了意想不到的效果！

改编例题：过抛物线y2=4x焦点F的直线交抛物线于A(x1,y1)，B(x2,y2)两点，通过点A和抛物线顶点的直线交抛物线的准线于点D，求证：直线BD∥x轴.

(为了证明此例，首先给出引例：过抛物线y2=2px焦点F的直线交抛物线于A(x1,y1)，B(x2,y2)两点，求证：y1y2=-p2.

课本中的证法有些繁，我给出改编例题的简便证法：

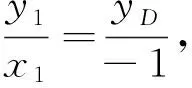
接下来再让学生把结论推向一般式y2=2px，学生很快证明了课本例5.我紧接着对例题进行变式，并让学生证明，然后把结论推向一般.

变式1过抛物线y2=4x焦点F的直线交抛物线于A(x1,y1)，B(x2,y2)两点，过B点作x轴平行线交准线于一点D.求证：A，O，D三点共线.

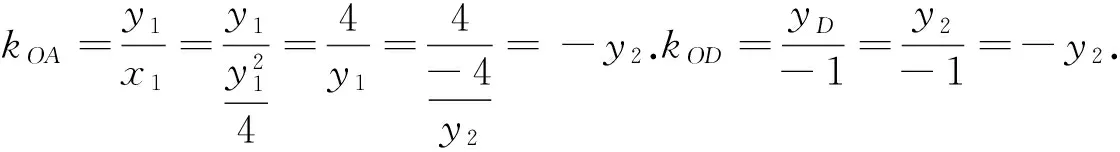
变式2过抛物线y2=4x焦点F的直线交抛物线于A(x1,y1)，B(x2,y2)两点，过B点作x轴平行线与AO延长线交于一点D.求证：D点在一条定直线上.

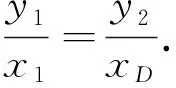
拓展1过点M(2,0)的直线交抛物线y2=4x于A(x1,y1)，B(x2,y2)两点，过点B作x轴平行线与AO延长线交于一点D.求证：D点在一条定直线上.

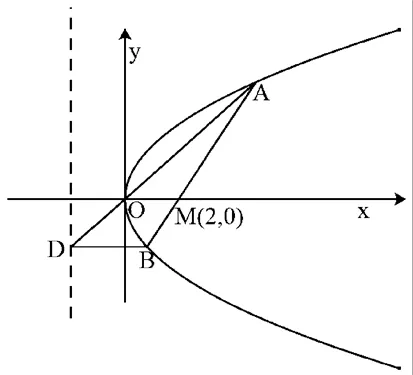
图2

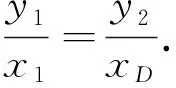
∴xD=-2.即D点在一条定直线x=-2上.

拓展2过点M(a,0)(a>0)的直线交抛物线y2=4x于A(x1,y1)，B(x2,y2)两点，过点B作x轴平行线与AO延长线交于一点D.求证：D点在一条定直线上.

同理可证定直线为x=-a.

试题链接:我们来看一下2014年江西高考题(文科第20题)：

如图3，已知抛物线C:x2=4y，过点M(0,2)任作一直线与C相交于A，B两点，过点B作y轴的平行线与直线AO相交于点D(O为坐标原点).

图3

(1)证明：动点D在定直线上；

(2)略.

变式3如图1，已知D为抛物线y2=4x准线上一点，抛物线焦点为F，过D作x轴平行线与抛物线交于一点B(x2,y2)，直线BF与DO延长线交于一点A(x1,y1)，求证：点A在抛物线上.

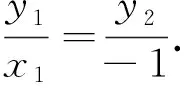
变式4如图1，已知D为抛物线y2=4x准线上一点，抛物线焦点为F，连结DO并延长与抛物线交于一点A(x1,y1)，过点D作x轴平行线与直线AF交于一点B(x2,y2).求证：点B在抛物线上.

证明略.

变式5如图1，已知D为抛物线y2=4x准线上一点，抛物线焦点为F，连结DO并延长与抛物线交于一点A(x1,y1)，过点D作x轴平行线与抛物线交于一点B(x2,y2).求证：A，F，B三点共线.

证明略.

反思与小结

1.条件与结论共6个：点A在抛物线上；点B在抛物线上；点D在抛物线准线上；A，O，D三点共线；A，F，B三点共线；直线BD∥x轴.它们之间有怎样的关系？通过变式探究，我们应该有所感悟！

2.这里只对变式2进行了拓展，显然其它变式同样可进行类似拓展.

3.各种变式中y2=4x易推广到y2=2px，让学生自己完成.

4.抛物线的焦点弦的性质非常多，让学生课后再去探究.

教学启示

1.正如美国著名数学教育家波利亚所说：“一个专心的认真备课的老师能够拿出一个有意义的但又不太复杂的题目，去帮助学生挖掘问题的各个方面，使得通过这道题，就像通过一道门户，把学生引入一个完整的理论领域”.[1]教师要研究教学，将课本上数学知识的学术形态转化为教育形态，让“冰冷的美丽”引起学生“火热的思考”.

2.纵观几十年的高考试题，信手可得到许多高考试题也来源于课本教材.教材中的例题习题具有典型性，示范性，同时也渗透着一些数学思想方法或提供某些结论.[2]因此，以本为本，重视对教材中的例题习题的深入探究，发现新的东西，是提高高考复习效率的最佳捷径.

[1]于世章.挖掘课本习题价值上好复习课[J].数学通报，2014(12)：36.

[2]刘飞.2014年高考数学安徽卷理科第16题的探究[J].中学数学教学，2014，(4)：43.