抽象函数与导数耦合
安徽省铜陵枞阳浮山中学 (246736)
刘东莲
抽象函数与导数耦合
安徽省铜陵枞阳浮山中学 (246736)
刘东莲
抽象函数与导数相耦合类问题,多是高考试题和高考模考试题的客观性试题的压轴题.多数学生一看到这类题,就有一种恐惧感.这里就2016年各地模考中,出现频率比较高的、比较典型的一些问题进行归纳分类解析,使读者读后对这类问题整体解答有一个比较清楚的了解和理解.
一、导数与代数式乘积类
这类问题解决起来,关键是根据多项式的不等式,解出变量的范围,从而知道对应导数值是大于零还是小于零,来判断出函数单调性的对应区间.
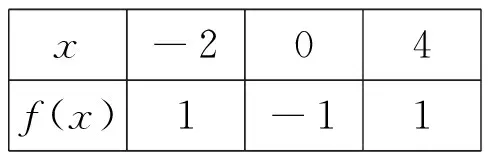
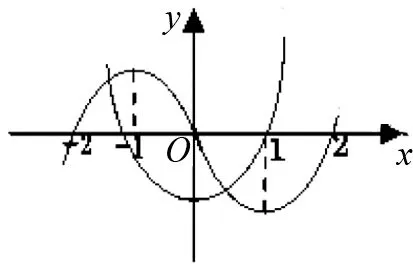
例1定义域为R的函数f(x) 对任意x∈R都有f(x)=f(4-x),且其导函数f′(x)满足(x-2)·f′(x)>0,则当2 A.f(2a) B.f(2) C.f(2) D.f(log2aa) 解析:因对任意x∈R都有f(x)=f(4-x),所以其函数图像的对称轴为x=2,且2a-2>2-log2a,又因(x-2) f′(x)>0,则当x>2时,f′(x)>0,即x>2时,f(x)为单调递增函数;当x<2时,f′(x)<0,即x<2时,f(x)为单调递减函数;又当2 图1 例2设f(x)是定义在R上的函数,其图像如图1所示,则不等式(x2-2x-3)f′(x)>0的解集为( ). A.(-∞,-2)∪(1,+ ∞) B.(- ∞,-2)∪(1,2) C.(-∞,-1)∪(-1,0)∪(2,+ ∞) D.(- ∞,-1)∪(-1,1)∪(3,+ ∞) 图2 解析:根据原函数的图像,所以可作出对应导函数的图像如图2.因(x2-2x-3)=(x-3)(x+1),又(x2-2x-3)f′(x)>0,所以当x∈(-∞,-1) ∪(3,+ ∞)时,(x2-2x-3)>0,同时f′(x)>0.当x∈(-1,1)时,(x2-2x-3)<0,同时f′(x)<0.故D正确. 解析:因f(x)=f(2-x),则f(x)的对称轴为x=1.又因x∈(-∞,1)时,(x-1)f′(x)<0.当x∈(-∞,1)时,f′(x)>0,即f(x)单调递增.则当x∈(1,+∞)时,f(x)单调递减.故知距离x=1越近,函数值越大.则b>a>c. 评注:这类问题的解首要是要注意到区间,导函数的符号,原函数的单调性,三者之间的有机结合和准确对应. (二)“配”成导函数的积,商关系 根据题给的条件,如何“配”成导函数的积和商关系,再根据导数的符号,来判断整体函数的单调性. 例5已知f(x)是定义在(1,+∞)上的连续可导函数,f′(x)为其导函数,e为自然对数的底数,若x>1有xxf′(x)>ef(x)成立,则当m>n>0时,有( ). A.mf(xn)>nf(xm) B.mf(xnm) C.mf(xn)=nf(xm) D.mf(xn)与nf(xm)的大小关系不确定. 解析:对式子xxf′(x)>ef(x)两边取对数得 解析:因f′(x)tanx+f(x)= 例7设函数f(x)是定义在(-∞,0)上的可导函数,其导数为f′(x),且有2f(x)+x f′(x)>x2,则不等式(x+2015)2f(x+2015)-4f(-2)<0的解集为( ). A.(-∞,-2015) B.(-2017,-2015) C.(- ∞,-2017) D.(-2015,-2013) 解析:因在(-∞,0)上,(x2f(x) ′=2xf(x)+x2f′(x)=x(2f(x)+xf′(x)).又因2f(x)+x f′(x)>x2,则(x2f(x)) ′=2xf(x)+x2f′(x)=x(2f(x)+xf′(x)) A.6 B.7 C.8 D.9 例9已知奇函数f(x)的导函数为f′(x),且x∈(0,+∞)时,x f′(x)-f(x)=x,若f(e)=e.则f(x)>0的解集为( ). A.(-1,0)∪(1,+∞) B.(- ∞,-1) ∪ (0,1) C.(-e,0) ∪(e,+∞) D.(-∞,-e)∪(0,e) 说明:本例不仅巧妙地应用“配”的功能,同时还用到不定积分,这些都需要解题者有较厚的功底. 例10函数f(x)在R上可导,且满足f(x)>-xf′(x),则关于x的不等式f(x-1)>(x+1)f(x2-1)的解集为( ). A.(-∞,1) B.(-1,1) C.(- ∞,0) D.(0,1) 评注:这类问题关键是一个字“配”,不是随便就能“配”的好和“配”的准.所以需要解题者对题意有深入地理解,其次运算基本功要十分过硬.否则就会出“河里挖藕,盲无目的”乱“配”. 用“eax”来进行“配”,是因为“eax”的导数有一定特殊性,这是这类问题解决起来的核心所在. 例11设函数f′(x)是f(x)(x∈R)的导函数,且f(0)=1,3f(x)=f′(x)-3,则4f(x)>f′(x)的解集为( ). 说明:本例,不仅巧妙地应用“e3x”来“配”的功能,同时还用到不定积分,这些都需要解题者要有较强基本功. 例13已知f(x)是定义在R上的可导函数,满足f(x)>f′(x),且y=f(x+1)为偶函数,f(2)=1,则f(x) 例14已知f(x)是定义在R上的可导函数,满足f(x)>f′(x)+1,f(0)=2016,则不等式e-xf(x)>e-x+2015(其中e是自然对数的底数)的解集为________. 解析:令g(x)=e-xf(x)-e-x,则g′(x)=e-x[f′(x)-f(x)+1]<0,则g(x)在R上单调递减.因g(0)=f(0)-1=2015,所以e-xf(x)>e-x+2015等价于g(x)>g(0),则x<0. 评注:这类问题关键是用 “eax”来“配”,至于其中参数“a”到底取什么值,这就要因题而定.不是随便就能“配”的好和“配”的准.所以需要解题者对题给的形式要分析和理解,其次运算基本功要十分过硬.否则就会出现“海中失控的小船,无任何目标”乱“配”. 这类题的设问主要与函数的奇偶性、周期性、单调区间、对称性等与导数相结合. 例16已知f(x)是定义在R上的函数,且满足f(-x)=f(x),f(x+2)=f(2-x),若曲线y=f(x)在x=-1处的切线方程为x-y+3=0,则该曲线在x=5处的切线方程为________. 解析:因f(x)满足f(-x)=f(x),f(x+2)=f(2-x),则f(x+4)=f(x),且图像关于y轴对称.又因曲线y=f(x)在x=-1处的切线方程为x-y+3=0,所以y=f(x)在x=1处的切线方程为x+y-3=0.则知y=f(x)在x=5处的切线方程为x+y-7=0. 例17已知f(x)是定义在(0,+ ∞)上的单调函数,且对任意的x∈(0,+ ∞),都有f(f(x)-log2x)=3.则方程f(x)-f′(x)=2的解所在的区间是( ). 图3 x-204f(x)1-11 以上就抽象函数与导数相耦合的题型的解题本质和方法进了分类解析,以便读者能从中领略到这类问题的常规做法,及其数学内涵.不足之处望多指教.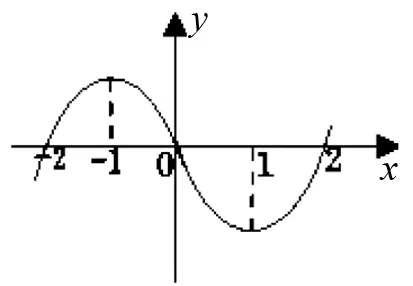
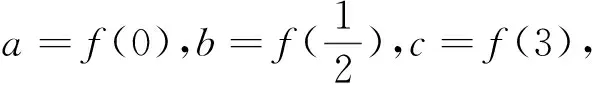
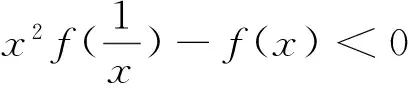
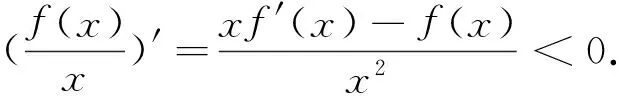
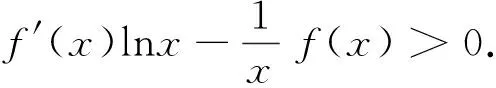
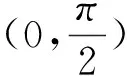
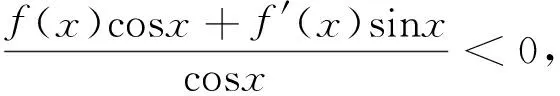
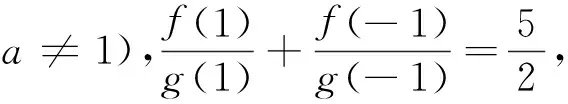
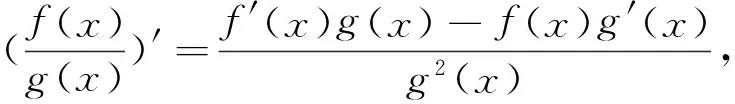
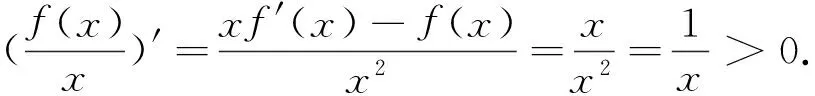
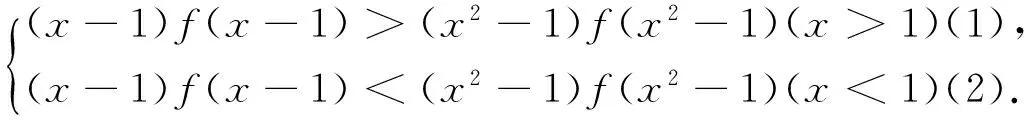
四、用 “eax”来“配”
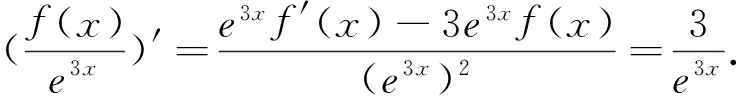

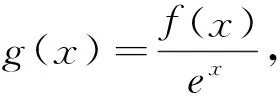
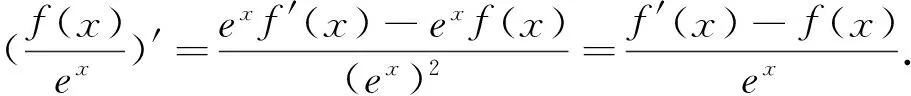
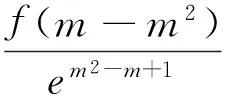
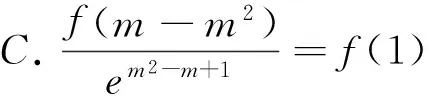
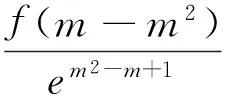
五、抽象函数的基础性质与导数