数学教学的理性、规范与举措

江苏苏州吴中区木渎实验中学 (215101)

周先荣

江苏省苏州市苏苑高级中学 (215000)

张国棣

数学教学的理性、规范与举措

江苏苏州吴中区木渎实验中学 (215101)

周先荣

江苏省苏州市苏苑高级中学 (215000)

张国棣

现代数学教师特别是年轻教师学历普遍较高，其中越来越多的教师不是师范科班出身.如何将专业知识形态转化为教育教学形态，形成有特色的个人核心专业素养，本文从理性、规范与举措几个方面来探讨，不妥之处，请斧正！

一、认识原理，生成理性思考

脚手架原理、思维迁移原理、最近发展区原理、原生态教学原理，这四个原理让我们更加理性的去认识教学，从宏观上指明了数学教学的行为走向.

1.脚手架原理

老师是学生学习过程中活动的脚手架.数学活动过程的基本特征是层次性，这种层次性通常表现为一系列的“台阶”，而台阶间的潜在距离往往左右学习的效率，距离远学生断了念头；距离近，吊不起胃口，教师必须运用“脚手架”原理给学生设置好“台阶”.这对老师要求很高，方法上具有高度的灵活性，思想上具有创新性，能够真正发展学生的内在品质：精神性、创造性、生成性、先进性、实用性、拓展性和时代性.

首先要调动学生的学习情感、激发学习兴趣.因为学习情感、学习兴趣的生成不是老师硬性规定的行为，而是一种非常自然的学习状态.然后，利用学生求新、好奇、渴望成功的心理特点和思考问题的方式，以及解决问题的行为习惯，创造出奇、合理科学的问题，激发学生智力与非智力因素出现最佳活跃状态，表现出勇于探索、大胆质疑的精神状态；观察敏锐、想象丰富、产生灵感的智力状态，形成学习的内在推动力.

2.思维迁移原理

发展学生的思维是数学教学的重要任务，而发展思维的重要方式又是思维迁移.人的大脑在思考问题时，会不断加入新的想法，将原先一些没有联系的事情整合成和谐的统一体.这种在一种情景下所学的内容，应用于另一种情景的现象，就是思维迁移.迁移过程包括两部分：①过去的学习经验对新学习的影响；②新学习内容在将来如何帮助学生.这一思维过程通常表现为：“行，是这样，那么然后呢？”.不言而喻的是，如果学生没有意识到现在学到的知识，在将来的情景中如何应用，他们就会对现在的学习给予很少的关注.

首先，要了解引发思维迁移的几种类型：正迁移和负迁移；课程发展引发的迁移；学习环境激发的迁移.其次，认识影响思维迁移的几个重要因素：知识和问题之间的相似性与关键属性以及关联性；学习情感与知识的掌握程度.最后，要把握如何在教学中更好地使用思维迁移：从过去到现在、从现在到未来的迁移；建立有效的联系通道；辨别关键属性，准确获得正迁移；情景模拟与搭桥等等.

90年代，美国心理学家Perkins和Salomon等学者研究认为：教师帮助学生从他们先前经验和其它新学习的内容之间找出联系，进行抽象概括从而激发思维迁移，这就是通常说的搭桥艺术.搭桥过程一般有三种方式：①要求学生找出解决问题的方法，讨论每种方法的优缺点；②采用类比的方法检查各个系统之间的相似点和不同点；③要求学生将现有问题应用于其他情景.搭起不同问题相互联系的通道，建立起思考问题的新模式，这对学生认识如何学习数学非常有帮助.

3.最近发展区原理

维果斯基的“最近发展区理论”，认为学生的发展有两种水平：一种是学生的现有水平，另一种是学生可能的发展水平，两者之间的差距就是最近发展区.教学应着眼于学生的最近发展区，为学生提供带有难度的内容，调动学生的积极性，发挥其潜能，并超越其最近发展区而达到更高的发展水平.把握“最近发展区”，让学生看到成功的希望，明确努力的目标，获得前进的动力，一步一步地发展自己，一点一滴地完善自己.

4.原生态教学原理

生物的生长和环境保护都要追求原生态.那么教育呢？什么是教育的“原生态”？它应遵循的规律是什么？作为教育工作者对这个问题思考过没有？思考过多少？教育的对象是学生、是人，所以，要谈教育的“原生态”，首先要确立以人为本的理念，以学生为本的思想，不能把学生仅仅看成教育的对象、认知的群体，更重要的是要把学生看成独立的生命主体.那么，教育就应该回归到本应属于生命主体的活动中去，回归到学生具体的年龄、成长阶段和时代背景中去施以自然有效的引导.无论是教育内容还是教育方式、方法都要少一点人为的雕琢，追求一种自然、和谐的原生态.

老师在原生态的教学环节下，当好脚手架，让学生的思维不断迁移，达到更高发展区，这样的教学理念不可或缺.

二、遵循原则，规范教学行为

核心素养原则、预设生成原则、难易转换原则、手段优化原则、因材施教原则，这五大原则能让我们更好的选择和优化教学行为，让我们的教学行为更加科学、合理.

1.核心素养原则

发展学生的核心素养，是数学教学的根本.教育部《关于全面深化课程改革落实立德树人根本任务的意见》指出：“核心素养是指学生在接受相应学段的教育过程中，逐渐形成的适应个人终生发展和社会发展需要的必备品格和关键能力.”重点指向：品格、毅力、自制力、好奇心、责任心、勇气、自信心等.数学核心素养的内涵比“思想方法”“能力”“技能”等更加广泛，它是知识、能力、态度和情感的融合，不仅包含学生的认知发展，又包括学生的非认知发展，主要体现在抽象、逻辑、建模、计算、直观、分析等六个方面.

不同学段对数学核心素养的理解也是不一样的.学生的数学核心素养总是在特定的情境和需要中反映出来的，其获得也是一个循序渐进、不断深化的过程，需要不同教育阶段的长期培养和教育的连续培养.在建立核心素养体系时，既要关注数学核心素养具备的普遍性，更要关注核心素养的个性化特征，如“个性修养、自主发展”等内容.如果忽视这些，只注重记忆概念、定理、结论，并通过大量的练习来强化应用，增加熟练程度，这最多只能是提高了学生的“技能”，是短视的功利的“分数”思想，是舍本逐末的教学行为.

2.预设生成原则

对课堂教学所作的预设和勾画只是一个蓝图，它应该是一个开放的系统而不是封闭的系统.无论课前作出多么周密的设计和预测，总还存在很多不可预知的因素，因此，这种预设决不是课堂教学中必须遵守的教条.教学中，要随时调整课前的预设，及时创造，即兴修改，创设出有利于学生进行有效学习的情景，这也是课堂教学的生成性.

科学家钱学森说过：“灵感，也就是人在科学或艺术创作中的高潮，突然出现的、转瞬即逝的短暂思维过程.”数学思维灵感的出现往往带有突然性，同时也可能转瞬即逝.这种机不可失的“妙微心会”，错过了就不会再来，往前走一步也许就能带来柳暗花明的新意境.教师要善于捕捉这样的瞬间，抓住机遇将“意外”变成“无法逾越的精彩”，“教学原本是即席创作.”

处理好教学方式预设性与生成性的关系是对把握课堂能力的考验.敏锐抓住瞬间生成的教学方式，保护和发展学生的探索激情，让学生的思维持续飞翔，使之既有“水的灵动”又有“山的沉稳”，进而“明明白白我的心”，这可能是我们所希望的课堂教学吧！

3.难易转换原则

大难至简，难的问题用简单的方法解决，从简单的问题发现深刻的道理.老师在构建问题时，要立足于学生实际，把握好难、易之间的潜在距离，让学生“跳起来摘桃子”.所以，难、易转换应具备以下几个特性：

(1)挑战性：能激发探究的欲望，促进学生积极参与，形成“不到长城非好汉”的学习韧性；

(2)体验性：能给学生提供深刻的体验，人人有所得，包括操作、探究的机会，让学生亲身感受、体验数学；

(3)可及性：问题要符合学生的一般认知规律、身心发展规律，包括学生的知识经验、能力水平、学习习惯、兴趣爱好、心理状况等；

(4)开放性：问题富有层次感，入手较易，开放性强，解决方案多，学生思维与创造的空间较大.低起点高要求，恰当把握问题的思维难度、思维跨度和思维梯度，才能使学生有不断探索的欲望，有利于学生思维的可持续发展.正如笛卡儿所说：“从最简单、最易懂的对象开始，依照先后次序，一步步达到更为复杂的对象”，这也是学生必须明白的学习之道.

4.教学手段优化原则

随着计算机技术的发展，新的教学手段不断出现，如网络、视频课件、微信、聊天室等,这也使现在的“翻转课堂”、“慕课”成为可能，并有受推崇之势.作为现代老师，掌握现代教学手段已经成为教师专业核心素养的一部分.然而，不论是教学工具和教学手段都要追求有效合理、自然，不能让ppt只是起到小黑板的作用，也不能为了追求“现代化”让课堂花哨而无用，关键是把握现代教育技术使用的“度”和效果.

5.新因材施教原则

我们的教学归根结底是以人的发展为本，涵盖生理、心理、品格、知识、素养等诸方面.二千多年来，教学很经典的“圣经”无疑就是“因材施教”.现代的因材施教，其中的“材”不应该是一个单一的、静止不变的概念，而是一个动态的、发展的概念.要用发展的眼光看待学生和教学，要以现在的教学为孩子将来的终身发展服务，它要求我们不仅要以学生的“实际发展水平”而教，而且要以学生的“潜在发展水平”而教.

三、引领探索，优化实施举措

数学教育教学，知识的传授、能力的提高是基本行为，核心素质的发展是重要行为，人的健康成长才是终极行为.老师要善于引领学生主动探索以下几个方面，这是学生健康成长所必备的基本数学学习行为.

1.引领探索生活中的数学

荷兰著名数学家和教育家费赖登塔尔(H.Freudenthal)认为：“数学来源于现实，且寓于现实中.”以这一思想为基础，要能够通过问题的构建和解决，浓缩升华为数学概念、运算法则、数学思想和数学理论，并在这种学习过程中掌握“数学化”的方法.同时，应当寻找数学知识在客观世界中的实际背景材料，把大量的数学好题置于学生所热爱的生活情境之中，让学生亲身体验数学的实际创造过程，从而提高学生从生活中发现数学的水平.这个过程，最重要的是能提炼数学思想方法，揭示数学本质.

学生作为认知主体感受到问题的存在，但问题的关键是什么？如何解决？用什么方式来解决？特别是问题背后蕴含着什么样的深刻道理？一般情况下，这些在学生的头脑中是一些模糊的印象.所以，问题的提出和解决，都要给学生提供自主想象问题、发现问题的空间，进而确定需要解决的实质性问题.正如爱恩斯坦所说：“提出一个问题比解决问题更重要，后者仅仅是方法和实验过程，而前者则要找到问题的关键和要害”.当然，这种“提出问题”是要拨开问题表面的浮云，重在数学自身的本质及价值的发现.

2.引领探索概念、定理的起源

数学概念、定理是组成数学知识的基本单元，是数学大厦的基石.学生对概念、定理的认知过程并不是简单的“死记硬背”，要探索如何由感性事例上升到对概念、定理的理性认识；探索概念、定理之间的相互联系与区别，克服思维定势的消极影响，发展学生思维的灵活性和发散性；探索概念、定理应用的多样性，找出对概念、定理理解上的缺陷并加以完善，克服“懂”而“不会用”的心理障碍等等.

另外，探究概念、定理发生、发展的历程，渗透数学史是数学教学的重要任务.当然，数学家们建立一个数学概念、定理往往需要经过漫长而曲折的过程，学生学习时不可能完全重复这一过程.这就要求教师精心选择典型事例，既不违背历史，又符合学生认知特点，引导学生对数学概念、定理的发展历程有一个正确的、深刻的、全面的认知.

3.引领探索公式变化、推广

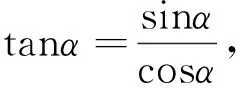
4.引领探索数学审美

一般认为，数学美分生活中的美和思维领域的美两个方面，包括数学的表现形式、应用形式、文化价值，以及思维领域的统一、和谐、简洁、奇异、逻辑、严谨等诸多方面.可以讲，数学美在形成人类的理性思维和促进个人智力发展的过程中发挥着独特的、别的学科不可代替的作用，这也正是数学的魅力所在.

新形势下，数学审美就是将数学美转变成为教育形态，是以培养学生发现数学美和欣赏数学美的能力，并利用数学美来陶冶情操、净化心灵，提高学习数学的兴趣和数学素养的教育行为.数学审美是蕴含在教学过程中，首先，让学生在数学学习的过程中潜移默化的感受到数学美，形成对数学“美”的赞叹，追求数学“完美”的渴望.然后，是以数学美“育人”.在使学生获得相应数学知识、数学能力的同时，更是培养学生美的情操.

目前，老师中对数学审美也有两种误解.其一，课堂教学首先考虑的是完成“应试”的教学任务，如果做不到这一点，宁可不要其他的不管是怎样美妙的旗号；其二，数学审美的研究还停留在相对肤浅的层次，有些还停留在“这些问题具有什么样的数学美”的层次.这使得数学审美有简单化之嫌，浮于表面虚张声势，好像只要把数学中的知识点和数学审美的概念挂上了钩，就是数学审美了.这些认识上的误区，也影响了实施数学审美的信念，要解决这些问题，关键是如何认识数学审美与数学教学的关系.

首先，数学审美是数学教育的重要组成部分，在掌握“知识和技能”中发现数学美，在感悟数学美的同时增加对数学的理性认识，可以讲，数学审美对数学教学有着“润物细无声”的作用.

其次，数学审美和数学本质水乳交融.任何问题，一旦逼近了事物的本质，符合了事物的规律，走进了真理的内核，她就必然是美的，正如海森堡所说：“美是真理的光辉”.同时，一旦感悟到了数学的美，自然就会进一步增加学生发现问题和解决问题的内动力，提高学习的兴趣和探索数学本质的欲望，这也正是李泽厚强调的“以美启真”.所以，数学审美和数学本质水乳交融.认识到这两点数学审美也就不会是“水中的月亮”.

5.引领探索数学史、数学文化

数学文化是以数学科学为核心，以数学的思想、精神、方法、技术、理论等所辐射的相关文化领域为有机组成部分的动态系统.莫里斯·克莱因在《西方文化中的数学》前言中指出:“在西方文明中，数学一直是一种主要的文化力量.”数学文化具有知识、理性、智力、美学价值，从数学知识的获取到数学方法的提炼，从数学思想的感悟到数学精神的弘扬，数学文化的这些价值将丰富数学教育的内涵，促进学生数学核心素养的形成.

数学史是数学文化的重要组成部分，如何研究数学史的教学价值，以下几方面不可忽视：

其一，数学史教学是数学精神的传承.我们对数学的认识经历了科学数学—思维数学—文化数学的过程，真正的数学史教学既是数学文化的传播，更是数学精神的传承.

其二，数学史教学是数学思维、理性的重要培育过程.数学史不是冰冷的文字、年代、事件，数学史也是火热的思考.数学的发展历程，每一个概念的建立，符号的发明，体系的完善，都是艰难的思考、淘汰、斗争过程.它不光淋漓尽致的展示了数学思维，更完美的展现了数学的理性.

其三，数学史对人的成长的影响.数学家不畏权贵的品格，刻苦钻研团结协作的精神，数学发展的曲折和血腥，数学甄没的遗憾，都是学生成长不可缺少的精神食粮.正如“新课程标准”指出的“寻找数学进步的历史轨迹，激发对于数学创新源动力的认识，接受优秀文化的熏陶，提高文化素养和创新意识.”

其四，教材上数学史料的星光闪烁.以江苏教育出版社《普通高中课程标准实验教科书(数学)》为例，数学史的呈现形式有边注、阅读材料、例题习题、探究案例几个方面，必修教材共5册一共有31处.分配如下：

类型阅读材料边注例题习题探究案例数量,占比17篇,54.8%7个,22.58%4道,12.9%3篇,9.7%

虽然星光闪烁，难明漫漫长夜.对数学史的渗透、体味可谓杯水车薪.这就需要我们通过更多的形式，补充适当的内容，让浩夜长明.

其五，中、西方数学史的比较研究.中国近百年是接受和学习西方数学，没能从精神、理性两方面来更深层的研究西方数学.西方数学具有明显的理性特点，古希腊奴隶主之间彼此平等，其社会底蕴是“证明”和说服.于是，“对顶角相等”虽然看起来十分显然，但仍然用“等量减等量，其差相等”的公理加以证明.中国古代有灿烂的数学成就，如《九章算术》，那是数学家向帝王提出如何“丈量田亩、征取税金、摊派徭役、计算土方”等实用数学问题的总结.在不对等的政治环境下，“对顶角相等”是不需要证明的，这也是我们过去没有建立完善的数学公理化体系的重要原因.可以说，古希腊和古代中国政治文化决定了两种数学文化的走向.

鉴于此，数学史数学文化的教学任务，主要是中、西数学史和数学文化价值观以及数学文化传统的介绍与比较.其中最重要的是让学生正确认识中国固有的数学文化传统，认识我们民族的数学文化传统技术和价值观是如何走向世界，并在接受西方数学的过程中发生改变，以及它在今后如何演变.只有在这些较为系统的数学史对比探索中，才能突出数学的理性精神，“以史为鉴”达到育人的目的.

6.引领探索实验操作

数学实验是计算机技术和数学软件引入教学后出现的必然结果.现在，初中有专门的数学实验教材，很多学校也都建立了数学实验室，目的是提高学生学习数学的积极性，提高学生对数学的应用意识，并培养学生用所学的数学知识和计算机技术去认识问题和解决实际问题的能力.通过学生的模拟观察、动手操作，对数之源、数之趣、数之美、数之用都有一个从感性到理性的升华.

[1]《普通高中数学课程标准(实验)》[M].

[2]普通高中课程标准实验教科书《数学》(必修)[M].江苏教育出版社.

[3][美]David A.Sousa(“认知神经科学与学习”国家重点实验室，脑与教育应用研究中心译).脑与学习[M].中国轻工业出版社.2005,2.

[4]李瑛华.学生主体参与数学课堂教学的基本策略、途径和方法[J].数学通报.2007,1.

[5]王晓军,张维忠.数学文化视角下课堂教学情境的创设[J].中学数学教学参考.2007,1-2.

[6]王宪昌.数学文化在数学教育中的地位[J].数学通报.2006.6.

[7]黄秦安.关于数学文化的若干重要相关研究领域——兼论如何进一步开展数学教育的文化研究[J].数学教育学报.2007,5.

[8]唐志华.数学史的教育价值及数学史志教育的策略[J].数学教育学报.2007,11.

[9]黄秦安.关于数学教育若干问题与现象的忧与思——兼论数学教育的学科建设[J].数学教育学报.2008,1.

[10]张国棣.谈中学数学的审美教育[J].数学通报.2010，12.

[11]张国棣.新课程教学应加强学生“探究”方向的指导[J].数学通报.2007，1.

[12]赵士元,张国棣.从中学的视觉看数学文化观念下的数学教学[J].数学通讯.2010,10.