数学教学要体现数学知识的意蕴
江苏省海州高级中学 (222023)
徐进勇
数学教学要体现数学知识的意蕴
江苏省海州高级中学 (222023)
徐进勇
知识的意蕴是指知识所蕴含的理性内涵,包括知识的价值、知识的精神、知识的情感等,它是知识的精义和主旨所在.[1]数学知识的意蕴是启动、维持与深化数学活动的引擎,是推动数学知识产生的内驱力.只有感知和领悟了数学知识的意蕴,才能理解数学的基本思想,才能领会数学思维的奥秘,才能把握数学的基本方法.所以,理解数学知识的意蕴是提升数学学科核心素养的前提.
一、数学知识的意蕴是在挖掘知识的过程中形成的
《普通高中数学课程标准》指出课堂教学应“努力揭示数学概念、结论发展过程,体会蕴涵在其中的数学方法,追寻数学发展的历史足迹,把数学的学术形态转化成学生易于接受的教育形态.”因此,体验、揭示知识发生、发展的过程,并进行合理有序的建构,是数学教学的核心任务.
在讲述三角函数概念时,笔者作了如下安排:
问题情境:水车的半径为r,若水车的中心正好处在水面上(如图1),水车在逆时针转动过程中,如何求水车上点P离水面的高度h?
问题1当转动角度α为锐角时,如何求点P离水面的高度?
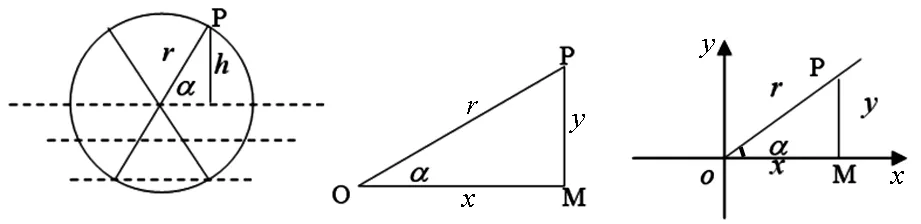
图1 图2 图3
问题2当水车转动角度α为钝角时,如何求P点离水面的高度?角度超过π?任意给定角度呢?
借助任意角的学习经验,现将图2三角形也放到坐标系中,如图3,你认为如何定义角α的正弦、余弦、正切?
学生主要有两种思考结果:
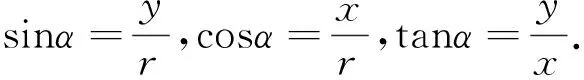
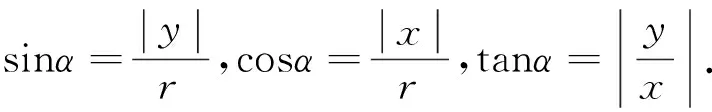
师:两种定义哪种更好?为什么?
生1:按结果1定义,和初中定义相同,但比值出现了负值.按结果2定义取绝对值,避免了负数的出现,但会出现终边不同时,比值会出现许多相等的情况,不容易分清楚.
师:比值出现负值时,点P在何处?
生2:负数的含义正好说明点P在水面的下方.
师生通过分析比较,统一认识,还是不取绝对值好,这样初中定义可以看成是现在坐标定义的特殊情况,而且也与要解决的问题相吻合.
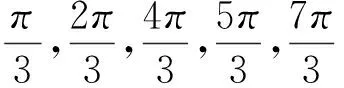
通过学生自主操作与小组交流,体会比值与点在终边的位置无关,与角终边存在一一对应关系,感受比值符号与终边所在象限的变化规律.
问题4情境中提出的问题如何解决?如果改为摩天轮,如何计算摩天轮上一点离地面的高度?(若摩天轮半径为10米,中心离地面的距离为11米)
通过以上4个问题,引导学生思考,在解决实际问题的过程中合理建构新概念,新概念的形成又为我们顺利解决问题提供理论依据.整个教学过程自然、自由、自主,体现数学源于生活并经理性分析与抽象升华形成严密逻辑体系的过程,让学生体会到数学的创新与应用价值,感受到自身的创造与潜能.
二、数学知识的意蕴是在构建知识的联系中形成的
科学知识是相通、相容、相生的,之间构成多种关联,形成共同的思想方法、情感态度与价值取向,可以为我们正确理解问题、解决问题提供多种转换角度与思路.教学中如能从问题的本质出发,多方联系,“引经据典”,一方面能触动学生的思维,打开学生的心智,促进学生理解,同时也能激发学生兴趣,增长见识,培养数学文化素养.
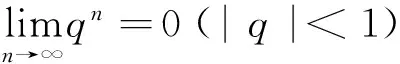
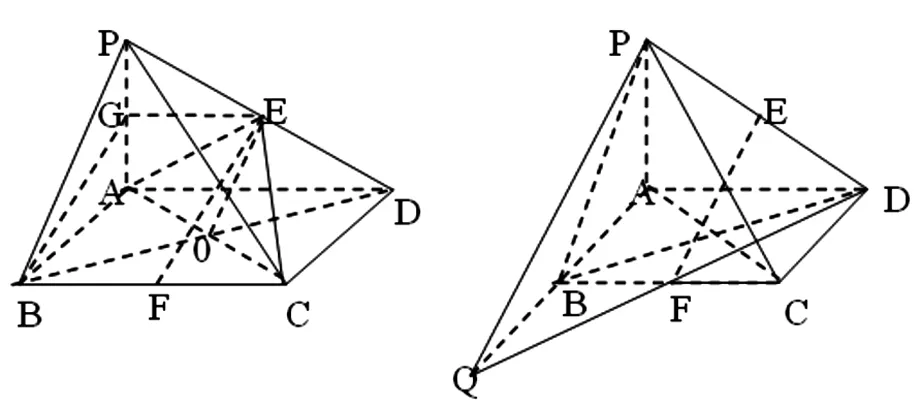
图4 图5
教师在讲授直线与平面平行时,为强化判定定理的应用(如果平面外的一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行),教学中可作如下安排:如图4,在四棱锥P-ABCD中,底面ABCD是平行四边形,E是PD的中点,(1)试证明PB∥平面EAC;(2)在边BC上是否存在一点F,使EF∥平面PAB?
教师在巡视过程中发现学生在证明第(2)问时大都采用将EF“平行投影”到面ABP上得直线BG,在此基础上教师利用第(1)问的证明方法启发学生用“中心投影”来证明,如图5得直线PQ.此时,教师通过插入多媒体展示“中心投影与平行投影在中西绘画中的应用”片段,如图6,让学生感受数学与艺术的完美结合,两者一个处于高度理性化的巅峰,另一个居于情感世界中;一个是自然科学的典范,另一个却是美学构筑的杰作.赞叹数学与艺术极其丰富的普遍意义.学生兴致高,理解透彻,印象深刻.不仅拓宽了学生思考问题的渠道,更是提高了学生理性思考这类问题的技能,为学生在平面内顺利找到这条直线提供抓手.
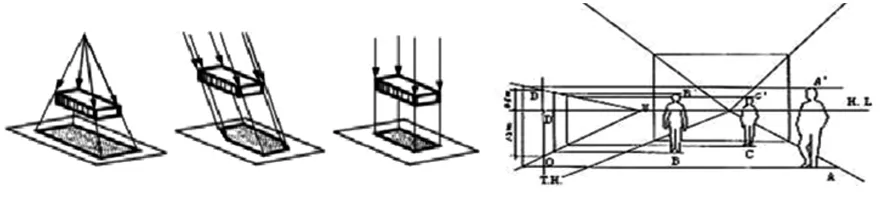
图6
人是感情的动物,人的思维状态与其情感有着密切的联系.用情感激活学生的学习心向,这是有意义学习的前提.在教学中只有注重情感教育,才能激发学生内在动力,才能使其乐学、好学、勤学,创造性地学.因此,数学教师要对数学知识理解得十分透彻,能抓住数学知识的本质,并不断挖掘数学与其它知识的联系,从感知到认知再到情感,达到“润物细无声”的教学效果.
三、数学知识的意蕴与数学的文化价值、美育价值有着天然联系
学科教育具有知识教育和文化教育两层含义:知识教育是基础,文化教育是知识教育基础上的文化升华.只停留在知识教育的基础上,不能从文化角度进行升华,则必然失去教育的深远意义.因此,必须从文化视角研究数学教学.数学文化是提高数学教育质量、进行教学改革的逻辑起点和突破口.
在讲数列概念时,课本“隆重”推出数列1,1,2,3,5,8,13,…,一方面反映该数列与现实生活相关联,如苏教版书中有插图显示树的枝杈数,同时也是下一步提出数列的递推公式概念的典例.教师可以安排《斐波那契数列与黄金分割》探究性课题,以增强学生学习数列的兴趣,提高学生认识世界、探索自然的积极性,体现学习数列的价值与意义.课题内容可作如下安排:意大利数学家斐波那契(1170-1250)1202年在《算盘书》中从兔子问题得到斐波那契数列1,1,2,3,5,8,13,…,并没有进一步探讨此数列,且在19世纪初以前,也没有人认真研究过它.几百年后,19世纪未和20世纪,这一问题派生出广泛的应用,从而活跃起来,成为热门的研究课题.斐波那契数列定义:若一个数列,前两项都等于1,从第三项起,每一项是其前两项之和,则称该数列为斐波那契数列,其递推公式是
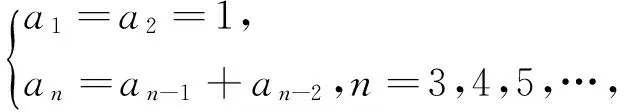
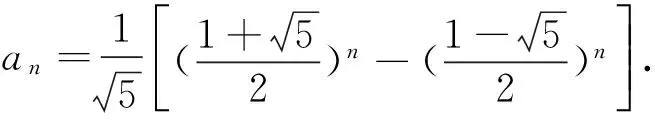
新课程标准非常注重知识的运用与文化的渗透,明确给定了数学建模与数学文化的教学建议与教学要求,提出了要开展研究性课题的探索.以数学发展中蕴含的思想方法为纽带串联知识应用的教学,为知识应用教学设计增添了新的视角,使得课时教学呈现形散而神不散的特点,教学的知识性、技能性、思想性都有所增强,对学生素养的培养更为全面.
四、数学知识的意蕴只有在领悟知识的本质、解决数学问题中得到理解
数学源于生活,又高于生活服务生活.学习数学的意义不仅在于知识本身和它的内涵,更由于它广泛的应用价值.结合近年来国家对食品、礼品的包装提出“摒弃奢华包装,力求朴素节俭”,笔者以此为背景,在导数的应用中安排了一节数学应用课.
例1如图7,有一个各条棱长均为a的正四棱锥,现用一张正方形包装纸将其完全包住,不能剪裁,但可以折叠,则包装纸的最小边长是多少.

图7
例2某商场为促销要准备一些正三棱锥形状的装饰品,用半径为10cm的圆形包装纸包装.要求如下:正三棱锥的底面中心与包装纸的圆心重合,包装纸不能裁剪,沿底边向上翻折,其边缘恰好达到三棱锥的顶点,如图8所示.设正三棱锥的底面边长为xcm,体积为Vcm3.在所有能用这种包装纸包装的正三棱锥装饰品中,V的最大值是多少?并求此时x的值.
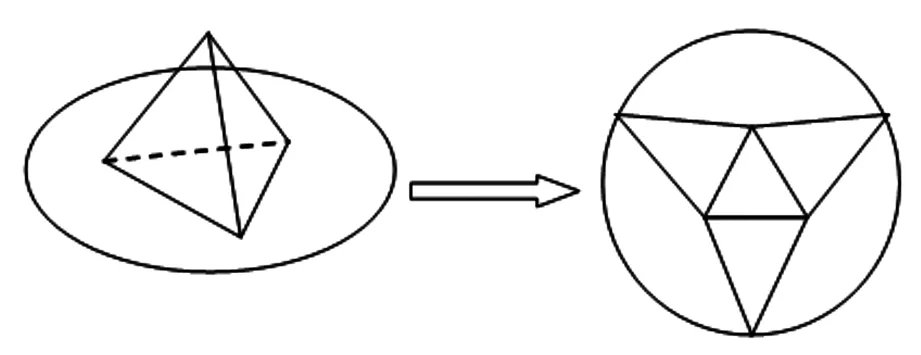
图8
例3(2011年江苏数学卷第17题)请你设计一个包装盒,如图9所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm.
(1)若广告商要求包装盒侧面积S(cm2)最大,试问x应取何值?
(2)若广告商要求包装盒容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.
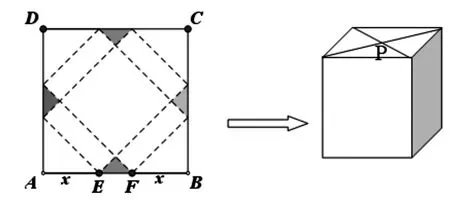
图9
解决上述包装问题的关键是把立体图形展开为平面图形,通过两种图形的联系建立目标函数,结合函数式特点求最值,过程中学生学会解决一类问题的方法和处理最值问题的一种手段.我们常见的市场销售问题、节约用水用电问题、运输问题、税收问题、医疗费用问题、银行储蓄问题等,都是以生活实际为背景,这些教学的具体素材,可以使学生进一步了解数学科学与人类社会发展之间的相互关系,学生运用所学的知识和方法解决了这些问题,获得了成功的享受,并能更好地理解数学知识与数学方法.
教学中突出知识的意蕴,就是在知识教育基础上,上升到心灵与智慧的培养、价值观念的形成和精神陶冶上,充分利用数学知识和相应的其它一切可以利用的文化资源,进行文化积累和文化升华,以实现审美、陶冶、文化遗传的教育功能,从而为认识自然和社会,适应生存环境,并能够创造出新的人类文明作出应有的贡献.教学中突出知识的意蕴,正是使得“教育是知识获得过程”向“教育是文化过程”转变的最有力的手段和契机,从而能够真正实现教育是“通过摄取吸收文化价值,体验陶冶多维的人,促进生命个体总体生成”的文化过程[2].
[1]章建跃.数学知识的意蕴与数学素养的提升[J].中小学数学,2015(6):封四.
[2]赵祥麟.外国教育家评传-斯普朗格[M].上海:上海教育出版社,2009.
* 本文为江苏省教育科学规划2015年度研究课题(D/2015/02/095)《现代数学教育观下高中数学文化课堂的实践研究》阶段成果.

