波利亚解题表助力学生解题能力提升

江苏省海门中学 (226100)

陶炳宏

波利亚解题表助力学生解题能力提升

江苏省海门中学 (226100)

陶炳宏

调查发现，学生在数学解题中存在的问题一般有如下几个方面：1.基础知识的理解、基本问题基本方法的掌握不够扎实；2.没有良好的数学解题习惯，如审题不够仔细、计算失误、解题过程缺乏条理性、步骤之间的逻辑链条不严谨、没有检验环节等；3.习惯于模仿的方式解题，不善于进行方法迁移、问题转化，碰到陌生一点的问题往往思路打不开，缺乏主动思考探究的习惯.经过高三一轮复习以后，对于上述问题1学生基本都能克服，但由于问题2、3难以短时间内克服，导致学习成绩难以从良好向优秀跃升，也很难获得数学解题成功带来的兴趣提升.笔者在教学实践中考虑在解决第1方面问题的基础上，如何解决第2、3方面的问题，真正培养学生分析问题解决问题的能力，培养学生缜密的数学思维能力和良好解题习惯.著名的数学教育家G·波利亚在其经典著作《怎样解题》一书中给出了“怎样解题”的解题表，被各国数学界奉为数学解题宝典，如果在教学实践中注意引导学生按照“表”中的问题和建议思考，探索解题途径，进而逐步掌握解题过程的一般活动规律，把解题表的掌握与自觉运用作为数学教学的重要目标之一，让学生逐步形成良好的解题习惯，解题能力得到明显的提高.

1.波利亚解题表引导数学思维有序前行

一般情况下，学生面对一道稍具挑战性的问题，首先想到这个题目老师讲过没有?如果老师没讲过，或讲过但已经没有印像时，就处于思维封闭状态.如果有老师在边上，关键时刻能提示一下，就可能一步步接近成功.现实是老师不可能一直跟在身边，但如果有一张表，表上为一系列的提示性问题串，根据问题的提示一步步思考，那是一个很不错情况，波利亚解题表恰好就是这样的一个表，表中第一个提示性问题是：题目告诉我几个什么条件，分别是什么？题目到底是求什么？第二个问题是：由每个条件想到了什么？条件与条件相结合想到了什么？第三个问题是：由所求问题想到了什么？有没有做过类似的问题(第二、第三问笔者结合自己理解和教学实践的表述)然后把第二、三问题的所想所得的发现记录下来，再以记录所得的发现重复第二、三问，这样层层递进，思维就会被逐渐激活，同时条件与结论之间迷雾就会被逐渐驱散，直至两者之间实现完全对接,找到思路.

例1(15年全国高考新课标2卷)设函数f′(x)是奇函数f(x)(x∈R)的导函数，f(-1)=0，当x>0时，xf′(x)-f(x)<0，则使得f(x)>0成立的x的取值范围是________.

首先，这是一个填空题：题目告诉我几个什么条件，分别是什么？题目到底是求什么？，弄清题目条件有3个要点，分别是：①奇函数；②f(-1)=0③当x>0时，xf′(x)-f(x)<0；问题是：求解f(x)>0(Q)

再根据第二个问题:由已知条件想到了什么？条件与条件结合又能得到什么？

由①想到图像关于原点对称，f(0)=0④

由①②结合得f(1)=0⑤

得到新结论⑤后重复第二个提示性问题

③是条件中比较关键的，由③想到了什么？如果想不到怎么办？那就考虑可以和谁结合起来.③⑤结合得到f′(1)-f(1)<0，即f′(1)<0⑥;

⑤⑥结合得到x在1左侧f(x)>0；1右侧f(x)<0⑦；

图1

由⑦思考在(0,1)上是否存在下穿x轴或与x轴相切的可能呢？假设存在点C(xc，0)与③结合，xCf′(xC)<0，即f′(xC)<0，由图1可以看出f′(xC)≥0，所以这样的C点不存在，(0,1)上f(x)>0⑩.

⑨⑩与①结合得到f(x)>0的解(-∞,-1)∪(0,1).

思维链条图：

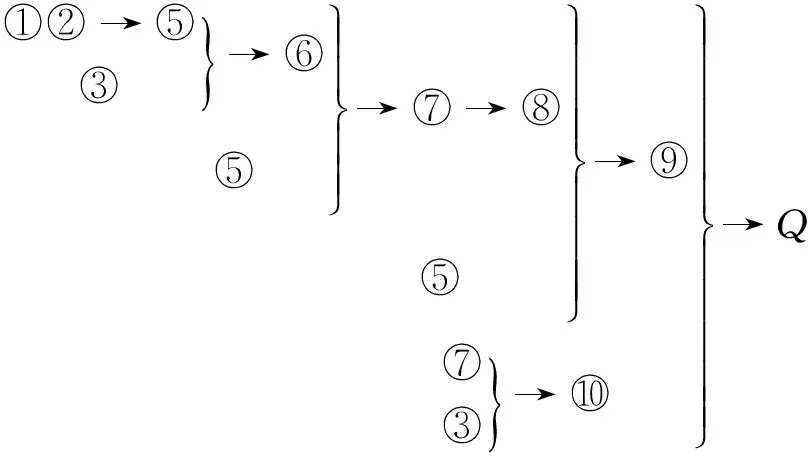
对于思维的拓展，波利亚解题表从不同角度给出了对多数数学问题具有引导价值的普适性提示问题.从问题出发有“如果不能解眼前的题目，能否找到一道与之有关的问题？一道更为普遍化的问题？一道更为特殊化的问题？一道类似的问题？能否利用联想到的问题的结论呢？能否利用联想到的问题的方法呢？”从条件出发，可以有“我能解出这道题的一部分吗？只保留条件的一部分，结论又该如何变化？回到条件中所涉及的概念定义中去，又有何发现？还有什么条件没用到？能不能按题目所给条件画个图？……”所有这些提示，对于活跃思维，乃至成功解题都有很大帮助，当学生对于表中的提示从开始有意识的应用到无意识应用时，便达到了令狐冲独孤九剑中无招胜有招，真正掌握了数学思维方法.

2.波利亚解题表引导良好解题习惯的形成

波利亚的解题表将解题过程中分为四个环节：理解题目、拟定方案、执行方案、回顾.四个环节中最为核心的当然是第二个环节拟定方案，其实质是寻找解题思路的过程，但正是因为学生太重视这个环节而忽视其它环节，往往形成了不好的解题习惯，导致会而不对、思考不够细致深入等毛病.如果引导学生养成按波利亚解题表进行解题作业，并最终养成习惯，对学生的数学学习必然存在极大的帮助.第一个环节理解题目中，本质是审题：未知量是什么？已知数据是什么？条件是什么？再深入一点，条件是否足以确定未知量？或者不够充分？或者多余？或者矛盾？第三个环节执行方案，这个环节实质是找到解题思路后的解题实施，有的学生好不容易找到解题方法，但胜利冲昏头脑，解题时不够沉着导致失误.这时应该问问自己，“我检查每一个步骤，能否看出这个步骤是正确的吗？”

第四个环节回顾，一道题目做完就扔是大部分学生的习惯，实质上对于一道好题解完之后的回顾往往包含着更大的收获.回顾1.“你能检验这个结果吗？”可以达到从不同的角度审视这个问题的结论，如此一方面可以确认这个题是否做对，同时又能从不同的角度加深对问题的理解.回顾2.我能用不同的方式推导这个结果吗？能推广这个结论吗？扩散思维，力争一题多解，把问题想深想透.回顾3.我能在别的什么问题中利用这个结果或这种方法吗？把这个问题的价值最大化的发挥出来.接例1

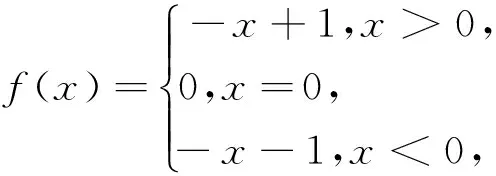
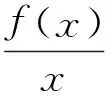
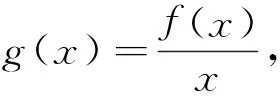
从上述过程可以看出，回顾就是对解题过程的准确性加上了一份保证，同时也是一个通过解一道题尽可能获取更多效益的过程.

一个数学优秀的学生往往由于无意识中养成了良好的思维习惯，进而在一次次的攻克难题的过程中培养起了面对难题的不轻言放弃的品质和积极的心态.教师通过理解解题表、应用解题表思考问题继而在教学过程中可以尝试利用解题表对学生思维有意识的引导，规范学生解题习惯，可以实现学生解题能力质的飞跃.