《数理逻辑和集合论》讲课用例的设计和构造

王拥军， 杨义川， 宁云转

(北京航空航天大学数学与系统科学学院，北京100191)



《数理逻辑和集合论》讲课用例的设计和构造

王拥军， 杨义川， 宁云转

(北京航空航天大学数学与系统科学学院，北京100191)

《数理逻辑与集合论》是数学、信息、哲学和计算机科学等专业的重要基础，但其高度的抽象性特点往往使得学生望而生畏.课程教学中不能只强调抽象的、难以理解的符号系统，而必须立足于使学生拥有很好的直觉认识能力.在教学过程中有意识地选择数学和信息科学中学生们熟悉的典型实例，精心设计和构造以帮助学生理解相应的抽象概念，在温故知新的基础上，大大拓展了学生视野，对理解抽象概念起到事半功倍的成效.

数理逻辑； 集合论； 抽象； 讲课用例

1 引 言

在《数理逻辑与集合论》课程的教学实践中[1,2]，切实感觉到讲授概念时，恰当实例的缺乏已经严重影响学生的学习兴趣、理解深度和学习效果.因此，我们多年来的教学研究与实践工作之一，主要集中于构造和设计合适的课程用例.即从学生熟悉的数学学科和感兴趣的信息学科[3]中选取相应实例，精心设计和构造以帮助理解相应的抽象概念[4]，达到让学生喜欢并主动参与的目的，进而引导他们想象“抽象”，最终理解“抽象”.

1.1 课程的高度抽象性特点

逻辑是确定思维有效性的形式规则系统，用数学的方法研究关于推理、证明等问题的学科叫做数理逻辑，它的研究对象就是符号形式语言和各种形式系统.而Cantor集合论作为数学大厦的基础，存在着不可回避的逻辑悖论.目前解决这一问题的基本思想是集合论的公理化，所以数学的基础又被归结为公理集合论.本课程的两部分内容涉及的概念均表现出高度抽象的特点，很难简单借助对以往知识的感知来把握.诸如：由公理给出的形式群理论不能完全等同于抽象代数课程中的群理论，承认无限公理之后的各种无穷集合很多性质不同于学生熟知的有限集合，等等.

让学生们能想象、理解这些重要而基本的概念和原理，使学生们认识到这些问题和生活实践、学科背景密切相关，由对本课程产生兴趣进而提高对整个学科的理解，应当是教学任务中的重点和难点.

1.2 课程建设中的问题分析

(i) 教学实效性有待于进一步提高.经常是教师很辛苦地证出一个结果之后，学生虽然在理论上同意你的每一步推导，但心中不太认可这个仅由变形法则保证的结论.这往往使得课下巩固很难，碰到习题无从下手，久而久之，开始的热情大打折扣，变得敬而远之了；

(ii) 对实现教学目标的途径、形式的研究有待于加强.学生们喜欢鲜活、生动的形式，喜欢在创造中体会学习的快乐；

(iii) 对本课程教学规律和学生的认知规律研究有待于深入.以公理化方法引入概念，讲解高度抽象的形式系统，极易使得课程内容变成脱离实际的符号游戏，很难和学生们的直觉挂钩，这个看起来“高深且没什么用”的课程就会被束之高阁.

1.3 为何选择以设计课程用例作为突破口

针对上述问题，我们认为提高兴趣、突出直觉有利于帮助理解抽象概念，是解决问题的一个很好的突破口.

大家都知道，尽管用“1头牛加上2头牛，数一数是3头”来解释“1+2=3”是远远不够的，也是非理性的，但对于我们初始理解这样一类抽象式还是有所帮助的，这里对牛的直觉就是“抽象概念具体化”.必须再次和反复指出的是，抽象一旦具体，就不再是一样的含义了，就像2头牛、2只香蕉…，永远不是2的真实意思一样.但具体化可以使学生获得思考的养料，借用他们熟悉的角度理解和印证抽象的问题，逐步接近和把握概念的本质[5].

数理逻辑和集合论是数学大厦的重要基础.针对其自身特点和整个课程体系的限制要求，教学点应当围绕数学形式系统展开.数学形式系统是抽象的，理解有时是相当困难的.这表现在解释形式系统的模型有时也是相当抽象的，比如形式群公理系统的一个标准解释是《抽象代数》课程中的群，此外还存在不是群的其他解释.如何给学生以恰当的直觉，不是一件容易的事情.

《数理逻辑和集合论》课程用例的设计与构造就可以这样入手，比如利用《抽象代数》课程中的群理论，感知数学系统和逻辑系统的联系，理解数学研究过程的解释和模型.因此，针对不同抽象问题点，在学生熟悉的数学课程或感兴趣的信息课程[6]中寻找具体模型，设计构造讲课用例，是一项有现实意义且颇具挑战的工作.

2 设计构造的讲课用例

以下几个从不同课程中提炼、构造的设计用例，更多地从学生们熟悉的数学领域觅得.它们的简单和清晰有助于理解复杂和抽象的概念.

2.1 利用代数实例理解逻辑系统

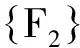
证令映射f∶{T,F}→F2如下：F对应0, T对应1；

f(a⊕b)=f(a)+f(b), f(a∧b)=f(a)·f(b)，

则易证真值集{0,1}在⊕和∧运算下与F2同构.

注 本例很简单，作用却不小.除了向学生指出逻辑真值集上的逻辑连接词“并不奇怪”，而是“似曾相识”外，还帮助同学们通过抽象代数里的最简单有限域概念与逻辑学间的直接联系，做到温故而知新.

2.2 对选择公理的理解

选择公理对任意集簇C，存在以C为定义域的选择函数g，使得对C的每个非空元素x，总有g(x)∈x.

选择公理的解释就是能够为任意集簇选择出一个集合，使得这个集合与集簇的每个非空元素相交不为空.学生们对于这个公理往往觉得很奇怪，因为以有限集簇为例这个定理显得很平凡，而思考无限集簇又会觉得很难把握，所以学习后往往陷入“知道又不真理解”的境况.

利用《拓扑学》、《数学分析》课程中大家熟悉的闭点、函数连续性构造设计讲课用例.使得学生在学习此两例的过程中，理解这个有些“莫名奇妙”公理的作用.其中收敛序列存在性的问题，正好说明选择公理在现代数学中的基础地位.

设计用例2闭点的定义 对于任一正实数ε，存在nε∈，使得对所有n≥nε都有成立，称实数序列xn|n∈收敛于a∈，这里表示自然数集合.

设A是一实数子集合，A的闭点通常有如下两种定义

以上二者等价的证明如下

(i)→(ii) 任给ε>0,存在nε∈,使得对所有n>nε都有成立.即有xnε∈A且ε.

关键问题在于(ii)→(i)时，xn|n∈序列果真存在吗?

当选择公理不成立时，我们没有把握能从非空集簇{Xn≠φ|n∈}选出xn∈Xn|n∈序列.因此，这两个闭点定义的等价实际上是依赖于选择公理的.

设计用例3函数的连续性

实值函数的连续性定义一般有如下两种

(i)f∶→在a∈处是连续的.如果对任意ε>0，存在一个δ>0使得对于所有满足的x，都有成立.

(ii)f∶→在a∈处是连续的.如果对任意收敛于a∈的序列xn∈|n∈，有序列f(xn)∈|n∈收敛于f(a).

以上二者等价的证明如下

(i)→(ii) 如果xn|n∈收敛于a且给出ε>0，首先可以找到满足(i)要求的δ>0，使得对于所有满足的x，都有成立.由于xn|n∈收敛，则由序列收敛定义知道存在nδ∈，使得当n≥nδ时有成立.当然，对于所有这样的n有成立.

问题在于(ii)→(i)时，xk|k∈序列果真存在吗？

这个证明过程中，δ分别取{1/k|k=1,2,3,…}时获得的序列xk∈|k∈隐含使用了选择公理.因为对每个1/k，并不是只有唯一的xk满足但ε.事实上有无限多的xk满足这一点，而这些xk中也未必有最大的或者最小的，所以(ii)→(i)证明过程中隐含使用了从这些无限多的xk中选择一个，继而组成序列xk|k∈的手段，这就是使用了选择公理.

关于选择公理的设计用例，还有相关《泛函分析》、《线性代数》等几门课程的，限于篇幅，这里不再一一给出.

2.3 关于计算机科学逻辑基础的理解

数论、代数和拓扑学深深得益于《数理逻辑与集合论》的丰硕成果，特别是计算机科学，几乎就是数理逻辑研究发展的里程碑.

设计用例4从介值定理体会计算机科学的构造主义本质,进而理解逻辑主义和构造主义的不同(优劣).

介值定理对于一个闭区间上的连续函数,若区间两端的函数值异号,则至少存在一个零点.

我们知道,构造主义只认可那些有限步可以构造生成的数学对象,这样从自然数开始不能得到无理数.因此，定理就只能在有理数意义下使用，很明显，这种情况下零点未必存在.

这里有两个启示:一是在计算机(没有无理数)中介值定理并不严格成立，只能近似获得零点；二是若承认构造主义，便会抛弃很多数学分析中的现有成果.

通过这个实例的讲解，难以理解的计算机科学的逻辑基础为学生直观接受，并能猜想、展望未来计算机需要的数学基础.

2.4 对无限和有限的认识

无限概念是现代数学不能回避的，种种矛盾和对立的观点都是由于不能准确把握它而引起的.如何看待“无限”是不同逻辑学派一个重要的分歧点.我们熟悉的《数学分析》使用潜无限概念(极限定义),公理集合论是认可实无限存在的(归纳集合存在公理)，集合论的主要工作是面对“无限”这个抽象概念，学生必须学会新环境中的思考方式和方法.

设计用例5定义：良基集合是指其任一子集合,都有极小元.

问:满足字典序的集合是良基的吗？

这个问题的解答很容易受直观的影响,因为大家所用的字典的任意子部分按照字典序总是有首单词的,所以答案往往是肯定的.这就是典型的以有限环境下的经验指导无限环境的实例.我们知道，所谓单词就是字母的有限可重复序列，但这样的单词有无限多个.如果按字典序一一排列，甚至永远排不到B打头的单词，因此，很容易构造一个子集合，这个集合没有极小元.如

{…,AAB,AB,B,BA,BAA,…}.

体会：(i) 有限和无限有本质的区别；(ii) 以有限枚举的方式不可跨越无限.

值得指出的是：这个实例由学生提出，源自于程序设计语言理论.学生们能不拘于传统词典的有限性实质，依照课程教学给出的形式概念正确思考本质无限的问题.这真的使我们坚信，设计和构造讲课用例是一个教学相长的过程，能充分激发学生学习兴趣，把他们吸拢来主动思考，也算是课堂教学的新境界了.

2.5 形式系统与模型的关系

关于形式系统和模型的联系，是通过一个映射实现的.本来它们之间是抽象与具体的关系，可是当模型本身也很抽象的时候，学生们很难区分形式符号系统和解释模型.这里的课程用例就是来源于学生们的一个问题：“数理逻辑中的形式系统和抽象代数里的理论哪一个更抽象？”

我们知道，任何数学形式系统都是谓词演算的一致扩充(不同的数学形式系统只是增加以不同的数学公理而已)，这些个数学形式系统之间除了共同的逻辑公理之外，还有三条共同的关于等词的数学公理.也就是说，所用的数学形式系统中都有等词.注意，这里的等词是个特殊的二元谓词符号，其性质仅由三条等词公理保证.等词不能简单地理解成以往的“等号”.

(E1) (x1=x1).

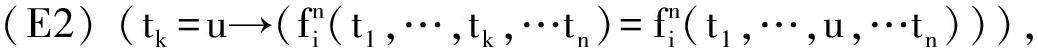
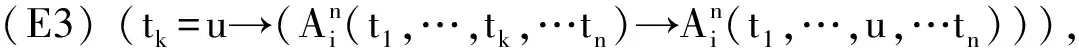
可以证明(因为和目的无关，所以不给出过程)，这三条等词公理仅能保证等词“=”具有自反性、对称性和传递性.所以，这其实只是一个等价关系，并不是数学中一般使用的等号含义.

设计用例6为了回答学生们的“孰更抽象？”的问题，下面给出一个特殊的数学形式系统—形式群理论.

当然，形式群理论除了包含谓词演算的六条逻辑公理模式、三条等词公理之外，还有如下三条群公理

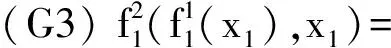
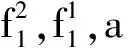
形式系统是符号的世界，通过一个映射就可以将符号对应到一个具体讨论的领域(模型)，使之拥有公理约束的具体行为.映射不同，具体模型就不一样.

更能说明问题的是个反例，那就是存在映射使得满足形式群公理约束的模型不是《抽象代数》课程意义下的群，具体如下：

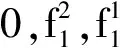
此例在教学实践中很好地帮助学生们理解了形式系统与其模型的关系，使得学生体会到抽象与具体的相对性.更重要的是，他们初步感知到数学大厦下隐藏的、更一般的数理逻辑基础.

3 讨论和思考

课程教学不能只强调抽象的、难以理解的符号系统，而必须立足于使学生拥有很好的直觉认识能力.

可以说，构造实例在教学实践中达到了设计效果.不仅提高了学生们理解抽象概念的能力，解决了“这些概念有什么用的问题？”，还加深了大家对实例来源课程的再认识.学习《数理逻辑和集合论》课程的目的应该是将抽象的理论再应用于实践.因此，实例的另一功效在于引导学生重新认识已学课程中的一些内容，比如分析中的无穷小量、证明中的数学归纳法等等.

本课程的教学研究和实践告诉我们：面对抽象概念，应当尽可能对具体内容加以更多的关注，使得学生容易跨过最初的认知门槛，养成抽象思维的良好习惯，帮助学生及时找到认知基础和知识生长点.例如在集合论中，数学家关心的是抽象的、普适的理论问题—公理系统的各种性质.而学生们往往首先关注的是一些具体集合的性质，如各种常见集合、关系、映射是什么样的；再如，从信息和计算角度来看，需要让学生知道计算机科学中的数理逻辑.这些都要求学生要建立判断的“直觉”基础，不能只是“漂亮”的抽象楼阁；另外，本课程教学还应当关注数理逻辑相关学科的发展史，例如非欧几何、非经典逻辑、量子力学、泛函分析等，都与数理逻辑相互影响，互相推动.关于这一点，将在其他文章中阐述.

设计和构造讲课用例，实际上是和学生一起于熟悉的领域温故，继而激发他们对本课程新概念的兴趣，借助这种直觉进入“抽象”领域，达到知新的教学效果.因为这种“抽象”是和某个“具体”相联系的，所以能起到容易接受并逐渐理解的目的.

总之，教学功夫在课外，想办法吸引学生主动参与教学过程才是重中之重.

[1] Hamilton A G.Logic for Mathematicians[M].北京：清华大学出版社(影印版)，2002.

[2] Karel Hrbacek, Thomas Jech.Introduction to Set theory [M].3rd ed.New York: Marcel Dekker, 1999.

[3] Bruno Marchal.Theoretical computer science and the natural sciences[J].Physics of life reviews, 2005, 2: 251-289.

[4] 张玲玲,黄建华,黄立宏.研究生数学公共课程中教学案例创新与建设的思考[J].大学数学,2015,31(3): 117-121.

[5] 李雨生,郭镜明.引导学生从掌握本质中提高学习兴趣[J].大学数学,2014,30(6): 120-122.

[6] 陈意云，张昱.程序设计语言理论[M].北京：高等教育出版社，2010.

The Design and Construction of Lecture Instances for Mathematical Logic and Set Theory

WANGYong-jun,YANGYi-chuan,NINGYun-zhuan

(School of Mathematics and System Sciences, Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

The course “Mathematical logic and set theory” is an important foundation of Mathematics, Information science, Philosophy, and Computer science, etc.But its high abstractness is main obstacle to learn this course for students.Teaching method should be based on training students′ keen intuition ability rather than only focuses on abstract and incomprehensible symbol systems.In the teaching practice, we consciously choose some classical instances for students from Mathematics and Information science which are familiar to them, then carefully design and construct lecture instances to help students understand relevant concepts.The practice shows that our instances can largely broaden students’ horizon and are very helpful for them to understand the abstract concepts based upon the famous Chinese education idea of “reviewing makes learning new”.

mathematical logic； set theory； abstractness； lecture instances

2016-05-18 ； [修改日期] 2016-07-15

国家自然科学基金(11271040)；基础科研基金(YWF-14-SXXY-015)；凡舟教学团队建设，北航重大教改项目

王拥军(1970-)，男，博士，讲师，从事软计算，数据挖掘研究.Email:wangyj@buaa.edu.cn

G640

C

1672-1454(2016)06-0117-06