高师院校数学专业三基课程关联性教学的研究与探讨
盛兴平, 唐 剑, 辛大伟, 徐传友
(阜阳师范学院数学与统计学院 ,安徽阜阳236037)
高师院校数学专业三基课程关联性教学的研究与探讨
盛兴平, 唐 剑, 辛大伟, 徐传友
(阜阳师范学院数学与统计学院 ,安徽阜阳236037)
高师数学专业的学生,首先面对的就是“三基”课程——《数学分析》、《高等代数》、《空间解析几何》的学习.本文主要从三基课程在内容上的联系、在教学上的关系、在解题技巧上等多方面研究了三基课程的内在关系,从而进一步促进三基课程的教学改革.
“三基”课程; 关联性; 教学方法; 教学心得
1 引 言
中学数学教师是以知识点传授为主,非常重视课堂教学,讲究用生动、形象的语言吸引学生,在课堂上可以通过高密度提问,细致分析,反复训练,将知识点讲深讲透,让学生当堂掌握、巩固所学知识点,对概念、理论较少作详细讨论和拓广[1].多年来,很多中学为了追求升学率,老师们大都采用填鸭式教学,搞题海战术,使学生的主观能动性受到压抑,造成高分低能现象.
由此我们首先开展了大学新生对数学分析、高等代数和空间解析几何三门基础课程的学习感受的问卷调查.
2 调查结果
高师院校数学专业的培养目标是致力于培养优秀数学教育实践与研究型人才,使其具备扎实的数学基础,掌握从事数学教学与教学研究的基本方法.通过教育教学类通用课程、数学教学相关知识与方法的学习,使得学生具备从事中职学校、中小学数学教学活动的必要技能与能力;通过计算机和数学软件方面的训练,使学生具备从事相关研究、教学、开发软件等解决实际问题的能力.大学新生刚入学往往会发现《数学分析》、《高等代数》、《空间解析几何》(以下简称为“三基”)这三门课程很难入门,很难与高中所学知识接轨,也很难将三者联系起来,并将其应用到实际问题当中.我们从学生的学习角度和教师的教学角度两方面出发,探索如何在三基课程学习中培养学生的创新能力,为学生创造一个更加有利的氛围和更加适宜的情境.为此,我们首先分别对学校大一、大二学生进行了问卷调查,了解他们的学习情况.本次调查发放问卷140份,回收130份.调查结果中约有85%的学生表示对三门课程的学习感到头疼,少数表示相对轻松.他们中存在的问题主要有:
(i) 部分内容上脱节,不能与高中知识连接;
(ii) 学习方法脱节,发现用高中学习数学的方法来学习大学数学,行不通,不适应大学课程的学习;
(iii) 缺乏实际应用意识.
通过问卷调查,我们归纳出的原因主要有以下几点:
(i) 学生的自学意识不强,仍然停留在高中的填鸭式教学模式当中;
(ii) 学生仍然认为教学是大学老师的主要任务,学习依赖性很强.其结果是教我就学,不教就不学;
(iii) 学生过于热衷于参加课外活动,心气浮躁,难以专心地学习专业课程;
(iv) 很多老师在授课是往往只是纯粹地讲授课本知识,与实际生活脱节,让学生感觉到理论太多,一方面使得学生感到枯燥,另外一方面这些理论一时难以找到应用,使得学生感觉没有什么价值,失去学习的动力.
为解决这些问题,我们对“三基”课程内容思想、联系以及教与学的方法进行研讨.
3 “三基”课程概述
“三基”课程作为大学数学专业学习的基础课程,它们有着举足轻重的作用.因为它们是数学相应专业后继课程,如《常微分方程》、《复变函数》、《实变函数》、《近世代数》(《抽象代数》)、《泛函分析》、《概率论》及《数理统计》等课程的基础,也是学生们首先接触到的三门专业基础课.由于数学学科的抽象性、逻辑性,这就要求学生们在学习数学基础课时脚踏实地,打好基础,注重数学基本功的训练.否则,想学好数学专业的后继课程是很困难的.就比如说,我们目前学习的《近世代数》,就是《高等代数》的后继课程.《高等代数》的解题思想渗透其中,若《高等代数》学习的较好,就可用类比的方法学习《近世代数》,当然就可以取得事半功倍的效果了.
4 “三基”课程的内容及其思想
作为大学数学专业学生,在学习过程中不仅要理解“三基”课程的作用及特点,还要逐步培养数学能力.那么,什么是数学能力呢?所谓数学能力是指表现在掌握数学技能、数学思想方法上的个性心理学特征.其中,数学技能在解题过程中主要体现在探索阶段(即观察、试验、想象、发现)、实施阶段(即推理、运算、表达、实现)和总结阶段(即抽象、概括、总结、成果)[2].而这几个过程包含了创新技能的全部内容.三门课程主要思想归纳如下:
(i) 数学分析
《数学分析》课程主要内容有实数与函数、数列极限、函数极限、一元函数连续、一元函数微分学、微分中值定理及其应用、实数的完备性、不定积分、定积分及其应用、广义积分、数项级数、函数级数、幂级数、傅里叶级数、多元函数的极限与连续、多元函数微分学、隐函数定理及其应用、含参变量积分、二重积分、三重积分、曲线积分、曲面积分[3].该课程的思想主要体现在以下几点:
第一是函数的思想,数学分析课程的研究对象就是函数,重点研究函数的连续性、可微性和可积性.
第二是极限的思想,数学分析课程是以极限为工具来研究初等函数,极限理论贯穿于数学分析全书.
第三是连续的思想,数学分析所研究的函数基本上都是连续的(或者是几乎处处连续的).
(ii) 高等代数
《高等代数》课程的内容主要包括多项式理论、行列式、线性方程组、矩阵和线性空间.高等代数主要起到工具的作用,矩阵的应用在其他学科尤其广泛.化繁为简是其主要思想,初等变换方法贯彻于全书之中.
(iii) 空间解析几何
《空间解析几何》课程主要研究空间(或平面)图形的形状、大小或位置相互关系,是解决数学问题的有力工具.其主要思想是数形结合,几何的问题代数方法来解决.
5 三基课程间的关系
下面通过例题阐明创新技能在解题过程中的应用.另外,它们也充分体现“三基”课程之间的联系.
5.1 数学分析与高等代数的联系
在数学分析与高等代数这两门课程看似彼此相对独立,实际上却是联系紧密的,而且适当运用分析的思想方法解决代数问题,或者应用代数的定理来解决分析问题,往往会收到意想不到的效果.下面就通过实例加以说明:
5.1.1 高等代数中的二次型理论在数学分析解题中的应用

解由于
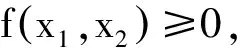
从而证得
本题主要运用了高等代数中的矩阵、行列式及二次型知识来解决数学分析中的不等式问题,过渡自然,衔接紧密,方法新颖.
5.1.2 高等代数中的线性变换理论在数学分析重积分中的应用

V={(x,y,z)|x2+y2+z2≤1}.
本题若利用一般的三重积分计算方法(即化为累次积分)是很难求出结果的,这种方法也是行不通的,但若采用高等代数中的正交变换,则很容易解决,作如下正交变换:


例3计算二重积分
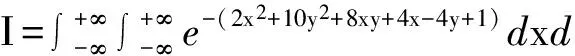
解被积函数的指数部分不是一个实二次型,可以通过坐标变换化为二次型.因为
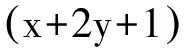
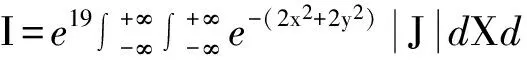

求二重积分是数学分析中的常见题型,本题若要直接求积分将会相当困难,而用换元法结合高等代数中的行列式这个有力工具,则将会达到事半功倍的效果.
5.1.3 高等代数中的相关性理论在数学分析中的应用
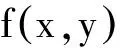
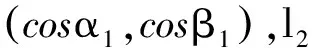
即
而

5.1.4 数学分析中二重积分理论在高等代数中的应用
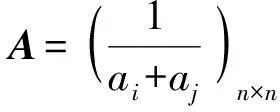
此题若用半正定矩阵判别法直接去证实很难证出的,可改用二重积分的办法来解决,即设X=(x1,x2,…,xn)T,则

上例无论是在题目上还是在解题过程中,分析思想和代数思想都好像是融为一体了.试想在例1解题过程中,用传统的解法计算会有多么复杂,且易出错,更不容易算出最终的线性表示关系.而现在,我们利用矩阵及逆矩阵就可以轻而易举的解出本题,可见创新技能在解题中的优势.
此外,黑塞矩阵对数学分析中条件极值的判定、矩阵的引入对柯西中值定理及拉格朗日中值定理也起到至关重要的作用;数学分析方法在矩阵论中的应用也非常广泛.在这里就不一一举例了.另外,在高等代数中,我们知道欧式空间中的一组非零向量,若它们两两正交就称为正交向量组.在n维欧式空间中,若n个向量组成一个正交向量组,则称该向量组是一个正交基.另外,由单位向量组成的正交基称为标准正交基.对∀α∈n,有
α=a1ε1+a2ε2+…+anεn,
其中ai=(α,εi),(这里(,)是欧式内积).
当我们在华东师范大学版《数学分析》[2]第十五章接触到傅立叶级数时,我们知道:若函数
则它可以看成是由三角函数列(也称三角函数系)
1,cosx,sinx,cos2x,sin2x,…,cosnx,sinnx…
(*)
所产生的一般形式的三角函数.易证,1,cosx,sinx,cos2x,sin2x,…,cosnx,sinnx…是线性无关的,故可作为一组基.即(*)相当于εi(i=1,2,…,n)的作用.利用欧式内积可得
我们的研讨结论是:高等代数中的矩阵、行列式、二次型及线性空间等知识为数学分析的解题提供了有力的工具;反过来,数学分析中分析问题的思想也在很大程度上简化了高等代数的求解.
5.2 空间解析几何与高等代数的联系
高等代数的内容主要有: 多项式、行列式、线性方程组、矩阵、线性空间、线性变换、欧氏空间、λ-矩阵与若当型、二次型.空间解析几何主要研究二维实空间中的直线与二次曲线、三维实空间中的平面与二次曲面、空间曲线和空间曲面的位置关系、平移变换和旋转变换[5].而且空间解析几何课程的中心思想是把代数方程与曲线曲面等图形联系起来,通过代数的方法研究几何问题.由此可以发现两门学科之间联系的很紧密.
在我们刚进入大学时,比较习惯于处理具体的数学问题,对数学的抽象性心理准备不足,因而在学习高等代数常被高等代数中出现的大量抽象概念所困扰,导致对学好高等代数缺乏信心.这个时候空间解析几何就显得非常重要了,因为在高等代数中的许多概念和方法都可在空间解析几何中找到其几何模型,这样就可以把抽象问题具体化,更容易理解.其中我们归纳出以下几点联系:
(i) 几何中的矢量代数与代数中的(n维)向量空间、线性空间、欧氏空间联系密切;
(ii) 几何中的直线、平面方程及线面、面面的位置关系与代数中矩阵的秩及线性方程组联系密切;
(iii) 几何中的坐标变换与代数中的线性变换联系密切;
(iv) 几何中的二次曲线、曲面的化简和分类与代数中的二次型理论联系密切.
这里强调的是,代数是工具,空间解析几何亦是代数的工具,几何为理解代数提供背景材料与应用场所.
5.2.1 空间解析几何中的旋转变换理论在高等代数计算中的应用
比如下面这个经典例题:
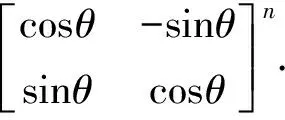
正常的计算方法是通过代数中的纯矩阵运算处理,先计算
由归纳法,得出
T:2→2∶(x,y)→(xcosθ-ysinθ,xsinθ+ycosθ),

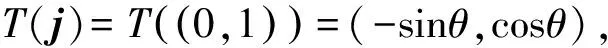
求得线性变换T在该基下的矩阵为
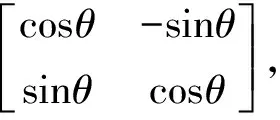
则题目中所求的
可以看成是线性变换T的n次幂,即Tn在2中自然基下的矩阵;而Tn在几何上看就是平面按逆时针方向绕原点旋转n个θ角即nθ角的线性变换,故Tn在自然基下的矩阵就是

因此,有
5.2.2 高等代数中的二次型理论在空间解析几何求解二次曲线中的应用
例7当坐标原点与中心重合时,一个有心二次曲线的一般方程为:
ax2+2by+cy2=f.
(1)
为了便于研究这个二次曲线的几何性质,我们可以选择适当的角度θ,作转轴
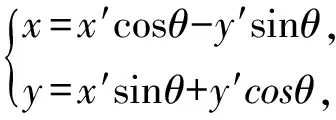
(2)
把方程(1)化成标准方程.
显然,方程(1)的左端是一个二次齐次多项式.从代数的观点来看,所谓的化标准方程就是用线性替换(2)对一个二次齐次多项式进行化简,使其只含有平方项,不再含有交叉项.这种方法可以推广到n元二次齐次多项式的情形,即《高等代数》中的二次型的研究.
例8设P是一个数域,一个系数为数域P上的x1,x2,…,xn的二次齐次多项式
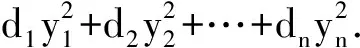

(a) 当d1,d2,d3均大于0(三正)时,


x2+y2=1 在空间中为旋转柱面,
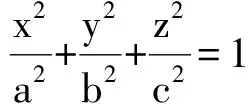
(b) 当d1>0,d2>0,d3<0(两正一负)时,
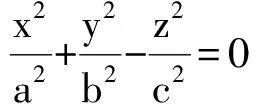

(c) 当d1>0,d2<0,d3<0(一正两负)时,

高等代数中的二次型与空间解析几何中的二次曲线有着千丝万缕的联系.二次曲线的标准方程为标准二次型的几种特殊情况.我们也发现,二次曲线是在有限空间中存在,而标准二次型是在无限维空间中的,它们之间在这一点上有差异.
另外,利用线性方程组解的理论去判定几何空间中的线线、线面、面面之间的关系等,也反映了这两个学科之间的紧密联系.
通过总结归纳和反思,我们对这组的研讨结果是:空间解析几何的坐标系的建立及各种变换(线性坐标变换、平面旋转变换等)为高等代数提供了数形结合的基础,高等代数又为空间解析几何中提供有力的计算工具.但在实际应用中,同学们普遍反映的问题是:空间解析几何知识点太多太碎,要达到灵活运用的程度还是有一定难度的.
5.3 数学分析与空间解析几何的联系
5.3.1 空间解析几何在引入数学分析概念中的作用
对于刚刚进入大学的大一新生来说,由于高中的数学思维基本上是直观的思维,一下从概念性的抽象思维来引入、建立数学分析中的系列抽象概念是有一定困难的.如果能够从客观现实背景出发,通过几何直观,则容易克服入门难问题.
例如,数列极限的概念是数学分析课程学生所遇到的第一个抽象知识点,也是第一个难点.通常的处理方法是借助数轴把数列的变化趋势在数轴上直观展现,观察各类数列的变化趋势,经过形象思维,抽象概括其共有的本质属性,从而给出数列极限的描述性定义,进而定量刻画,便容易上升为精确定义.
莱布尼兹通过求曲线y=f(x)在点x0的切线的斜率的几何方法,抽象概括得出一般函数的导数概念.而牛顿则从求变速直线运动的质点在某一时刻的瞬时速度的角度,抽象概括得出一般函数导数的概念.笔者通过多年的教学发现数学专业的学生更容易理解和接受从求曲线切线斜率抽象出导数概念这种模式.因此,把莱布尼兹的例子放在前面,从求割线斜率演示变化到求切线斜率,再到导数,这种方法比较自然、生动,教学效果好.至于不定积分的概念的引入,则以求导问题的逆问题为切入点,然后通过结合直观(画函数图像),明确原函数族的几何意义.对于定积分的概念引入时,一般均以计算曲边梯形的面积为例,这也是形象思维的好材料,同样对于二重积分的引入,采用求曲顶柱体的体积的例子,也是充分体现几何直观的思想.所以数学分析中的抽象概念若能够利用几何的直观思维来理解,则学生的学习效果会非常的好.
5.3.2 空间解析几何在数学分析论证中的作用
5.3.2.1 零点定理[6]
若函数f(x)在闭区间[a,b]上连续,且f(a)f(b)<0,则在开区间(a,b)内至少存在一点c使得f(c)=0.
该定理的证明方法一般是利用闭区间套定理[6],其主要的思想是构造一系列的区间,通过区间的逐步缩短,从而“套出”f(x)的零点,这思想体现了几何直观.另一种几何直观方法是寻找连续函数f(x)在闭区间[a,b]上的首个零点或最后一个零点,直观的要点是把握这些零点的几何性质.闭区间上连续函数的零点均是函数值取正负的分界点.比如果设f(b)>0,那么由连续函数零点的几何性性质,构造集合E={x∈[a,b]|f(x)>0},令α=infE,然后由下确界的定义就可以证明f(α)=0,当然上述集合E的构造可以是多种多样的.这种几何直观所诱导的证明思路可将繁长的证明化为一幅易于掌握的几何图形,降低了证明的难度,易于学生掌握定理的本质.

图1
5.3.2.2 介值性定理[6]
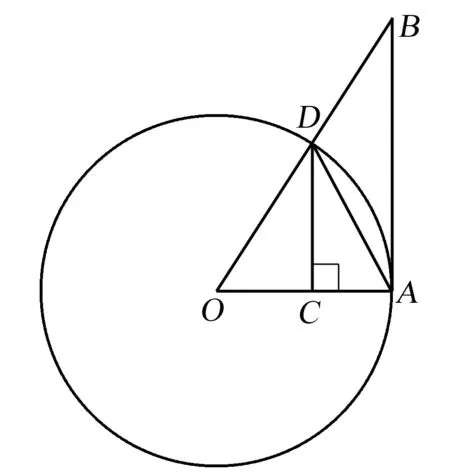
设函数f在闭区间[a,b]上连续,且f(a)≠f(b),若μ为介于f(a)与f(b)之间的任何实数(f(a)<μ f(x0)=μ. 这个定理表明,若f(x)在[a,b]上连续,又不妨设f(a) [f(a),f(b)]⊂f([a,b]). 这种通过几何图1直观形象地理解定理的内容使得学生更容易理解和掌握定理内容的实质,然后才能够准确地运用该定理,达到了化抽象为形象的目的. 5.3.2.3 反函数的求导法则 若函数f(x)在x0的某邻域上连续且严格单调,y=f(x)在x0可导且f′(x0)≠0,则它的反函数x=ψ(y)在y0=f(x0)可导且 以上定理的证明是较为简单的,因为它仅仅涉及到导数的概念及反函数的连续性定理.但问题是学生对反函数的求导公式没有直观的印象.鉴于此,我们可以观察它的较为明显的几何意义,即若以α和β分别表示曲线y=f(x)在点(x0,f(x0))的切线与x轴正向的夹角和曲线在x=ψ(y)点(x0,f(x0))的切线与y轴正向的夹角,那么α+β=π±π/2,于是tan(α)tan(β)=1,即ψ′(y0)f′(x0)=1,故 而要求f′(x0)≠0也是自然的,否则曲线y=f(x)在点(x0,f(x0))的切线与x轴平行,于是曲线x=ψ(y)在点(x0,f(x0))的切线就与y轴垂直,从而函数x=ψ(y)在f(x0)不存在导数. 5.3.3 空间解析几何在数学分析解题中的应用 有些题目,借助几何直观,可以突破解题的关键思路.而有些题目首先借助于图解法分析,进一步地用数量关系的解法加以验证,这样会加深学生理解.下面对书上的例题进行举例说明. 证先分析它的几何意义,这样对于整体上把握证题思路、写出逻辑证明是大有帮助的. 在空间解析几何中,我们经常遇到各种立体模型.它们的出现强化了我们的空间想象能力,也为我们解决数学分析问题提供了直观的模型. 例10对于双曲抛物面 它被xOy平面分割成上下两部分,上部分沿x轴的两个方向上升,下部分沿y轴的两个方向下降,曲面的大体形状像一个马鞍.所以双曲抛物面也叫做马鞍曲面.如图2所示. 图2 在《数学分析》中,涉及到多元函数,如:z=xy是定义在xOy平面上的函数.乍一看这个二元函数与马鞍曲线没有关系,如果对于 图3 当x<0时,由sin(-x)<-x得sin(-x)<-x 综上,又得到不等式 通过此题更让我们觉得几何图形对于数学分析的解题具有不可忽视的作用,如果只是凭空想象我们很难发现sinx与x以及tanx之间的关系,进而对于本题就无法进行下去,所以空间解析几何不仅能让初学者对数学分析的抽象概念更好地理解,它也是数学分析解题的有力工具. 此外,我们也可利用数学分析的知识来解决空间解析几何中的问题.比如用隐函数定理的知识来解决求平面曲线的切线与法线、空间曲线的切线与法平面、曲面的切平面与法线等问题.用数学分析中定积分的知识来求解平面图形的面积、平面曲线的弧长与曲率、旋转曲面的面积等问题.我们从中可以发现数学分析与空间解析几何相互渗透,两者的融合加深了我们对这两科知识的理解和掌握.下面我们将举出几个数学分析在解决几何问题中的作用的实例. 5.3.4 数学分析在空间解析几何解题中的应用 特别地,当x1=-R,x2=R时,则得球的表面积S球=4πR2. 对于这个从中学我们就熟知的公式我们都很好奇它是怎么得来的,但一直由于知识有限不能证明,而今通过数学分析的学习,我们懂得了它的原始意义.所以,数学分析通过精确的论证让我们更清楚地掌握了空间解析几何中一些大家认为理所当然的知识.初中时我们就学过怎样求解一些平面曲线的切线方程,那么关于空间曲线的切线方程我们该如何求解呢?数学分析中偏导的学习为我们接开了空间解析几何的又一层面纱.比如下面这个例子: 即 由此可见,数学分析在空间解析几何中的作用也不可否认.空间解析几何知识为数学分析提供直观的图形处理方法,使其能够更好地发挥数形结合思想的作用.反之,数学分析中的极限思想和微积分思想也在很大程度上为几何寻找新的思路及有力的支撑.另外,空间解析几何的学习让我们都更好地通过形象的图形理解抽象的概念更轻松的发现数学的理与美,相信也一定会增强我们的数学技能.但在实际学习应用中,同学们普遍反映:很难系统的把握空间解析几何知识,比较零散;数学分析的学习也只是停留在基本概念上;学习没有兴趣,无法进行主动积极的思考. 5.4 数学分析、高等代数、空间解析几何三者相互渗透 由以上讨论,我们可以看出“三基”课程之间两两联系紧密,当然会令人自然想问,三者是不是有联系呢?答案是肯定的.例如,在例13中,就将高等代数中的行列式(雅克比行列式)、数学分析中的微分及隐函数及空间解析几何中的求基本平面方程的求解联系起来,表现出“三基”课程之间的互通性与关联性. 通过研讨,我们惊奇的发现,《数学分析》、《高等代数》、《空间解析几何》在许多方面有互通之处,它们在很大程度上揭示了数学的美. 我们知道事物之间是普遍联系的,我们不能孤立的看问题.作为初学者或许会感觉《数学分析》、《高等代数》、《空间解析几何》之间没有什么联系,现在看来那样的想法是不合理的. 在整个大学期间,立足于培养扎实的数学基础.曾有人说过:从人才的培养角度来讲,一个学生能否学好数学,很大程度上决定于他进入大学伊始能否将《数学分析》这门课真正学到手.而我们说,不仅要学好《数学分析》,还要学好《高等代数》和《空间解析几何》.通过“三基”课程的学习,培养学生严密的逻辑思维能力、推理能力及娴熟的运算能力,拓宽知识面,具备创新意识、开拓精神和运用能力,只有具有了这样的条件才算是符合新世纪要求的优秀人才. “三基”课程是大一新生普遍反映难学的三门课程.这三门课程的共同特点就是逻辑性强,比较抽象,内容上与高中相比有一定的跳跃性.若想学好它们,就要注意这三门课程内在关系的联系,把握好理解与记忆的关系. 通过调查,我们发现了同学们在学习中普遍存在的问题,并对其原因展开深入地研讨后得出结论,具有代表性.然后集思广益,通过查阅大量的图书资料,对大家的学习心得的总结进行了综合并研讨,总结出“三基”课程的联系. [1] 盛兴平,王海坤.新课标下高师数学分析教学实践与研究[J].大学数学,2013,29(1):11-14. [2] 王朝晖.关于中学生数学推理能力及其培养的研究[D].华中师范大学, 2000. [3] 金玲玉,许少梅,刘文琰.数学分析教学改革的几点认识和体会[J].大学数学,2012,28(4):25-30. [4] 北京大学数学系几何与代数教研室.高等代数[M].北京:高等教育出版社, 2003. [5] 吕林根,许子道.空间解析几何[M].北京:高等教育出版社,2010. [6] 华东师范大学数学系.数学分析[M].北京:高等教育出版社,2010. Research and Discussion on Associative Teaching of Three Basic Curriculum For Mathematics in Normal College SHENGXing-ping,TANGJian,XINDa-wei,XUChuan-you (School of Mathematics and Statistics, Fuyang Normal College, Fuyang Anhui 236037,China) Students of mathematics in normal universities, they firstly face to study three basic curriculum — “mathematical analysis”,“advanced algebra” and “ space analytic geometry”.This article mainly study intrinsic relations of three basic curriculum from its content, teaching, and the skills of problem solving.Then we can further promote the teaching reform of three basic curriculum. three basic curriculum; correlation; teaching method; teaching experience 2016-05-03; [修改日期] 2016-06-24 安徽省省级教学团队(2015jxtd023),安徽省省级精品资源共享课程(2015gxk041)和基层组织优秀教研室(2013JCJS03) 盛兴平(1976-),男,博士,教授,从事数值代数研究.Email:xingpingsheng@163.com G642 C 1672-1454(2016)06-0106-11
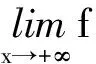




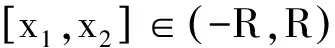

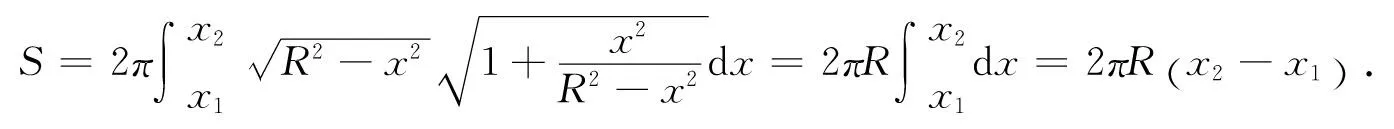



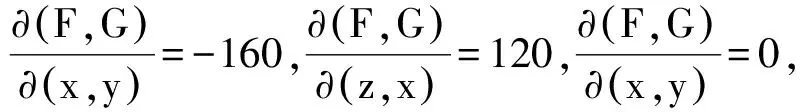
6 总 结

