基于计算思维培养的离散数学课程教学研究
武建春
(内蒙古师范大学计算机与信息工程学院,呼和浩特010022)
基于计算思维培养的离散数学课程教学研究
武建春
(内蒙古师范大学计算机与信息工程学院,呼和浩特010022)
计算思维是当前计算机教育中的研究热点.从计算思维的角度重新审视离散数学课程,梳理各部分内容所蕴含的计算思维基本方法,提出教学过程要以抽象和自动化为核心思想,增加实践教学内容,从而加强计算思维的培养.提出计算思维的培养应该在课程考核中有所体现.
计算思维; 离散数学; 教学; 抽象; 自动化
1 引 言
从2006年计算思维(computational thinking)概念[1]的提出,到如今计算思维的培养成为计算机专业的教育目标之一已经10年了.在这10年里,国内计算机教育工作者对计算思维培养的研究取得了一定成果,但尚未形成一套完整的方法体系,仍处于小规模、探索性阶段.如何在教学过程中培养计算思维,还有许多尚待探索的问题.本文从计算思维的角度梳理离散数学与计算思维之间的内在联系,重新组织教学内容,增加教学实践环节,探索研究离散数学教学中计算思维的培养.
2 计算思维
计算思维是运用计算机科学的思想与方法进行问题求解、系统设计、人类行为理解等涵盖计算机科学之广度的一系列思维活动[1].计算思维的本质是抽象(Abstraction)和自动化(Automation)[1].抽象的特征源自数学思维,但与数学的抽象化有不同的含义,其抽象化不仅表现为形式化表示,同时这种表示应具备有限性、程序性和机械性[2].计算思维又源自工程思维,是数学思维和工程思维的互补与融合.计算思维方法是约简、转化、仿真、递归、并行、抽象、分解、建模、冗余、容错、纠错、规划、学习和调度、折衷等.因此,计算思维是求解问题的一条途径,是一种技能,也是思想[3].
2010年《高等学校计算机科学与技术专业人才专业能力构成与培养》中指出计算思维能力主要包括问题及问题求解过程中的符号表示、逻辑思维与抽象思维、形式化证明、建立模型、实现类计算和模型计算、利用计算机计算等[4].其过程实现就是先根据实际问题构建数学模型,之后把构建的数学模型转化为算法和程序编码,最后在计算机上测试、获得正确的运行程序并求解.
3 离散数学教学与计算思维的培养
离散数学是计算机科学与技术专业的核心理论基础课,它研究的对象是离散量的结构及其相互关系,主要用于计算机系统及其应用领域的建模及分析.因此,离散数学的教学目标就是学生能够运用离散结构构建问题的抽象模型、并在其基础上具有构造算法和解决问题的能力[5].这恰好体现了计算思维中的抽象和自动化两个核心思想,或者说计算思维已融入离散数学的整个知识体系.由此,计算思维提供了一种重新审视离散数学的视角,提供了一种改革离散数学教学内容和教学模式的新思路.
3.1 理论教学中计算思维的培养
离散数学由数理逻辑、集合论、代数结构和图论等多个彼此相互独立的数学分支组成.教学过程突出问题之一是:学生感到离散数学内容庞杂,每部分内容彼此联系不大,留下知识零散的印象.
尽管离散数学包含的内容多,但每部分内容的共同特点是
(i) 以字母、符号或图形等形式呈现的大量、抽象的离散量(抽象概念);
(ii) 不同离散量相应的研究方法;
(iii) 抽象和自动化贯穿始终.教师组织教学内容时,关键要以抽象和自动化为主线,讲清楚各部分内容之间的内在联系.通过教师的具体讲授,让学生从抽象和自动化的角度去认识和理解离散数学课程的各部分内容,摸清它们之间联系的脉络,认识到各部分内容是一个有机的知识整体.实际上,集合论、数理逻辑和图论从抽象角度都可以理解为一种具体的代数系统.同时,在教学过程中教师要提炼并展现隐藏于知识背后计算思维的基本方法,有意识地强化学生对思想方法的理解和掌握.也就是说,计算思维方法是要明确讲出来的、并逐渐内化为学生的思维方法.
3.1.1 数理逻辑的核心是用数学方法来模拟人们思维中的逻辑推理过程.也就是把推理过程像数学一样利用公式来描述.因此,数理逻辑强调的是抽象和形式化.从计算思维的角度重新梳理数理逻辑教学内容(表1),尽可能地提炼每个知识点中关于计算思维的基本方法,把计算思维融入到教学之中.

表1 数理逻辑部分各知识点对应的计算思维方法
上表的知识点充分体现了计算思维中抽象、建模、形式化、推理、规约等基本思维方式.数理逻辑的符号化部分体现了计算思维的抽象性;公式和逻辑推理部分包含了计算思维的自动化思想,可以用程序自动化完成;归结推理方法用算法实现.
3.1.2 图论是描述事务之间关系的工具.这部分内容概念多、方法应用广.学习过程中有两种倾向:一部分学生面对大量的图的基本概念、定理及其方法不知所措,感到困惑;少部分学生抽象、分析能力强,潜意识具有计算思维,运用类比、归纳等方法学习起来得心应手.
图论内容的产生,例如图结构、树结构等被明确提出来,可以说是计算思维的结果.而这些内容本身也清晰化了计算思维的具体形式和表达方式.因而,有意识强化学生计算思维能力,对于学生知识的理解和掌握是十分必要的.首先让学生充分理解“图”这一离散结构,认识到它不同于欧氏几何中的图,与线的长短曲直、角度的大小等无关,只与事物之间的联系有关,是一种特殊的数学符号.欧拉图、哈密尔顿图就是欧拉七桥问题、环球旅游问题经过抽象构建的典型的图模型.其次,在图的基本概念基础上,以经典案例为基础,比如中国邮路问题、货郎担问题,引导学生对实际问题进行抽象和分析,构建所涉及的计算原理并解决问题.在实例应用中获得知识,提高计算思维能力(如表2).
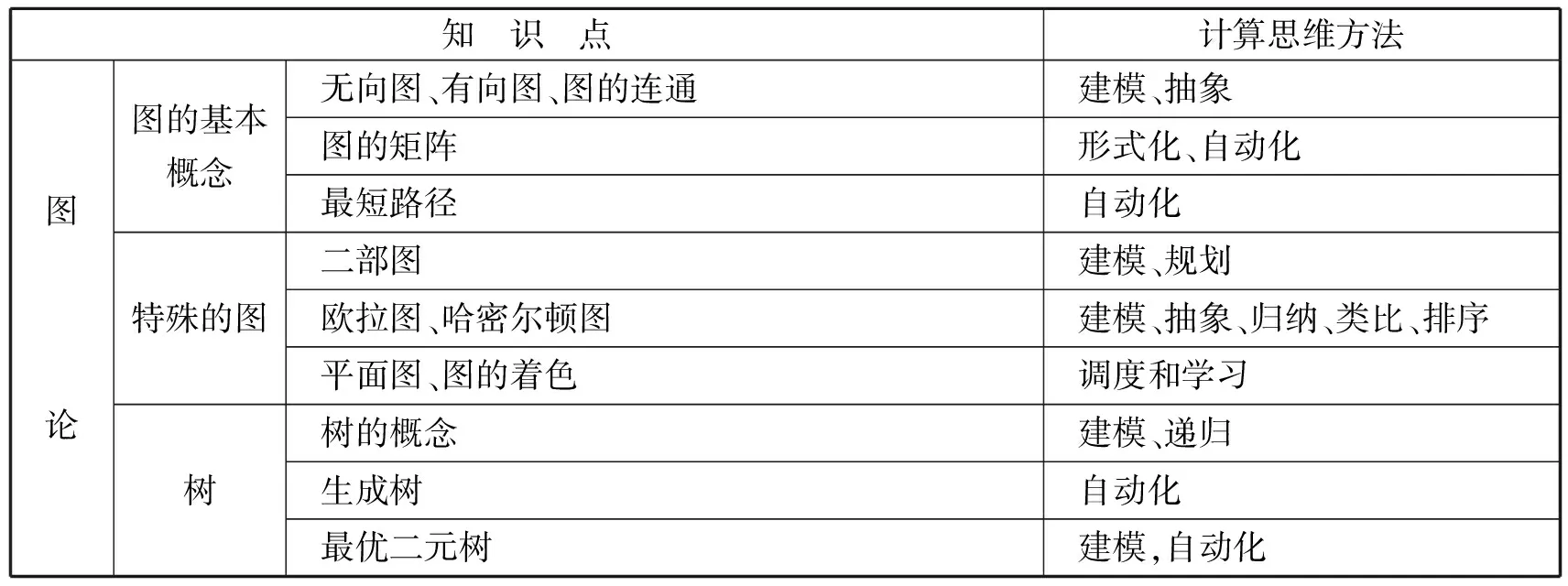
表2 图论部分各知识点对应的计算思维方法
3.1.3 集合是构造离散数学的基础,关系是特殊的集合,函数又是一种特殊的关系.表3梳理了集合论各知识点内容中对应的计算思维基本方法.

表3 集合论部分各知识点对应的计算思维方法
代数系统内容各知识点对应的计算思维方法主要是建模、抽象、形式化和自动化.
教师从计算思维的角度组织教学内容,运用案例教学法、问题导入法、任务驱动法等行之有效的教学方法实施教学,让学生学会用抽象和自动化的思维方法去分析问题、解决问题.
3.2 实践教学中计算思维的培养
教学过程突出问题之二是:教学以讲授理论知识为主,缺少实践应用.因此,学生往往将其作为一门数学课程学习,对理论知识的理解只停留在抽象阶段,很难将理论知识与实际应用联系起来,难以体会该课程与计算机科学之间的联系.
计算思维理念的核心是以抽象和自动化为手段进行问题求解和系统实现,这也是离散数学的教学目标.自动化就是将复杂问题通过逐步计算、求解,找到解决问题的算法,利用计算机实现[6].自动化隐含了需要某类计算机(机器或人)去解释抽象,是抽象的具体化、程序化和机械化.所以,适当增加实验教学,选取重要概念、性质、方法转变成算法用程序实现(如表4),既使学生实际感受和体验知识产生过程,又有利于学生对理论知识的认识和掌握,使自动化思想在教学过程中得以充分体现.

表4 离散数学实验内容举例
由于课时的限制,编程自动化实现的内容以小组形式按以下步骤可以让学生课外完成
(i) 布置实验任务.可以是基本概念、性质或计算方法的基础性实验,也可以是需要分解成多个子任务的综合性实验;
(ii) 对任务分析讨论,明确任务所涉及的知识点,收集相关学习资料;
(iii) 找到解决问题的方法,合理分工,制定实验实施步骤;
(iv) 完成实验任务,提交实验报告.
作为课外实践要求,让学生实际感受问题解决过程,从而学生对课程的理解也不会仅仅停留在理论抽象阶段,初步体会离散数学与计算机科学之间的联系,有利于学生增强学习兴趣、提高综合解决问题能力.
4 重视计算思维能力的考核
基于计算思维培养的教学过程,在教学考核内容和方式上应有所体现计算思维能力培养的结果.考核内容不仅仅是课堂教学要求的知识点和计算推演,应该增加计算思维相关概念和运用它们解决问题的内容.例如,“楼梯有一盏灯由上下2个开关控制,要求按动任何一个开关都能打开或关闭灯,试设计这样一个线路.”考核学生是否会运用建模、抽象、化简等计算思维方法和命题逻辑的知识解决实际问题.此外,把课下实验内容以实验报告的形式记录成绩,形成“过程性考核+终结性考核+实验报告”综合评价体系,既把握过程又重视计算思维培养结果,也调动了学生学习积极性.
5 结 语
计算思维的培养对离散数学的教学提出了新的要求,为离散数学的教学提供了一种新思路.同时,离散数学课程也为培养学生的计算思维提供了一个很好的平台.计算思维能力是抽象思维能力、逻辑推理能力和解决问题能力的综合体现,是一种创新能力.通过离散数学课程的教学提高学生的计算思维能力,尚需要教师在教学实践中不断地探索和实践.
[1] 周以真.计算思维[J].中国计算机学会通讯,2007,3(11):83-85.
[2] 李廉.计算思维——概念与挑战[J].中国大学教学,2012(1):7-12.
[3] 陈国良,董胜荣.计算思维与大学计算机基础教育[J].中国大学教学,2011(1):7-11.
[4] 教育部高等学校计算机科学与技术教学指导委员会.高等学校计算机科学与技术专业人才专业能力构成与培养[M].北京:北京机械工业出版社,2010.
[5] 常亮,徐周波,古天龙,等.离散数学教学中的计算思维培养[J].计算机教育,2011(14):90-94.
[6] 马艳芳,陈亮.计算思维在离散数学中的应用[J].湖州师范学院学报,2015,37(2):104-107.
The Discrete Mathematics Course Teaching Research Basing on the Training of Computational Thinking
WUJian-chun
(College of Computer and Information Engineering,Inner Mongolia Normal University,Hohhot 010022,China)
Computational Thinking is a hot research topic in computer education.From the view of computational thinking this paper re-examined the discrete mathematics course and combed each substance about the fundamental methods of computational thinking, proposed that abstraction and automation should be the core idea in the process of teaching which should add more practical contents in order to improve the cultivation of computational thinking.The paper pointed out that the training of computational thinking should be reflected in the course assessment.
computational thinking; discrete mathematics; teaching; abstraction; automation
2016-09-08; [修改日期]2016-10-23
武建春(1969-),女,硕士,副教授,从事数学教学和数学教育研究.Email:wujianchun813@126.com
O158
C
1672-1454(2016)06-0075-04

