从Zygmund型空间到Bloch-Orlicz空间上的Volterra型算子的有界性和紧性

王泽灯,徐辉明

(浙江师范大学 数理与信息工程学院，浙江 金华 321004)

从Zygmund型空间到Bloch-Orlicz空间上的Volterra型算子的有界性和紧性

王泽灯,徐辉明*

(浙江师范大学 数理与信息工程学院，浙江 金华 321004)

利用分析和构造检验函数的方法,研究了从Zygmund型空间到Bloch-Orlicz空间上的Volterra型算子的有界性和紧性,并得到了Volterra型算子是从Zygmund型空间到Bloch-Orlicz空间上的有界算子、紧算子的充要条件。

Zygmund型空间; Bloch-Orlicz空间; Volterra型算子; 有界性; 紧性

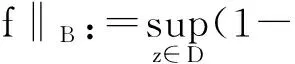
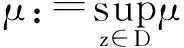
设0<α<∞，定义Zygmund型空间(记作Zα)如下：

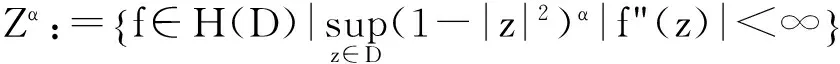
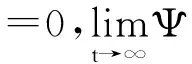
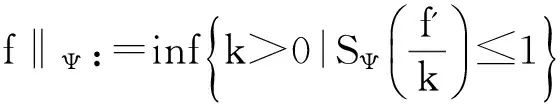
不难验证，‖f‖Ψ是BΨ的半范数，‖f‖BΨ:=|f(0)|+‖f‖Ψ是BΨ的范数，且在该范数下，BΨ是Banach空间。

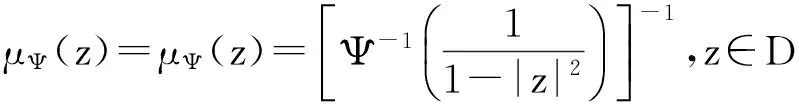
设g∈H(D)，定义H(D)上的Volterra积分型算子Ig和Jg如下：

Igf(z):=∫f'(ζ)g(ζ)dζ，z∈D；

Jgf(z):∫f'(ζ)g'(ζ)dζ，z∈D。

目前，关于Volterra积分型算子Ig和Jg的研究已经取得了丰富的成果，例如在文献[2]中研究了Zygmund空间中算子Ig和Jg的有界性和紧性，并得到了在Zygmund空间中Ig和Jg是有界算子和紧算子的充要条件。

本文研究算子Ig(Jg):Zα→BΨ的有界性和紧性。

1 预备引理

我们需要下面的几个引理。

引理1[3]设f∈Zα，α>0，那么以下命题成立：

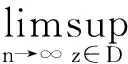
在本文中字母C和L均代表正的常数，在不同的地方代表的值可能不同。

2 算子Ig的研究

对于算子Ig:Zα→BΨ的有界性和紧性，有以下结论。

定理1 设0<α<∞，g∈H(D)，则

(i)当0<α<1时，算子Ig:Zα→BΨ有界当且仅当

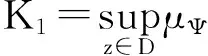
(ii) 算子Ig:Z→BΨ有界当且仅当

(iii) 当α>1时，算子Ig:Zα→BΨ有界当且仅当

证明必要性

假设算子Ig:Zα→BΨ有界

(i) 当0<α<1时，取函数f(z)=z，z∈D.显然‖f‖zα=1

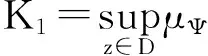
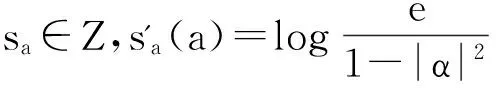
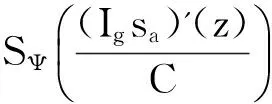
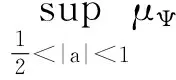
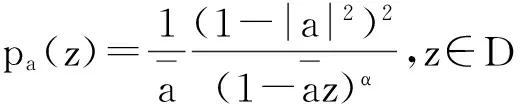
充分性

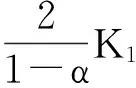
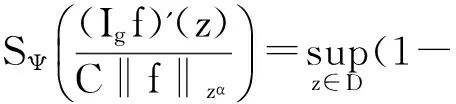
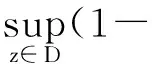
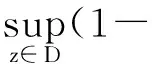
所以‖Igf‖Ψ≤C‖f‖zα，进而‖Igf‖BΨ≤C‖f‖zα，

即算子Ig:Zα→BΨ有界

(ii)和(iii)的证明与(i)类似

定理2 设0<α<∞，g∈H(D)，算子Ig:Zα→BΨ是有界算子，则

(i) 当0<α<1时，Ig是紧算子；

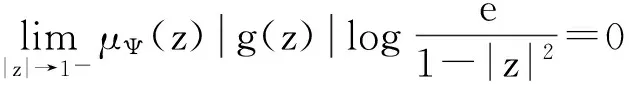
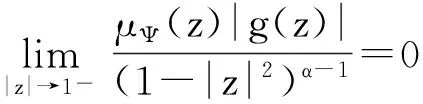
证明

(i)设0<α<1，在Zα中任取在D上内闭一致收敛于0的有界函数列{fn}，

则由Ig的有界性和定理1得

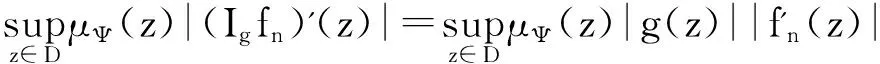
(ii)的必要性

设Ig:Z→BΨ是紧算子，{zn}为D中任意满足条件zn→1(n→∞)的序列，

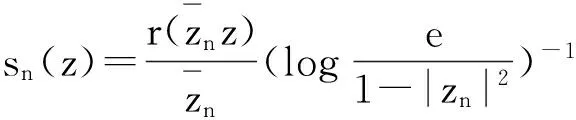
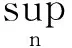
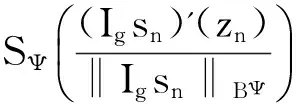
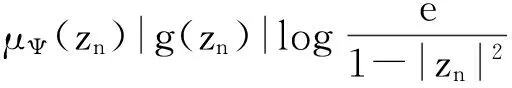
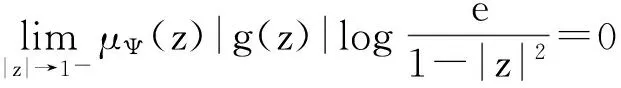
(iii)的必要性

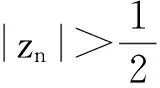
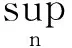
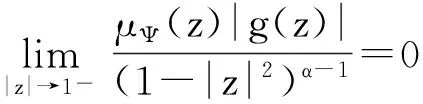
(ii)的充分性

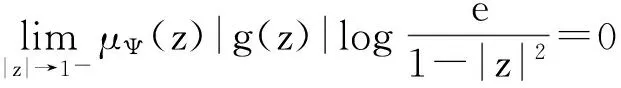
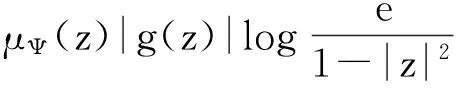
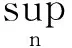
令K={z∈D:|z|≤δ}，根据引理1得

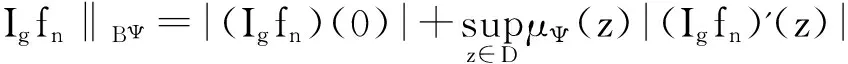
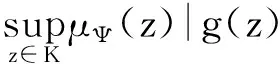
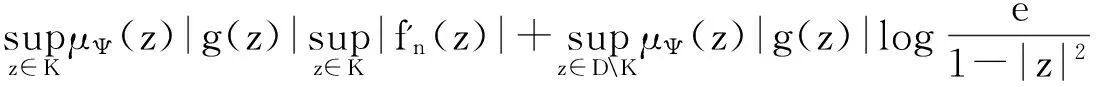
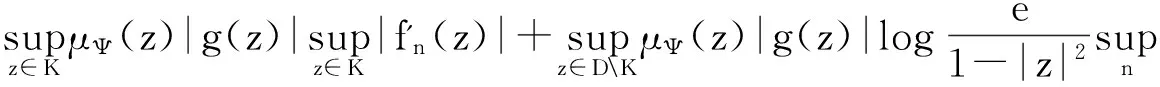
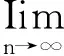
由引理2知算子Ig:Z→BΨ是紧算子.

(iii)的充分性

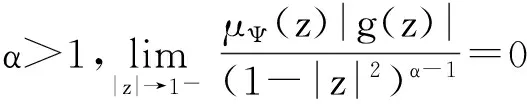
在Zα中任取在上D内闭一致收敛于0的有界函数列{fn}，

类似于上面的证明过程，结合定理1和引理1可得

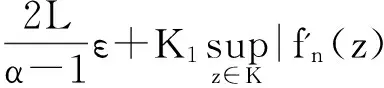
3 算子Jg的研究

对于算子Jg:Zα→BΨ的有界性和紧性，有以下结论。

定理3设0<α<∞，g∈H(D)，则

(i) 当0<α<2时，算子Jg:Zα→BΨ有界当且仅当

(ii) 算子Jg:Z2→BΨ有界当且仅当

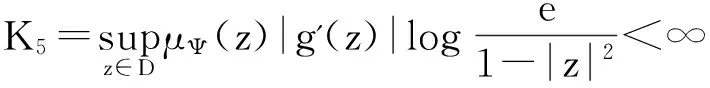
(iii) 当α>2时，算子Jg:Zα→BΨ有界当且仅当

证明 必要性

(i) 设当0<α<2时，算子Jg:Zα→BΨ有界

取函数f(z)=1，显然‖f‖Zα=1

故存在常数C>0，使得

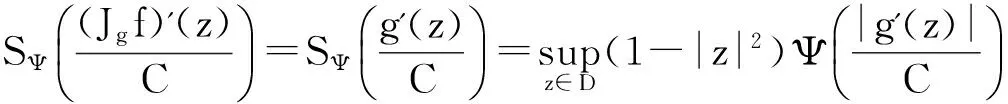
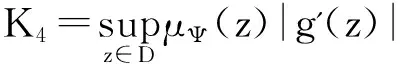
(ii) 设算子Jg:Z2→B有界对于任意固定的a∈D，作函数

易知sa∈Z2由Jg的有界性，存在常数C>0，使得‖Jgsa‖BΨ≤C，

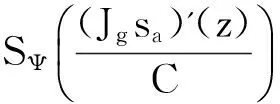
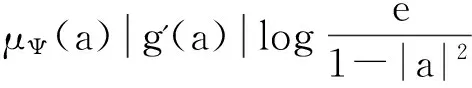
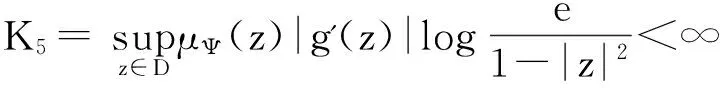
(iii) 设α>2，算子Jg:Zα→BΨ有界对于任意固定的a∈D，作函数

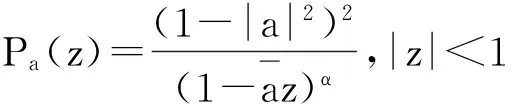
易知Pa∈Zα，类似于(ii)的证明可得

充分性

(i)设0<α<2，由引理1知，存在常数C(α)>0，对任意f∈Za{0}有

|f(z)|≤C(α)‖f‖za

取常数C≥K4C(α)，则有

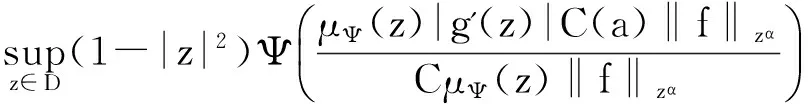
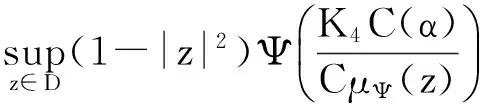
所以‖Jgf‖Ψ≤C‖f‖zα

进而，‖Jgf‖BΨ≤C‖f‖zα

因此算子Jg:Zα→BΨ有界

利用引理1，类似于上面的方法可以证明(ii)和(iii)的充分性

对于算子Jg:Zα→BΨ的紧性，我们有

定理4设0<∂<∞，g∈H(D)，算子Jg:Zα→BΨ是有界算子，则

(i) 当0<∂<2时，Jg是紧算子；

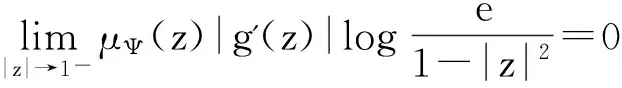
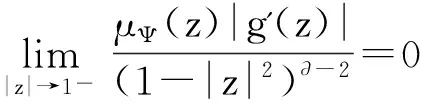
证明

类似于定理2的证明，

当α=2时，取函数列

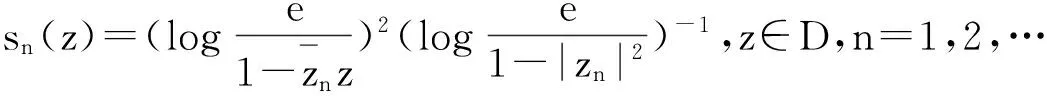
[1]RAMOS-FERNANDEZ J C. Composition operators on Bloch-Orlicz type spaces[J]. Applied Mathematics and Computation, 2010, 217(7): 3392-3402.

[2]LI Song-xiao, STEVIC S. Volterra-Type operators on Zygmund spaces[J]. Journal of Inequalities and Applications, 2007(1): 30C80.

[3]LI Hai-ying, GUO Zhi-tao. On a product-type operator from Zygmund-type spaces to Bloch-Orlicz spaces[J]. Journal of Inequalities and Applications, 2015(1): 37-51.

[4]COWEN C C, MACCLUER B D. Composition operators on spaces of analytic functions[M]. boca roton: crc press, 1995.

[5]STEVIC S. On an Integral-Type operator from Zygmund-Type spaces to Mixed-Norm spaces on the unit ball[J]. Abstract and Applied Analysis, 2010, 215(11): 3817-3823.

[6]LI Song-xiao, STEVIC S. On an integral-type operator from omega-Bloch spaces to mu-Zygmund spaces[J]. Applied Mathematics and Computation, 2010, 215(12): 4385-4391.

[7]STEVIC S. On new Bloch-type spaces[J]. Applied Mathematics and Computation, 2009, 215(2): 841-849.

[8]ZHU Xiang-ling. Generalized weighted composition operators on Bloch-type spaces[J]. Journal of Inequalities and Applications, 2015(1): 107-119.

[9]JIANG Zhi-jie. On Stevic-Sharma operator from the Zygmund space to the Bloch-Orlicz space[J]. Advances in Difference Equations, 2015(1): 1-16.

[10]JIAN M, RUAN J-c. The cauchy integral operator on weighted hardy space[J]. 数学年刊B辑(英文版), 2010, 31(4): 461-472.

(责任编辑：马世堂)

The Boundedness and Compactness of Volterra-type Operatorsfrom the Zygmund-type Spaces to the Bloch-Orlicz Spaces

WANG Ze-deng,XU Hui-ming*

(Mathematics and Information Engineering College,Zhejiang Normal University, Jinhua 321004, China)

By using analysis methods and constructing test functions, the boundedness and compactness of the Volterra-type operators from the Zygmund-type spaces to the Bloch-Orlicz spaces are investigated. Then the sufficient and necessary conditons of boundedness and compactness of the Volterra-type operators are obtained.

Zygmund-type spaces; Bloch-Orlicz spaces; Volterra-type operators; Boundedness; Compactness

2016-01-06

国家自然科学基金(11271124,11271332); 浙江省自然科学基金(LY14A010013,LY16A010004)。

王泽灯(1992-)，男，浙江省义乌市人，在读硕士研究生，主要从事函数空间及其算子理论研究。*通讯作者：徐辉明，教授，E-mail: xhm@zjnu.cn。

O174.56, O177.2

A

1673-8772(2016)06-0064-07