浅析高中数学教材资源的合理深化
冒志红
摘 要:数学教材中对教学内容进行了明确罗列,这是教师开展教学活动的大纲性依据。我们要创造性地深化使用教材,深化概念理解,筑牢知识基础;深化内容把握,鼓励变式思维;深化规律总结,寻找共性方法;深化学以致用,勤于联系实际。
关键词:高中数学 教材资源 合理深化
数学是持续变化的,更是灵活变化的。对于数学问题的思考与研究永远没有止境。如果说,小学和初中阶段的学习是在为学生的数学探究之路奠基的话,那么,高中阶段的数学学习就是带领学生真正走进了这个多元多变的知识殿堂。进入高中数学学习,很多学生都表现出了对知识接受的不适应,感到有太多难以把控的东西,无法将其全面掌握。这就是数学学科灵活变化与深入的具体表现。对于此类现象,如果教师没有发现或熟视无睹,必然造成学生知识基础薄弱,甚至学习热情减弱。若能以此为契机,将教学内容合理深化,便可收获显著的、优质的教学效果。
一、深化概念理解,筑牢知识基础
如果把数学知识的学习过程看作是在建造一栋大楼的话,那么,概念的学习就像是在为这栋大楼积累砖石。也就是说,理解概念是数学学习的基础性工程,必须做到深入到位,方能渗透于接下来的灵活性知识学习中,而不至于在复杂问题的干扰下偏离主线。高中数学中的基本概念看似刻板,但其中却蕴含着丰富的内涵,需要在理解时不断深化,将每一个概念掌握得准确到位。
例如,在对“集合”内容进行教学时,基本概念是学生接触到的第一个学习对象。我按照教材向大家介绍了相关概念之后,便请学生根据自己对集合概念的理解,解答如下问题:下列四个命题(1)设集合X={x|x>-1},则{0}∈X;(2)空集是任何集合的真子集;(3)集合A={y|y= }和B={x|y= }表示同一集合;(4)集合P={a,b},集合Q={b,a},则P=Q,其中正确的命题有几个?上述四个命题都是严格依据集合的基本概念范围来设置的,区别于单一的说教,是以具体的集合状态来反映概念。学生在解答这个问题时,必然要逐一判断命题的正误,从而在这些具体情况中深化对集合概念的理解。
概念学习是走进高中数学学习的第一步,这一步必须迈稳、走好。对于数学概念,绝不能停留在对其字面意思的知晓上,而要真正走到文字背后,感知其中所包含的内容。当然,仅靠学生自己是很难在第一时间将概念的内涵完全发掘出来的,这就需要教师的启发与引导,必要时还可以将概念理解的关键点明示出来,帮助学生将知识基础筑牢。
二、深化内容把握,鼓励变式思维
主体知识是课堂教学的关键,更是教学深化的重要着力点。当然,深化教学并不是一句空话,要落实到实际教学中来。“深化”一词所覆盖的行动范围很广,教师应如何具化和选择呢?在实际教学过程中,我经常会从思维变式入手,将具有代表性的问题不断进行深入挖掘与变化,并以之启发学生思路,引导他们更深层地理解知识。
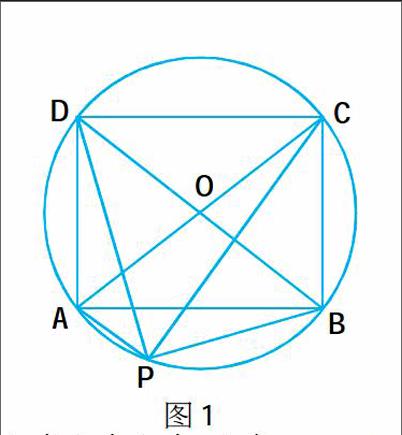
例如,在学习过“平面向量”的知识内容后,我为学生设计了这样一道习题:如图1所示,矩形ABCD内接于半径为r的圆O,点P是圆周上任意一点,求证:PA2+PB2+PC2+
PD2=8r2。学生运用向量的方法,通过表示出PA2= 2+OP2- · ,PB2=OB2=OP2- · ,PC2=OC2+OP2- · ,PD2=OD2+OP2- · ,并将上述各式相加,成功得证。接下来,我将这个问题变化成:已知△ABC中, = , = , = ,若 · = · = · ,求证:△ABC是正三角形。虽然在内容上和第一个问题截然不同,但学生似乎在解题思路和方法上并没有感到完全陌生。紧接着,我又继续提问:已知平行四边形ABCD的两条对角线AC与BD交于点E,点O是任意一点,求证: + + + = 。在这样的不断变式下,学生的思维也随之跳跃起来,对向量知识的运用也更加熟练了。
在题目变式的过程中,学生看到了同一知识内容的不同侧面与其所能达到的思考深度。相比教师的单方面讲述,这种形式显然生动有趣多了。将数学问题作为教学素材也是充分挖掘教学资源的重要举措。其实,在高中数学教学中,教师无须到课外过多地寻找拔高内容,只要着眼于教材,并将其中的问题进行变式处理即可,这既可以从问题本身进行变化,也可以从解题方法上开拓思路,让学生在知识认知过程中,虽起步于教材,却又能远远超越教材。
三、深化规律总结,寻找共性方法
为什么面对相同的知识内容,有的学生止步不前,有的学生却能应对自如呢?这就体现了学生在处理数学问题时的不同状态。我曾与不同学习状况的学生分别进行过交流,并对他们的学习方法和习惯加以观察,最终发现,能否找到不同问题之间的共性,并从中提炼出规律、方法并加以掌握和运用,这是决定学生数学学习效果的关键因素,这也是高中阶段数学教学的特点与精髓,更是进行教学深化的主要方向。
例如,在对“平面几何”内容研究过程中,学生遇到了这样一个问题:已知点P在抛物线y2=4x上,那么,点P到点Q(2,-1)的距离与点P到抛物线焦点的距离之和取得最小值时,点P的坐标是什么?如果仅从数字关系上推导,这道题的解答难度可不小。于是,我启发学生:“为何不把抛物线画出来看一看呢?”当大家将抛物线图象做出来之后,有的学生提出:“既然抛物线上的点到焦点的距离等于其到准线的距离,那么,这个问题是不是就可以转化为求两点之间距离的问题了呢?”图形一出,学生的解题思路也拓展开了。由此,学生切实体会到了图形对于数学解题的重要性,数形结合的思想也随之被学生自发地总结出来。
高中数学中的问题内容及形式数量繁多,其所对应的思想方法也是多种多样的。虽然运用这些规律性方法解决问题是高中数学学习的捷径,但教师一定要关注规律得出的方式。如果教师仅仅将一个个思想方法总结好教给学生,让他们像背课文一样地去死记硬背,这显然失去了数学学习的核心价值。教师要做的工作就是提供引导和思路,在解决问题的过程当中教会学生如何发现规律、提炼方法。如此一来,便给学生制作了一把有效应对各类知识的钥匙,无论学习内容如何变化,解题方法始终万变不离其宗。
四、深化学以致用,勤于联系实际
只有理论没有实践的学习是不完整的学习,这样所能得到的学习效果也必然是残缺的。特别是高中阶段的数学学习,知识内容愈发广泛,教师在指导实践中的连接点也愈发增多。如果在呈现理论的同时,加强联系实际,定可以为数学课堂呈现出全新面貌,让学生在学以致用中充分理解知识。
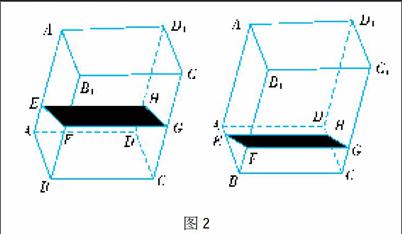
例如,在“立体几何”内容学习过程中,我曾请学生思考过这样一个问题:如图2左所示,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,固定容器一边BC于地面上,再将容器倾斜,随着倾斜度的不同,下列四个命题:(1)水的部分始终成棱柱状;(2)水面四边形EFGH的面积不改变;(3)棱A1D1始终与水面EFGH平行;(4)当容器倾斜如下图右时,EB·BF是定值,其中正确的是哪个?这个问题很好地将立体几何的理论性问题通过一个现实模型体现出来,学生边实操边思考,既有积极性,又有深入性,训练效果很好。
数学知识内容的内核在很大程度上是从应用角度体现出来的。可以说,将理论知识投入实际问题的解答中,这对理论学习本身就是一种检验和深化。与此同时,将实践元素充实到数学课堂中,可以很好地调节教学气氛,为学生带来新鲜具体的学习体验,对于高实效的高中数学教学追求来讲可谓一举两得。
优质的高中数学教学绝不能将教材内容视为教学对象的全部,而要将其作为一个基础性起点,源于之而高于之,将教材中的知识内容进行合理深化,引领学生更熟练地掌握知识。当然,对于这个深化的节奏,教师要科学巧妙地控制,深化速度不宜过快,否则会让学生感到应接不暇,反而使之产生更大的心理压力,甚至扰乱学生的既有思维秩序。只有将深化隐于无形,并融入平时教学中,这才是高中阶段所呼唤的常态性深化数学教学。
参考文献:
[1]段兆兵.课程资源的内涵与有效开发[J].课程·教材·教法,2003(3).
[2]吴刚平.课程资源的开发与利用[J].全球教育展望,2001(8).

