初中数学符号语言教学研究

刘小云

摘 要：初中阶段是数学符号语言学习的关键时期，研究初中数学符号语言教学对于提高学生数学学习成绩和培养学生数学思维具有重要意义。数学符号语言具有准确性、通用性、抽象性和简洁性的特点。目前，初中数学符号语言教学缺乏系统性、准确性，大多数都流于表面形式。在教学过程中运用多种教学手段，循序渐进地教学，使学生在灵活应用和理解的基础上加深记忆。

关键词：初中数学 符号 语言 教学 研究

数学符号是数学课程区别于其他课程教学的重要标志，它具有很强的准确性、概括性和抽象性。数学符号是数学学习过程中的重要数学语言，它把原先复杂的文字表述转变成了简便的数字语言。学生通过这些数学符号语言能够准确快速地理解数学题目中的相关信息，寻找到题目中的数学关系，提高数学解题的效率。

在2007年我国颁布的《全日制义务教育数学课程标准》中就提出了数学学习中“符号意识”和“数感”的概念，要求学生能够利用数学符号将数量之间的关系进行表示，使学生能够从具体抽象的语言表述中提取出内涵的数学符号，并能进行熟练运用与计算。

一、初中生学习数学符号语言的意义

初中阶段的学生在心理和认知方面都有较大发展，思维方式开始由具体形象思维向抽象逻辑思维转变，这是逻辑思维培养的关键期，也是学习数学符号的关键期。从学习内容上看，初中数学学习内容的重点开始由数学算数向数学代数转变，其中涉及了较多的数学符号语言，学生要能利用这些数学符号语言对数学问题进行推理和解答。这就要求学生不仅能理解数学符号语言的意思，还要能灵活运用。一方面，在初中阶段，学生对新鲜事物都有很强的好奇心和求知欲，这是学习数学符号语言的关键期，只有学好数学符号语言，才能为中学的数学学习打好基础。另一方面，数学符号的学习是初中生学习数学面临的一大障碍，原先的数学问题都是具体的算数，进入初中后则面临着大量的数学符号，使得很多学生无从下手，仅仅是对这些符号进行简单的机械记忆，往往会导致所学知识与符号表示之间存在严重的脱节。例如，在做题过程中，很多学生会因弄不明白符号所代表的隐含条件是什么而做错题；课堂上，由于学生对某些符号在理解上存在偏差而不明白教学内容。如果学生无法正确地理解和把握数学符号语言，就会对数学学习产生排斥心理，影响数学思维的形成。

二、初中数学符号语言的特点

1.数学符号语言具有准确性

数学学科的特点决定了数学符号语言的严谨性，数学符号所表示的数学公式和定理都做到了准确无误的表达。相反，数学符号语言表达的数学内容也是唯一的、准确的。例如，矩形的四个顶点为ABCD，那么就可以把这个矩形表示为 ABCD，那么，在这个数字符号描述下的矩形就是四个顶点依次为ABCD的矩形。

2.数学符号语言具有通用性

数学符号语言打破了国界语言的限制，它不同于人的语言在不同的地方有不同的种类，数学符号在世界各个国家表示的意思大都一样，具有一定的通用性，便于人们开展学术交流。另外，数学符号语言也适用于其他学科。

3.数学符号语言具有简洁性

数学符号语言不同于普通的语言描述，它具有很强的简洁性，它直接概括事物的本质，描述事物的本质属性。数学教学中利用数学符号语言能避免因过多文字描述而产生歧义的问题，减轻了数学学习思维的负担。

4.数学符号语言具有抽象性

数学学科的抽象性在很大程度上都体现在数学符号语言上，这是数学符号语言最为显著的特征。例如，l g100在平时生活中，它不能表示任何意义，只是一个简单的数字和字母而已，但在数学中，它表示的含义就是以10为底，100的对数。

三、初中数学语言符号的功能

1.便于学生形成解题思维

数学符号语言能够清晰地体现数学解题思路，便于学生掌握数学解题方法，使解题思维程序化。例如，学生在解题的过程中只要看到a2+2ab+b2的形式就会不自觉地套用配方公式。通过数学符号的形式能够使学生抛开复杂的文字阐述而直接抓住问题本质，易于学生把握和运用与数学相关的定理和概念来解题。

2.便于学生数学思维的培养

数学思维是人脑内部的数学活动，它通过具体的符号运算形式在人的头脑中体现出来。例如，两条直线相互垂直，那么一元二次方程的根和系数就会存在这样的关系，两根之和等于-b/a，两根之积等于c/a，不管计算的结果与过程如何，这些都是人们经过具体思维而得到的。

3.便于学生联想思维的产生

学生的联想离不开客观事物和经验，数学学科要获得较大发展，创造性思维必不可少。数学符号语言，是对现实事物的高度概括和浓缩，内涵信息容量非常丰富。学生看到相关的数学符号就会产生不同的联想，联想到符号所代表的事物以及它们之间的联系，从而发展学生的联想思维。

四、初中数学符号语言学习问题

1.学生对数学符号语言的掌握缺乏准确性

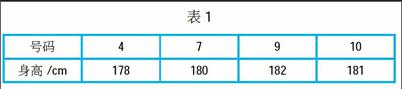
很多学生在学习数学符号所表示的公式和定理时，大多数采用先抄再背的方式来学习，这种急于求成的短时记忆方式，很容易导致记忆缺乏准确性。在平时教学中我发现，很多学生都面临着提取基本公式和定理困难的问题；有些学生看过题目后，感觉很眼熟，但却不知该如何下手解决。例如，下列各式中运算正确的有（ ）。A.（2x2）3=8x6 B.5a2b-2a2b=3 C.x6/x2=x3 D.（a-b）2=a2-b2很多学生对于幂的意义的把握并不很好，他们认为（2x2）3=2x6。再如，一道有关方差公式的考查试题：我县要举办一场篮球比赛，为了了解对手篮球队队员的状况，对他们的身高和号码做了如下统计（见表1），求这支队伍队员的身高方差？

这是一道典型的考查方差公式的题目，由于这一公式比较复杂，大多数学生学完之后就很少去理会它了，有的甚至连方差的概念是什么都不知道（平时练习题中对方差问题考查的较少），这是因为他们对相关的数学符号记忆不准确。

2.学生对数学符号语言的学习缺乏系统性

对于这方面的问题，主要体现在学生不能系统性地提取数学符号语言，尤其在涉及符号语言的综合类题目中。在平时做题中我发现，很多学生对于数学符号缺乏系统性的认识，如出现单一符号时，他们可能会灵光一现地发现其中的问题，但当多种符号同时出现在一个问题中时，他们就很难准确地提取出相关数学信息了，导致做题混乱。例如，已知A=a+3，B=a2-a+5，C=a2+5a-20，其中a>2，求证B-A>0，并指出AB和AC的大小关系，并求证。在解答这道问题时，仅有40%的学生完全做对了；有16%的学生在第一问中得到a2-2a+2后就不再继续往下做了；在第二问中得到a2+4a-21就不再往下继续做了；还有些学生在完成第一问，对第二问配方完成后就不再进行字母取值讨论了，这些都会导致做题错误。

3.学生对数学符号语言的理解流于表面

数学符号的意义在于它表示事物的本质内涵，而不是它的形式，但在学习过程中，很多学生对数学符号语言的学习和理解仅仅停留在它的形式上，而不能理解其本质。例如，已知一次函数y=3x-4k的图象与反比例函数y=（k-4）/x的图象相交，其中一个焦点的纵坐标为5，求这两个函数的解析式是多少？并求出关于x的不等式3x-3k<（k-4）/x。这道问题看似是一道函数问题，实际上是利用方程组和不等式来解决的综合问题。很多学生由于对数学符号语言的理解流于形式，往往解题无从下手；还有部分学生难以从原题中提取出函数图象的代数关系；有些学生在求出横坐标后，仅找出了不等式x<-2，却没有找到-4/3<

x<0这一隐含条件，这些都是学生对于数学符号语言的理解流于表面的体现。

五、结语

初中数学符号语言的学习不同于文科中一些知识的死记硬背，它需要循序渐进的过程，在灵活应用和理解的基础上加以记忆。因此，在教学中，教师要注意数学符号语言抽象与具体相结合，要从学生的实际生活出发，让学生体会从实际生活问题向数字符号转变的过程，不仅让学生知其然，还要让他们知其所以然。教师要通过不同的引导策略，以初中生的认知特点为基础，教师从基本公式和定理入手，培养学生学以致用的能力。同时，还要加强学生对于数学符号的学习与理解，在教授学生新的数学符号语言的同时，也要做好与已学数学符号语言之间的对接，为后续学习打下基础。教学中，教师可以利用比较法进行教学，比较前后数学符号语言之间的异同，达到温故知新、触类旁通的学习效果。

参考文献：

[1]曹校生.初中数学符号语言分类教学与实验研究[D].桂林：广西师范大学，2007.

[2]张文新.青少年发展心理学[M].济南：山东人民出版社，2011.