变“教学事故”为“教学故事”——从一道中考复习作图题谈起

江苏省江阴市云亭中学 徐联波

变“教学事故”为“教学故事”
——从一道中考复习作图题谈起

江苏省江阴市云亭中学 徐联波

新课程标准颁布后，广大数学教师在体现学生为主的“生本课堂”理念指导下，进行了很多思考与有益实践。什么是理想的“生本课堂”，叶澜教授曾作过这样精辟的论述：“课堂应是向求知方向挺进的旅程，随时都有可能发现意外的通道和美丽的图景，而不是一切都必须遵循固定路线而没有激情的行程。”数学课堂应该是由包括教师在内的许多灵动的生命体组成的动态过程，随时会有超出预设、鲜活丰富的即时生成性资源。如此动态的过程凸显的是师生之间、生生之间平等的“学习共同体”关系，“开放性”是其主要特征。笔者自实践学生讲题复习法以来，开放的数学课堂给足了学生自由展示的机会，一次次课堂预设外的“教学事故”演变成“教学故事”。结合2016年无锡中考22题，现将二轮复习时遇到的一道中考复习作图题产生的教学故事整理如下，以期交流。

一、题目呈现

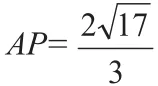
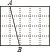
二、“教学事故”的发生

本题是2015年自贡市中考试题。二轮复习时，备课组将此题选入“尺规作图”专题，主要目的是培养学生利用网格设计作图，考虑转化为利用相似三角形对应边成比例的性质确定线段AB的三等分点。执教这节课时，我按惯例让学生主动上黑板讲解此题，学生围绕如何找到一条线段三等分点，给出了多种方法，完全超出备课组教师集体备课时的预设，课堂教学停于此题。在学习过程中，有些方法在其他同学听来好像不着边际，似懂非懂，我虽作补充解释，也显勉强。

三、“教学故事”的形成

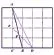
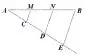
（2）构造三角形重心

连接AC、AD、CD得△ACD，由AB、DE为三角形的两条中线，交点为P为三角形的重心。则AP=2BP，即点P为线段AB的三等分点。

（3）根据平行线分线段成比例确定AB的三等分点。

过点A作射线，圆规在此射线上截取等长线段AC、CD、DE,连接BE，过点D、C分别作BE的平行线交线段AB于点M、N，即为所求作的三等分点。

四、“故事”的巧合

2016年无锡中考第22题，与上题有异曲同工之处：

如图，OA＝2，以点A为圆心、1为半径画⊙A与OA的延长线交于点C，过点A画OA的垂线，垂线与⊙A的一个交点为B，连BC。（1）线段BC的长等于______。（2）请在图中按下列要求逐一操作，并回答问题。

①以点______为圆心、以线段____ 的长为半径画弧，与射线BA交于点D，使线段OD的长等于；。请写出画法，并说明理由。

第（2）②题，若按方法1：（图1、图2）

过点O作OE⊥OC，且使OE=2AD,连接AE、OD相交于点P，或过点D作DE⊥AD，且使得OA=2DE,连接AE、OD相交于点P。

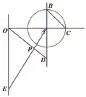
图1

图2

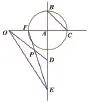
图3

若按方法2：（图3）

在直线AB上取点E，使得DE=AD，连接EF、OD，相交于点P。

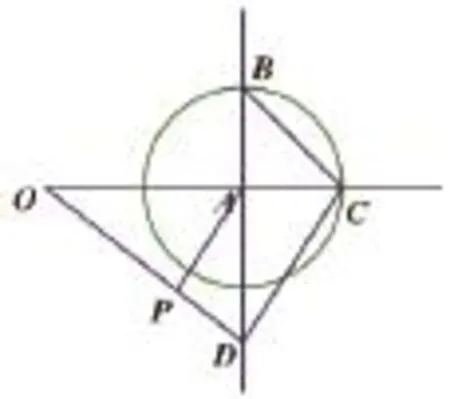
若按方法3：

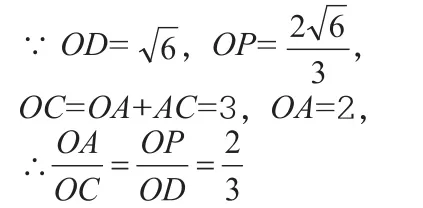
故作法如下：

连接CD，过点A作AP∥CD交OD于点P，P点即是所要找的点。

五、思考感悟

著名教育学家布鲁姆说：“人们无法预料到教学所产生的成果的全部范围，如今的课堂正显现出刚性向弹性转变的趋势，更关注过程和体验，关注过程和体验中即时生成的东西，在动态的生成过程中出新思想、新创意。”开放的数学课堂，学生参与课堂讲题的机会多了，预设之外的课堂即时生成，随时产生，有时甚至会出现影响课堂教学目标达成的“教学事故”。如果教师能抓住学生主动暴露思维的机会，不被课堂上的表象所迷惑，找出“事故”成因，就能让学生加深对题目本质的理解，加深对每个解法本质的理解，加深对所用概念、定理公式及相互联系的理解，这样的“教学事故”往往会变成教学效果明显的“教学故事”。