对二次函数中巧用轴对称性解决线段和最小值问题的一些思考
江苏省泗阳经济开发区学校 刘小艳
对二次函数中巧用轴对称性解决线段和最小值问题的一些思考
江苏省泗阳经济开发区学校 刘小艳
在苏科版八上《轴对称图形》一章中学习过利用轴对称性解决线段和差最值问题,尤其是最小值问题屡见不鲜,而二次函数中也常出现这类问题。在此,就利用轴对称性解决二次函数中线段和最值问题进行探讨。
一、两条线段之和的最小值
例1:如图,抛物线y=x2+bx+c与x轴交于点A、B,AB=2,与y轴交于点C,对称轴为直线x=2。

(1)求抛物线对应的函数表达式;
(2)设P为对称轴上一动点,求△APC周长的最小值;
分析:
(1)根据抛物线对称轴的定义易求A(1,0),B(3,0)。所以1、3是关于x的一元二次方程x2+bx+c=0的两根。由韦达定理易求b、c的值;
(2)如图,连接AC、BC,BC交对称轴于点P,连接PA。根据抛物线的对称性质得到PA=PB,则△APC的周长的最小值=AC+AP+PC=AC+BC,所以根据两点间的距离公式来求该三角形的周长的最小值即可;
解:(1)∵AB=2,对称轴为直线x=2。
∴点A的坐标是(1,0),点B的坐标是(3,0)。
∵抛物线y=x2+bx+c与x轴交于点A,B,
∴1、3是关于x的一元二次方程x2+bx+c=0的两根。
由韦达定理,得
1+3=-b,1×3=c,
∴b=-4,c=3,
∴抛物线的函数表达式为y=x2-4x+3;
(2)连接AC、BC,BC交对称轴于点P,连接PA。
由(1)知抛物线的函数表达式为y=x2-4x+3,A(1,0),B(3,0),
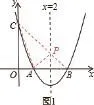

此时,PB+PC=BC。
二 、三条线段之和的最小值

(1)求抛物线的解析式。
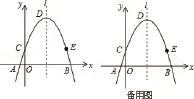
(2)抛物线的对称轴为l,与y轴的交点为C,顶点为D,点C关于l的对称点为E,是否存在x轴上的点M,y轴上的点N,使四边形DNME的周长最小?若存在,请画出图形(保留作图痕迹),并求出周长的最小值;若不存在,请说明理由。
分析:
(1)利用根与系数的关系得出α+β=,αβ=-2,进而代入求出m的值即可得出答案;
(2)利用轴对称求最短路线的方法,作点D关于y轴的对称点D',点E关于x轴的对称点E′,得出四边形DNME的周长最小为:D'E'+DE,进而利用勾股定理求出即可;
解:(1)由题意可得:α,β是方程-mx2+4x+2m=0的两根,由根与系数的关系可得,

解得:m=1,
故抛物线解析式为:y=-x2+4x+2;
(2)存在x轴上的点M,y轴上的点N,使得四边形DNME的周长最小,∵y=-x2+4x+2=-(x-2)2+6,∴抛物线的对称轴l为x=2,顶点D的坐标为:(2,6),又∵抛物线与y轴交点C的坐标为:(0,2),点E与点C关于l对称,∴E点坐标为:(4,2),
作点D关于y轴的对称点D′,点E关于x轴的对称点E',
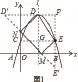
则D'的坐标为;(-2,6),E'坐标为:(4,-2),
连接D'E',交x轴于M,交y轴于N,
此时,四边形DNME的周长最小为:,如图1所示:延长交于一点F,在Rt△中,=8,

设对称轴l与CE交于点G,在Rt△DGE中,DG=4,EG=2,

由上面两个例题我们总结出一条规律:在二次函数中求线段和最小值时,可以把一条线段转换成与它对称的线段,从而利用两点之间线段最短求出线段和的最小值。

