例谈充分必要条件法解决数学问题的途径
江苏省启东市吕四中学 周 华
例谈充分必要条件法解决数学问题的途径
江苏省启东市吕四中学 周 华
侦探小说爱好者熟知千篇一律的情节,把怀疑的范围逐步缩小,最后侦探发现了罪犯。事实上,解数学题也存在着类似的情况,我们在解数学题时经常用到"充要条件"(即等价转化),但却很少注重“充分条件”和“必要条件”的应用,本文旨在通过几例说明“必要条件”在解题中的应用,先求出使得命题成立的“必要条件”,再由题设进一步求出使得命题成立的“充要条件”,从而解决问题。
必要条件;充要条件;定义域;充分条件;等价转化
我们在平常的教学中可以看到,大部分学生对充分条件和必要条件的理解普遍感到十分困难,抓不住它的本质。虽然江苏省高考数学考试说明中对这部分内容的要求不是太高,但它作为一种数学的解题思想,对培养学生理解问题和解决问题的能力是有很大用处的。
定义2:理解“充分”,“必要”词语的含义并定性地判断关系。“充分”相当于“有我便已足够,无需其他”;“必要”相当于“没它不行,但唯有它也未必行”。
众所周知,等价转化思想是一种重要的数学思想,在解题中的作用往往体现在化复杂为简单,化陌生为熟悉,并且通过等价转化得到的结论是不需要检验的。
但在数学解题中,有很多情形不易、不宜,甚至是不可能进行等价转化,这时只有“退而求其次”,可以考虑用非等价转化的方法来解题,常见的方法有“先必要后充分”和“先充分再必要”,本文主要谈谈先找出使结论成立的必要条件,然后再验证其充分性。
一、运用充分必要条件法解决数列与不等式的综合问题
数列是高中数学的一个重要的内容,也是历年高考、竞赛的常见题型,近几年江苏高考题很喜欢把数列定义成为压轴题,用来拉开分数,选拔人才。呈现递推关系的综合性试题,特别是与不等式的综合是教学的难点,往往入手比较困难,不容易想到解题思路,有时还会出现运算量比较大的情况,所以在此类问题中巧妙运用充分必要条件的解题思想往往会给解题带来方便。

这个不等式不能解,如果硬做,只能通过取值一个一个进行尝试可以得到答案,但是需要花的时间太长,在考试时很难算到答案。

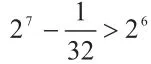
故可以判断最大正整数n的值为12。
评注:此类问题,若按数列的基本思路循规蹈矩,即用等比数列的通项公式求出这个数列的通项公式代入不等式两边,然后解不等式。思路简单、清晰,学生容易上手,但由于化简得到的不等式较大,属于不可解的不等式,代入检验的运算过程复杂,计算量大,需要学生有足够的耐心和细心,一般学生很难解到最终的结果(具体解法略),但若能找到其必要条件把它配成可以解的不等式也许能很快找到结论。
二、运用充分必要条件解决含参数不等式恒成立问题
函数的基础性强,特征性明显,是高中数学教材中非常重要的部分,也是学生普遍觉得比较头疼的问题。习题中对函数的考查也是必不可少的,而函数的单调性,有关函数的不等式恒成立问题是考查的一个重点和热点内容。我们平常接触的解决含有参数不等式恒成立的问题大概分成如下几种:1.分离参数转化为最值问题;2.直接转化为最值问题;3.数形结合法。以上三种解法是几种常用的基本方法,但是有些题目因为分离参数之后的函数表达式太大,导致到后面最值求不出来,从而得不到最终的结论。但如果能找到不等式成立的必要条件探索出参数的值,然后验证其充分性也许会事半功倍。
(1)求函数f(x)的单调区间。
(2)若a=1,k为整数,且当x>0时,,求k的最大值。
当a≤0,函数f(x)的增区间为(-∞,+∞)。
当a>0函数f(x)的减区间为(-∞,lna),增区间为(lna,+∞)。
(2)当a=1,。 得到,代入不等式
这个时候直接求函数的最小值比较困难,转而先找不等式恒成立的必要条件:
不等式对于x=1恒成立
然后验证当k=2,在x>0恒成立。

利用导数,可得函数g(x)在(0,1)为增函数,在(1,+∞)为减函数。
所以k=2,在x>0恒成立。所以k的最大值为2。
评注:此类问题,用导数求解一类参数取值范围或最值的问题在高考中很常见,而本题用常规的等价转化即分离常数再求相应函数的最值难以求解,而解答方法——“先必要后充分”是一种容易掌握的好方法。函数导数的大题往往放在最后两个题中,如果能够掌握这种方法,就可以在高考中取得明显的优势。
化归与转化思想是数学中重要的思想方法之一,也是高考重点考查的方法之一。而大多数考题或者是大家的解题习惯多是实施等价转化,即寻找题目求解的充要条件,很少涉及不等价转化。以上几道例题都有一定难度,而善于利用寻找必要条件,可以达到化繁为简,化难为易,避免了分类讨论,实现大题小做。因此,利用必要条件解题,可以缩小参数范围,开阔解题思路,优化解题过程,提高学生的数学思维能力。

