激活深度思维:小学数学题组开发的核心要义
江苏省苏州市吴江区盛泽实验小学 杨伟琴
激活深度思维:小学数学题组开发的核心要义
江苏省苏州市吴江区盛泽实验小学 杨伟琴
数学世界是一个思维的世界。数学教育的任务是“形成和发展学生的具有思维特点的智力活动结构”,因而,数学教学不但要向学生传授知识,而且要培养数学能力,特别是发展学生的思维能力。在儿童数学教与学的过程中,教师可以从教材习题入手,进行合理挖掘,设计题组,激活儿童的深度思维。
数学题组;儿童思维
思维是在社会实践中产生的,是在表象、概念的基础上进行分析、综合、判断、推理等认识活动的过程,是人类特有的一种精神活动。数学世界是一个思维的世界。数学教育的任务是“形成和发展学生的具有思维特点的智力活动结构”,因而,数学教学不但要向学生传授知识,而且要培养数学能力,特别是发展学生的思维能力。因此,现代教学论已经把数学教学目的提到了“知识——能力——思维”的高度。
在儿童数学教与学的过程中,教师每天立足课堂行走于教材与学生中,教学方式在不断地改变,教育教学理念在不断地更新与提升,但教材研读仍是教师们的薄弱环节,很多教师不愿花时间与精力翻看教学参考书籍,不愿深入解读教材中的例题及习题的编排特点,不能从整体上去认识、把控教材,更不能结合学生的年龄特点与已有知识去重组题目、开发题目。这样的儿童数学学习过程很容易造成儿童认知结构的脱节与断裂,造成儿童思维的单一、松散。这就需要教师在平时的数学教学过程中时常关注并有意识地培养学生的思维能力,着力于发展学生的发散思维、转化思维、系统思维、逆向思维、对应思维等。怎样培养呢?从教材编排的习题入手,通过变式、重组、联想、拓展等方式对题目进行有针对性的开发,借助题组激活儿童的深度思维,让题组学习成为发展儿童思维的数学学习之旅。
一、存同求异:对比性题组叩启求异思维
求异思维是在指在固有思维方式、思维习惯的基础上,另辟蹊径,从新的思维角度去思考问题、分析问题的一种思维。它具有流畅性、变通性和创造性的特征。在数学教学中,可以用对比性的题组叩启儿童的求异思维。如在一年级下册学习“100以内的进位加法”之后,我结合教材上第87页第6题改编了这样一题组:每组中哪道算式的得数大?
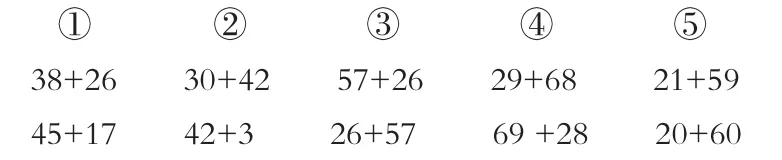
在平时的教学中,遇到比较大小的题目,时常会引导学生们先分析算式的特点,再根据特点灵活选用算、估、比的方法进行思考。算,就是先计算出得数,再根据得数的大小进行判断;估,就是先估算出得数是几十,再根据估算结果进行判断;比,就是根据算式间的联系不计算直接判断。由于学生所处的文化环境、家庭背景和自身思维方式、接受能力的不同,学生获得的学习经验也不同,面对相同的题组,学生们选择的思维角度、思维方式不同,思维的深度也不同。在此题组中,除第①题思维基本是固定外,其余四题的思考方法不唯一,不同方法间的思维深度相差很大。因而,交流时在肯定算倡导估的基础上,引导及鼓励儿童从不同角度寻找关系进行对比思考,说出自己独特的见解,在思维碰撞中叩启求异思维,把思维引向深层次。如:第③组算式中的两个加数大小是一样的,只是位置不同,交换两个加数的位置,和不变(也就是以后要学的加法交换律)。第④组可迁移第③组的知识经验,交换两个加数十位上数的大小,和不变;也可以根据29→69大40,68→28小40,一个加数大40,另一个加数小40,和不变。第⑤组迁移第④组的知识,21→20小1,59→60大1,一个加数小1,一个加数大1,和不变,同时也把两位数加两位数的计算转化成整十数加整十数的计算。
经此课后,我发现虽然是计算课,但只要用设计好的对比性题组进行教学,同中求异、异种求同,儿童的数学思维就会很活跃,很发散。
二、化繁为简:变式性题组叩响转化思维
在稍复杂的分数实际应用问题的条件中,经常会出现两个或两个以上的单位“1”的量,从属于不同单位“1”的分率,就很难分析、比较以确定他们之间的关系。运用转化思维的方法,就可以将不通单位“1”的分率转化为一个统一单位“1”的分率,也可以将分数问题转化成比、比例的问题,经过转化后的数量关系以及量率关系就由复杂转化为简单,由隐蔽转化为明显,为正确的解题思路的形成创造了必要的条件。结合教材中的习题,我设计了以下题组:
1.学校合唱组有60人,其中男生人数是女生人数的1/4。男生有多少人?
2.甲的年龄比乙的年龄少1/6,乙的年龄比丙的年龄多1/3,甲比丙大4岁。丙几岁?
3.甲乙两人共存书若干本,已知甲存书本数的1/4等于乙存书本数的1/5,又知乙比甲多存了24本。甲乙各存多少本?
这三道稍复杂的分数问题,都是由简单的分数问题变式而成的,单位“1”的量在增加,数量关系在变复杂,题目也由易逐渐变难。如果用原有的思维进行分析思考,困难较大,但如果根据分数、比、除法的关系,把分数问题转化成比、按比例分配的问题,就简单多了。解答第一题时,教师要引导学生对“男生人数是女生的1/4”进行多样化的转化,如转化成:男生人数是总人数的1/5,女生人数是总人数的4/5,男生人数与女生的比是1∶4,女生人数是男生人数的4倍,男生人数比女生少3/4……”然后选择自己喜欢的、简单的数量关系进行解答。解答第二题时,借助第一题生成的转化经验,把“甲的年龄比乙的年龄少1/6,乙的年龄比丙的年龄多1/3,”转化成“甲与乙的年龄比为5:6,乙与丙的年龄比为4:3”,再根据比的基本性质得到“甲与乙的年龄比5:6=10:12,乙与丙的年龄比4:3=12:9”,从而得出甲:乙:丙=10:12:9,甲:丙=10:9,甲比丙大4岁,丙就是4×9=36岁。而在解答第三题时,教师既可引导学生用比例的知识把“甲存书本数的1/4等于乙存书本数的1/5”转化成甲存书本数与乙存书本数的比是4:5,也可用分数的知识把甲存书的本数看作单位“1”,乙存书的本数就是甲的(1/4÷1/5),这样就转化了单位“1”,把两个不同的单位“1”转化成一个单位“1”,就可以直接分析比较解答了。
转化是数学中最常用的思想。其精髓在于将未知的、陌生的、复杂的问题通过演绎归纳转化为已知的、熟悉的、简单的问题。在这里借助变式的题组,把复杂的分数问题转化成简单的分数问题,转化成比的问题,转化成按比例分配的问题,使儿童的思维更灵活,更深入。
三、以点到面:联想性题组叩建系统思维
儿童数学的教与学,每一堂课、每一个内容的学习应该是集整体感与系统思维为一体的过程。系统思维就是对事情有一个整体而全面的思考,对事情或问题的产生、展开、发展以及问题的解决、结论的获得及在这个过程中方法的运用、优化和对未来的影响等一系列问题作为一个整体系统来研究和进行综合地考察认识的一种思维方法。
儿童数学学习的内容是由浅入深,由易到难,由简到繁,循序渐进的,与此同时也在客观上造成了所有知识都是凌乱摆放的。教师要引导学生在数学学习过程中边学习边提炼加工,理清知识之间的纵横联系,构建知识体系。如在一年级下册的总复习中,我以教材第96页的第7题为突破口,以点到面,构建100以内加减法中不同类型算式的结构体系,叩建学生的系统思维。教师先要求学生各自计算,再比较三题间的联系与区别,而后引导学生说说由“55+30、55+3、55+8”这三道加法算式想到了学过的哪些加法算式?说说由“55-30、55-3、55-8”这三道减法算式想到了学过的哪些减法算式?然后每位学生各自找题整理100以内的加减计算。在交流展示时发现,虽然学生们选择的题目,先后顺序不同,但类型很完整,把学过的100以内的加法(减法)类型全部囊括在内,其中有几位学生的整理十分系统。如:加法:5+3 5+8 50+3 55+3 55+8 50+30 55+30 55+33 55+38。 减 法: 5-3 15-8 50-3 55-30 55-8 50-30 55-30 55-33 55-38。
学习是基于儿童原有知识经验基础上的自我建构,儿童头脑中的知识结构构建得越好就越利于保存和利用。儿童数学教学的路上,需要联想,需要用系统思维自主构建知识链,融会贯通知识网。
数学课堂教学,是数学本质的教学;数学题组教学,是数学思维的教学。在以后的教学中,我会一如既往地关注题组,开发题组,用题组激活儿童深度思维。
——例谈“体积、容积单位换算”教学

