高中数学课堂有效提问的探索
江苏省海门实验学校 周英亮
高中数学课堂有效提问的探索
江苏省海门实验学校 周英亮
问题是数学课堂教学中教师用于启发引导学生思考、促进学生展开探究活动的重要方式,问题是否有效将直接影响数学课堂教学效率。结合高中数学课堂教学中提问实践来看,问题过于突兀,缺少情境承托,致使学生对问题无法产生兴趣,很容易造成“自问自答”的现象。同时,提问后对学生的讨论组织不够,也会影响问题的解答。当然,学生讨论问题后,教师还要给予学生点拨和指导,这样才利于问题的解决。
一、以“境”引问,激发学生探究兴趣
在数学教学中有大量的概念、公式、定理等,这些知识是对事物特点的抽象性概括,故而具有抽象性特点,学生在学习这些知识过程中,需要以一定的直观形象素材作为过渡。如“空间几何体”的教学中需要借助如水立方、鸟巢等建筑物来引导学生观察,在观察中对棱柱、棱锥、棱台等具有几何结构的物体形成感知。但教学中太注重形式,于是,在图片选择、呈现方式上追求花哨而没有注重以问题作为引导。
不可否认,在教学中以情境促进学生直观感知,再以问题启发学生思考,这样效果才会更好,但要分清形式和作用之间的关系,要注重在情境中通过问题去引导学生思考,启发学生进入探究活动。如在“抽样调查”教学中,以某企业生产产品后算其合格率为案例,由此而引出大量的数据,那么,针对这些数据,该怎样调查,是否全面,在复习样本概念的基础上追问学生如何从总体中抽取样本,然后引出简单随机抽样的概念。又如“指数函数”的教学中,先以“非典”事例而引出某细菌的分裂方式,由此而设分裂次数为x,细胞数目为y,引导学生得到函数关系式y=2x。再以走路的故事引导学生得到函数关系式y=(1/2)x。此时引导学生观察上述的函数关系式,看看有什么特点,由此而得到底数大于0且不同,指数均为x,教师再抛出指数函数的概念,这就利用学生理解该函数的概念。
二、以“问”导学,促进学生合作探究
在实践中,因问题设计没有紧扣目标展开,故而虽然课堂中学生也在积极参与问题互动,但效果始终不佳。在教学中提出问题,目的就是要让学生通过问题的探究而达成目标,故而问题和目标是环环相扣的。一旦探究中的问题脱离了目标,学生的探究活动会显得盲目,在解决问题过程中,虽然学生努力解决了教师所提的问题,但因问题和目标之间的脱节,探究活动自然也就难以达成目标。在教学中,教师提出问题的目的是为了让学生在问题探究过程中获得知识构建,那么,问题就应该是紧随目标而提出的,也正是因此,在设计问题时,教师要充分考虑当次课堂教学的目标,这样才能根据目标而逐层提出问题引导学生展开探究活动。
问题设计要能突出知识目标,能让学生在问题探究过程中掌握相应的知识点。如在“倾斜角与斜率”的教学中,重点是要让学生在探究中掌握直线的倾斜角和斜率的定义。教学中先给出图1并提问:过P的一条在直线绕P点旋转,不管旋转多少周,它对X轴的相对位置有哪些情形?既然过两点能确定一条直线,能否确定过P点的直线L的位置?它们之间又什么联系?接着追问“怎样描述直线的倾斜程度?”以图2引导学生标出直线的倾斜角并问其哪一条违背了定义。接着继续提问题“直线倾斜角是否能为0°,能否是锐角?直角?钝角?平角?大于平角?正切函数的定义域是什么?任何直线都有斜率吗?如果已经知道直线上的两点坐标,如何求其倾斜角和斜率?”在对这些问题的讨论上而总结出倾斜角的概念。在提问过程中还需注意,课堂是在不断发展的,问题要紧扣目标而层次性地展开,要让学生在解决前一问题的基础上去解决新的问题,以此而让学生深入到知识内部中。

三、以“讲”促学,帮助学生构建知识
提出问题引导学生探究,目的是要让学生从被动接受的学习方式转变到探究中,在主动参与中去合作(同桌交流和小组交流讨论),去完成问题的分析,或对知识点进行共同分析、辩论,在共同探究中更好地去理解知识点。但从课堂实践中不难发现,很多教师更注重探究的结果,而对过程不太关注。以问题作为引导,让学生在问题的引导下展开谈论交流活动,教师在学生讨论交流的过程中给予学生指导,针对学生的讨论和学生形成互动,在互动中帮助学生理解新知,以讲解、点拨等方式来突出重点,这样更利于学生主动去获得知识,摆脱被动接受的学习方式。
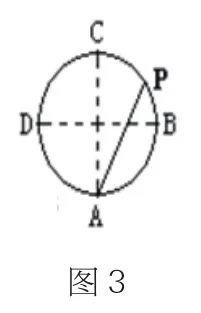
注重探究过程,就是要让学生能积极经历知识的构建过程,在这个过程中,教师要善于利用各种活动、任务、活动等方式而对学生实施引导。如“三角函数的周期性”的教学中,对于周期学生都不太陌生,要让学生能建立起函数周期性的概念,教学中就需引导学生围绕三角函数而进行讨论。首先,出示图3引导学生分析点P的运动轨迹而直观感知其周期性,如果P到A的距离为y,运动时间为t,那么y是t的函数该怎么表示,(圆的半径为2,每4分钟运动一周)讨论得到y=f(t),此时教师指出f(0)=f(4)=f(8)=f(12)=……=0,(位置在A点),f(2)=f(6)=f(10)=f(14)=……=4,(位置在C点),不难看出P运行到t分钟和(t+4)的位置是相同的,于是自然可得到f(t+4)=f(t)。那么,f(t+8)、f(t+12)与f(t)有什么关系?此时引导学生交流并说明其意义。教师根据学生的表达并用描点法画出图象,得到在区间(0,4)(4,8)(8,12)……内重复的结论。在此基础上引导学生对函数的周期性定义进行概括,教师再点拨。如此,对于概念,并不是教师直接告诉学生,然后让其以机械的方式去记忆,而是在探究活动中明确其内涵,引导学生总结,通过过程而得到结果。让学生经历其过程,内化知识,形成体验。
在高中数学教学中,“问”并不是教师的单向活动,而是教师和学生之间的互动活动。在数学课堂教学实践中,要关注学生的兴趣特点,以“境”来引入问题,以问题引导学生展开探究活动,辅以教师的点拨和指导,让学生经历数学知识的形成过程,这样的问题才会更加有效。