优化习题课教学模式，追求高效课堂

江苏省太仓市第一中学 陆春霞

优化习题课教学模式，追求高效课堂

江苏省太仓市第一中学 陆春霞

在数学课堂教学实践中，与新授课相比，习题课教学有时会出现这样尴尬的一幕：老师在课堂上讲得激情澎湃而学生却是无精打采、目光呆滞，课堂效率低。如何才能在数学习题课上调动起学生的积极性、发挥学生的学习主动性？唯有优化习题课教学模式，才能激发学生的内部学习动力，提高习题课的效率，创建高效课堂。

一、积极探讨——简化图形，回归本源

新型的教学模式，不妨将课堂交给学生，让他们自己去上他们的习题课，每个人都去做老师，那样的话，每个学生都有可能被叫到，效果会比老师讲好得多。具体应该如何操作？主要总结为以下几点：

首先，由学生来担当主讲的角色。但讲课的内容需要老师来确定，也就是说，老师必须准确地选择学生力所能及而又不能完全掌握的范围，并且把选好的题目以课后作业的形式留给学生，给他们充分准备的时间。其次，在课前师生可以相互交流，也可以让同学之间进行合作讨论，由老师去解决学生在讨论过程中解决不了的问题。最后，在习题课上，老师完全把讲台交给学生，由他们来充当教师的角色，只是在一些模糊和没有讲清楚的地方由老师来补充讲解。

例如，在《三角形相似》的习题课中，有这样一题：如图，正方形ABCD和正方形CEFG各有两个顶点在坐标轴上，其中A（0，1），B（2，0），E、F两点同在x轴上，双曲线y＝（k＞0）经过边AD的中点P和边CE的一点Q。

（1）求该双曲线所表示的函数关系式；

（2）探索点Q是否恰为CE的中点？请说明理由。

这道是考试题，考试时，有好多学生都做错了。课后经过讨论，很多同学已经有了思路。在课上，学生甲：第一小问，过点P作轴，利用K字型，△APH∽△BAO，并且相似比AP∶AB=1∶2，可以算出AH，PH的长度，进而可以求出P的坐标。

学生乙：第二小问也是根据K字型，△ABO≌△BCE，可以求出BE=1，CE=2，进而求Q的坐标，-，所以Q不是CE的中点。

教师及时归纳，解决此类问题可以从图形特征入手，体验K字型这个基本图形在题目中的广泛应用，加深对此类图形特征的理解，提高解决问题的综合能力。

在这种模式实施了一段时间，就有同学主动要求上台讲课，因为看见自己的同学个个上台讲解自己独到的解题方法，让同学们有了竞争的心理，别人可以，自己为什么不可以，就连刚开始因胆怯拒绝上台的同学也开始跃跃欲试。

二、开放研讨——深化思维，积累经验

众所周知，在致力于解决问题的习题课中，我们的一个主要的目的就是开拓学生的思维方式，让学生的解题能力有所提高。很多老师提议，我们可以采用变式教学，这是习题课的法宝之一。但这是由老师查找资料，加工之后呈现在学生面前的，学生被动地接受。老师应该想方设法提供这样的机会，给学生一道条件不完整的题，让学生自己加条件，解答题目。

例如，在《三角形相似》的习题课中，有这样一题：矩形ABCD置于如图所示的平面直角坐标系中，点F在线段CD（C，D除外）上运动，连接AF，将△ADF沿AF折叠，点D的对应点为点E，AB=6，AD=10，若F的坐标为________，求点E的坐标。（要求先补全题目，再求点E坐标）

这道题目是开放式题，答案不唯一，到底分几种类型？

老师先引导学生思考，然后就会有学生发现本题的关键点是分点D的对应点E在矩形内，边BC上，还是在矩形外三类。

学生甲：点D的对应点E在BC上，利用△ABE∽△ECF，可以求出E，F的坐标。

学生乙：还可以利用勾股定理，设CF=x，DF=FE=6-x，

解方程可以算出CF的值，从而求出E，F的坐标。

学生丙：点D的对应点E在矩形内，过E作X轴的平行线交Y轴于点P，交CD于点Q，利用K字形证△APE∽△EQF，可以求出E点坐标。

学生丁：点D的对应点E在矩形外，同样的方法利用K字形相似也能求出E点坐标来。

教师及时归纳，通过寻求E点的位置变化规律，引导学生继续深入思考点E的位置变化引起的三角形AEF的面积变化，进一步探究面积的最大值或最小值问题。通过折纸“做数学”的过程，让学生更有直观的体验和感受。

这样，就把被动的变式教学改变成有趣的专题研讨。实践证明，很多学生是很有这样的能力的。如果有的同学陷入僵局，那么再让学生自己思索一遍，进行梳理，并及时反思，最后回顾一遍做题过程与关键性的地方。

三、自助学习——提炼方法，形成通法

这是一种最为灵活的授课方式，适合用于大型考试之前。这个时候学生需要大量的时间进行复习，上课时可根据自己的问题自行复习，有问题时先小组内讨论解答，解答不了请别的小组帮忙，老师再帮助补充。

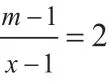
本题是学生甲（一位数学成绩中等偏下的同学提出的），小组里学生乙马上就给出了帮助，他指出学生甲没考虑去掉增根的情况。

本题力求向学生展示一个较完整的分式方程知识体系，进一步促进学生对分式方程增根的理解，达到“以小见大，以点带面”的复习效果。

再如，如图，已知在△ABC中，BA=BC=20cm，AC=30cm，点P从A点出发，沿AB以4cm/s的速度向点B运动；同时点R从C点出发，沿CA以3cm/s的速度向A点运动，设运动时间为x，△APR能否与△CRB相似，若能，求出AP的长，若不能，请说明理由。

这道题是一位中等生提出的，另一个小组的学生丙给予了帮助，他指出本题应分类讨论，条件BA=BC，所以∠A=∠C，故本题只需分△APR∽△CRB与△APR∽△CBR两类即可。

教师及时归纳，解决动点问题的基本思路是：①理解动点运动的基本要素（方向，速度，路径）；②分析运动后，变量与常量的数量关系；③构造几何模型寻求等量关系；④回归实际问题情境，对解进行合理性存在性检验。

不断优化习题课教学模式，创建高效的课堂是每一位老师毕生研究的课题之一。灵活多样的习题课教学模式，既减轻了学生的负担，同时也减轻了教师的工作压力，真正把学习的自主权还给学生，引导他们自己去探索，使他们真正成为学习的主人。