概率和统计的几点思考

江苏省仪征市马集中学 夏玉荣

概率和统计的几点思考

江苏省仪征市马集中学 夏玉荣

概率统计在日常生活有广泛的应用，概率统计观念的形成有赖于经历概率统计活动的过程。新课程中，对概率统计意识和用数据来说话的理念非常重视，因此，考试中加强概率统计内容和概率统计观念的考查已成不可逆转的趋势。

新课程改革实施以后，“统计”不再当作“代数”课程中的一个学习内容和一个基本知识点，而是形成了自我完善、自我独立的一个知识体系和知识板块，并且所学内容也不再是“统计初步”，而是有了较为全面系统的统计知识内容，同时学习“统计”也不再是一般意义上的笼统的计算或术语概念的记忆，而是要让学生了解和掌握基本的统计思想、统计方法，准确理解统计概念的现实意义，迅速树立起统计思想，用统计的结果指导我们的工作，服务于我们的生活；而“概率”是第一次展现在初中学生的面前，是高中学习内容的下移，它的出现是对学生确定结果下的思考方式和思维方法的颠覆，是对不确定结果下的随机现象的深度认识，是将结果的随机性和频率的稳定性的有机统一，是不确定的现象和可以确定的趋势的科学整合，“随机而不随便”。努力增强学生的随机观念，初步掌握用确定的方法分析不确定的现象。

一、题面丰富，题型多样，考点全面，分值加重

细阅全国各地中考试题，“统计与概率”部分的考查既做到内容全面，又能保证重点突出。统计部分主要有：数据收集方式的选择和确定、数据统计图表的选择和绘制、数据分析概念的理解和运用以及根据数据分析的结果进行的评估和决策。概率部分主要有：事件的识别、可能性大小的判断、概率本质的理解、频率与概率的估计、利用树状图或列表格的方式分析简单的随机现象中的可能事件数和发生数，从而求出概率值、以及通过实验或模拟实验的方法估计一些较为复杂事件发生的概率，几乎每个知识点都可以成为考查的内容，但解答题又主要以统计图表的分析理解和应用为主要方向，概率又几乎不变地以图表分析计算概率为主要目的。

（2016·广西百色）为了了解某班同学一周的课外阅读量，任选班上15名同学进行调查，统计如表，则下列说法错误的是（ ）

阅读量（单位：本/周） 0 1 2 3 4人数（单位：人） 1 4 6 2 2

A.中位数是2 B.平均数是2 C.众数是2 D.极差是2

评注：本题是以生活素材为背景，以表格的形式给出信息，既考查了学生的统计意识，对相关统计量所代表数据特征的理解，又便于区分多个统计量在实际生活中的应用 。

（2016·湖北随州）为了响应学校“书香校园”建设，阳光班的同学们积极捐书，其中宏志学习小组的同学捐书册数分别是：5，7，x，3，4，6.已知他们平均每人捐5本，则这组数据的众数、中位数和方差分别是（ ）

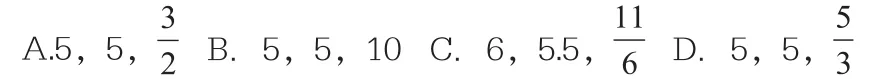
评注：本题集中考查了“三数”的概念，数据很少也很简单，但对统计概念理解的要求却一点也没有降低，更重要的是在这道填空题中竞有意地考察了一种数学思想－－分类思想，使“四基”的考查落到了实处。

二、基础突出，理解侧重，应用强化，能力发展

所谓突出基础，可以从两个方面得到验证，一是考查的内容的全面性可以体现（前面已做了说明），二是难度控制得很低（尤其是填空题和选择题，基本在“了解”、“理解”的目标层面），得分率较高。

所谓侧重理解，就是说对统计与概率的相关概念的考查，不是以记忆和计算为主要目的，而是要求考生在准确理解概念本质的基础上进行选择和判断。

所谓强化应用，一是数学学科本身的学习功能所致，二是检查学生能力的需求。要通过观察、比较、综合等方式考查学生的读图、释图、作图和评图的能力；要通过统计图表和统计量考查决策推断能力；要通过结合实际问题背景和问题的表征形式，考查计算简单随机事件概率的能力。

（2016·山东省东营市）“校园安全”受到全社会的广泛关注，东营市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题：

（1）接受问卷调查的学生共有_______人，扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°；

（2）请补全条形统计图；

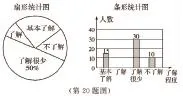
（3）若该中学共有学生900人，请根据上述调查结果，估计该中学学生中对校园安全知识 达到“了解”和“基本了解”程度的总人数。

评注：本题以校园安全为背景，以扇形统计图和表格的形式呈现问题，既考查了学生从单张统计图中获取所需信息，又考查了学生综合利用两张统计图表处理信息的能力，另外，还考查了用样本估计总体、从特殊到一般的数学思想。试题编制采取了层层递进、环环相扣的策略，有助于考查学生的探究能力。同时，对我们的教学也释放一个信号：在单一知识点的教学中要注重知识间的联系、整合及数学思想的渗透。

三、方法考查，思想渗透，文化传播，素质提升

数学思想是数学的精髓，是培养学生数学思维能力的重要环节，数学思想是对数学知识与方法规律性的理性认识，是解决问题的根本策略。“统计与概率”中的数学思想可分为特有的数学思想和一般的数学思想，其中特有的数学思想主要是随机思想、统计调查思想、统计描述思想、统计推断思想等，一般的数学思想主要有方程思想、数形结合思想、分类讨论思想、函数建模思想、整体代换思想、等价转化思想等等。

评注：本题主要考查了学生一元一次不等式解应用题的能力。要求学生从一元一次不等式组集中获取信息，并分析问题，用数字说话，而不只是停留在观察层面上，这对于培养学生的科学态度，了解不同领域内容都是很有益处的。

最后，我们要知道统计与概率知识是每一个人的必备常识和基础，所以，在教学中一定加强重视，强调其中的知识在社会生活和科学领域中的应用，注重学生的探索和合作交流，注意教学模式和动手实验，不要把统计内容处理成纯计算的内容。